2021-2022学年八年级数学人教版下册17.1.2利用勾股定理解决简单的实际问题课件
文档属性
| 名称 | 2021-2022学年八年级数学人教版下册17.1.2利用勾股定理解决简单的实际问题课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
这就是本届大会会徽的图案.
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智。它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽。
把勾股定理送到外星
球,与外星人进行数学交流 !
——华罗庚
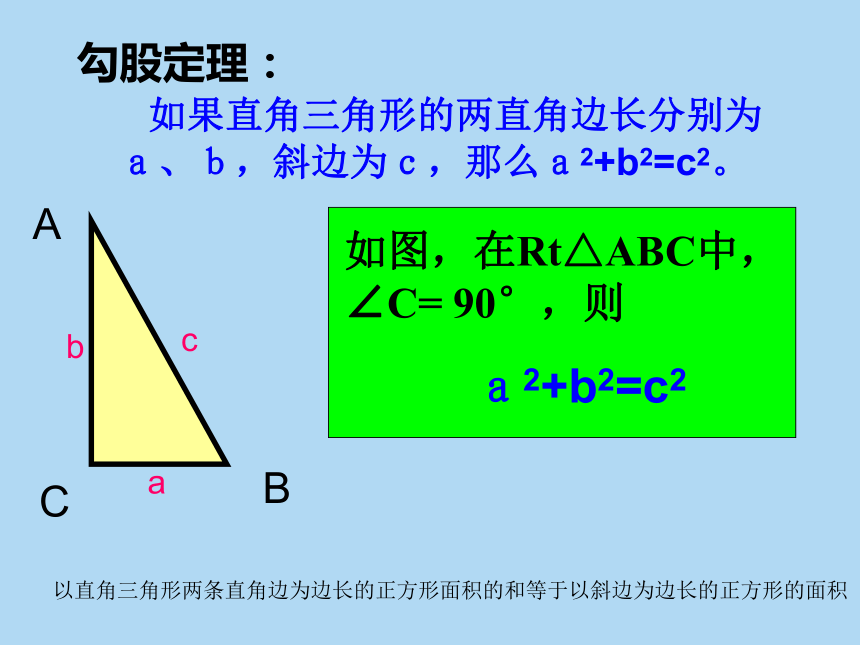
勾股定理:
如果直角三角形的两直角边长分别为
a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2
A
B
C
a
c
b
以直角三角形两条直角边为边长的正方形面积的和等于以斜边为边长的正方形的面积
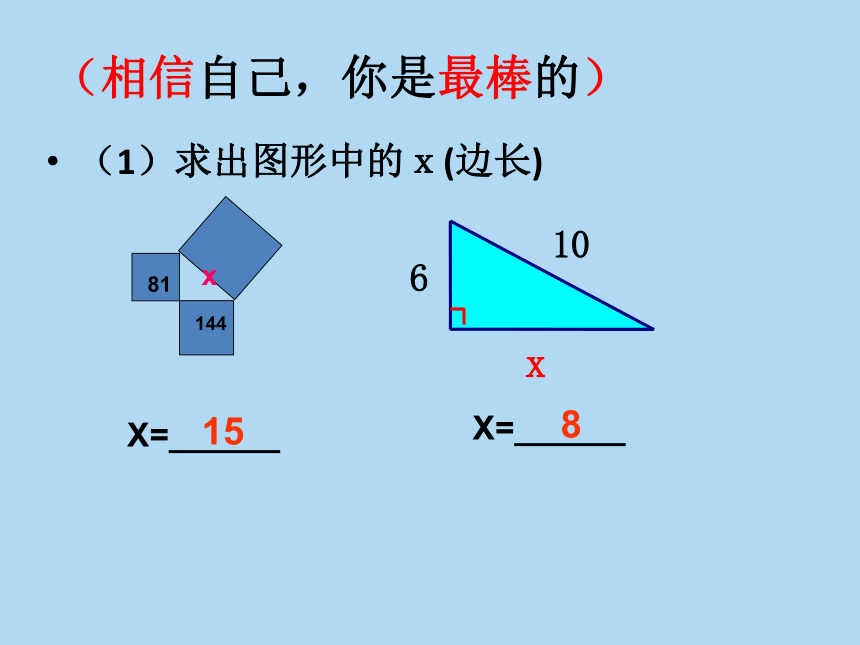
(1)求出图形中的x(边长)
81
144
x
X=______
X=______
15
8
(相信自己,你是最棒的)
6
x
10
3、若一个直角三角形两条直角边长是3和2,那么第三条边长是多少?
4、若一个直角三角形两条边长是3和2,那么第三条边长是多少?
w
。
5 矩形的一边长是5,对角线是13,则它的面积是 。
60
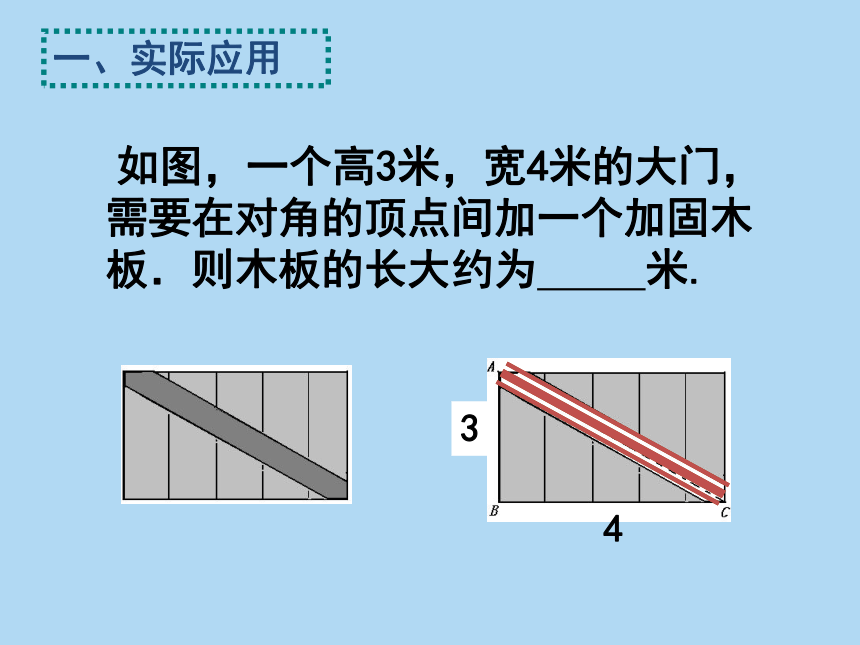
一、实际应用
如图,一个高3米,宽4米的大门,需要在对角的顶点间加一个加固木板.则木板的长大约为 米.
3
4
探究新知
一个门框的尺寸如图,一块长3m,宽2.2m的薄木板能否从门框内通过,为什么?
D
C
B
A
1m
2m
2.2m
实际问题
数学问题
2m
1m
A
B
C
巩固练习
1、如图,有一块长方形花圃,有少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了 m路,却踩伤了花草.
路
3m
4m
路
3m
4m
实际问题
数学问题
5
巩固练习
2、一旗杆离地面6米处折断,旗杆顶部落在离旗杆底部8米处,则旗杆折断前有 米。
A
B
C
6
8
50
例题解析
例1、有两棵松树,相距40米,已知它们的高度分别是36米,6米,则这两棵松树树顶之间的距离为 米.
A
C
E
B
D
36
6
30
40
巩固练习
3、如图,有一只小鸟从小树顶飞到大树顶上,试问它飞行的最短路程是多少米?(先画出示意图,然后再求解)
13m
8m
12m
实际问题
数学问题
例2 小明拿着一根长竹竿进一个宽为3m的城门,他把竹竿竖起来,发现竹竿比城门高1m,当他把竹竿斜着时,竹竿的两端刚好顶着城门的对角,问竹竿长多少米?
二、实际应用
D
C
B
A
3m
1m
x
x
(x+1)
(x+1)
x
3m
A
B
C
挑战自我
4、在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一
边,花朵齐及水面,已知红莲移动的
水平距离为2米,问这里的水有多深?
巩固练习
5、一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。
R
P
Q
20
6.已知一直角三角形的三边长都是正整
数,其中斜边长13,并且周长为30,
求其面积。
60
如图,小颖同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AB=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
三 (动手操作,合作探究)
解:在Rt△ABC中,勾股定理得AC=8
设CE为xcm
由折叠可知,BE=AE=(8-x)cm
在Rt△BCE中,由勾股定理得
BC2+CE2=BE2
即62+x2=(8-x)2
解之得x=7/4
勾股定理在折叠问题中的应用
例4.已知Rt△ABC中, ∠C=90°
若AC=5,AB=13,则△ABC的
周长 = ____.
面积 = ____.
AB边上的高CD=______
30
30
四、如何去求直角三角形斜边上的高
A
B
C
D
(6)如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
五、(在立体图形中的应用)
学生活动
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是4尺、3尺、12尺,那么,你能帮小明估计一下买的竹竿至多是多少尺吗?(结果取整数)
提示:长方体的高垂直于底面的任何一条直线
4
3
12
12
A
B
C
A
B
C
D
B
4
3
D
C
本节课小结:
1、本节课学习了哪些知识?
2、你积累了哪些方法?
3、谈谈你还存在哪些困惑?
……
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
55cm
10cm
6cm
55cm
48cm
感谢各位老师 光临指导!
这就是本届大会会徽的图案.
“赵爽弦图”表现了我国古人对数学的钻研精神和聪明才智。它是我国古代数学的骄傲.因此,这个图案被选为2002年在北京召开的国际数学家大会的会徽。
把勾股定理送到外星
球,与外星人进行数学交流 !
——华罗庚
勾股定理:
如果直角三角形的两直角边长分别为
a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则
a2+b2=c2
A
B
C
a
c
b
以直角三角形两条直角边为边长的正方形面积的和等于以斜边为边长的正方形的面积
(1)求出图形中的x(边长)
81
144
x
X=______
X=______
15
8
(相信自己,你是最棒的)
6
x
10
3、若一个直角三角形两条直角边长是3和2,那么第三条边长是多少?
4、若一个直角三角形两条边长是3和2,那么第三条边长是多少?
w
。
5 矩形的一边长是5,对角线是13,则它的面积是 。
60
一、实际应用
如图,一个高3米,宽4米的大门,需要在对角的顶点间加一个加固木板.则木板的长大约为 米.
3
4
探究新知
一个门框的尺寸如图,一块长3m,宽2.2m的薄木板能否从门框内通过,为什么?
D
C
B
A
1m
2m
2.2m
实际问题
数学问题
2m
1m
A
B
C
巩固练习
1、如图,有一块长方形花圃,有少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了 m路,却踩伤了花草.
路
3m
4m
路
3m
4m
实际问题
数学问题
5
巩固练习
2、一旗杆离地面6米处折断,旗杆顶部落在离旗杆底部8米处,则旗杆折断前有 米。
A
B
C
6
8
50
例题解析
例1、有两棵松树,相距40米,已知它们的高度分别是36米,6米,则这两棵松树树顶之间的距离为 米.
A
C
E
B
D
36
6
30
40
巩固练习
3、如图,有一只小鸟从小树顶飞到大树顶上,试问它飞行的最短路程是多少米?(先画出示意图,然后再求解)
13m
8m
12m
实际问题
数学问题
例2 小明拿着一根长竹竿进一个宽为3m的城门,他把竹竿竖起来,发现竹竿比城门高1m,当他把竹竿斜着时,竹竿的两端刚好顶着城门的对角,问竹竿长多少米?
二、实际应用
D
C
B
A
3m
1m
x
x
(x+1)
(x+1)
x
3m
A
B
C
挑战自我
4、在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一
边,花朵齐及水面,已知红莲移动的
水平距离为2米,问这里的水有多深?
巩固练习
5、一根32厘米的绳子被折成如图所示的形状钉在P、Q两点,PQ=16厘米,且RP⊥PQ,则RQ= 厘米。
R
P
Q
20
6.已知一直角三角形的三边长都是正整
数,其中斜边长13,并且周长为30,
求其面积。
60
如图,小颖同学折叠一个直角三角形的纸片,使A与B重合,折痕为DE,若已知AB=10cm,BC=6cm,你能求出CE的长吗?
C
A
B
D
E
三 (动手操作,合作探究)
解:在Rt△ABC中,勾股定理得AC=8
设CE为xcm
由折叠可知,BE=AE=(8-x)cm
在Rt△BCE中,由勾股定理得
BC2+CE2=BE2
即62+x2=(8-x)2
解之得x=7/4
勾股定理在折叠问题中的应用
例4.已知Rt△ABC中, ∠C=90°
若AC=5,AB=13,则△ABC的
周长 = ____.
面积 = ____.
AB边上的高CD=______
30
30
四、如何去求直角三角形斜边上的高
A
B
C
D
(6)如图,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程( 取3)是( )
A.20cm B.10cm C.14cm D.无法确定
B
B
8
O
A
2
蛋糕
A
C
B
8
周长的一半
6
五、(在立体图形中的应用)
学生活动
小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最长的吧!
快点回家,好用它凉衣服。
糟糕,太长了,放不进去。
如果电梯的长、宽、高分别是4尺、3尺、12尺,那么,你能帮小明估计一下买的竹竿至多是多少尺吗?(结果取整数)
提示:长方体的高垂直于底面的任何一条直线
4
3
12
12
A
B
C
A
B
C
D
B
4
3
D
C
本节课小结:
1、本节课学习了哪些知识?
2、你积累了哪些方法?
3、谈谈你还存在哪些困惑?
……
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?
B
A
A
B
C
55cm
10cm
6cm
55cm
48cm
感谢各位老师 光临指导!
