2021-2022学年人教版八年级数学下册17.1勾股定理 课件(33张ppt)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1勾股定理 课件(33张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 958.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 20:24:39 | ||
图片预览


文档简介
(共33张PPT)
第一课时:17.1勾股定理(1)
毕达哥拉斯,古希腊数学家哲学家,有一天,他应邀到朋友家做客,发现朋友家地砖的形状具有某种性质
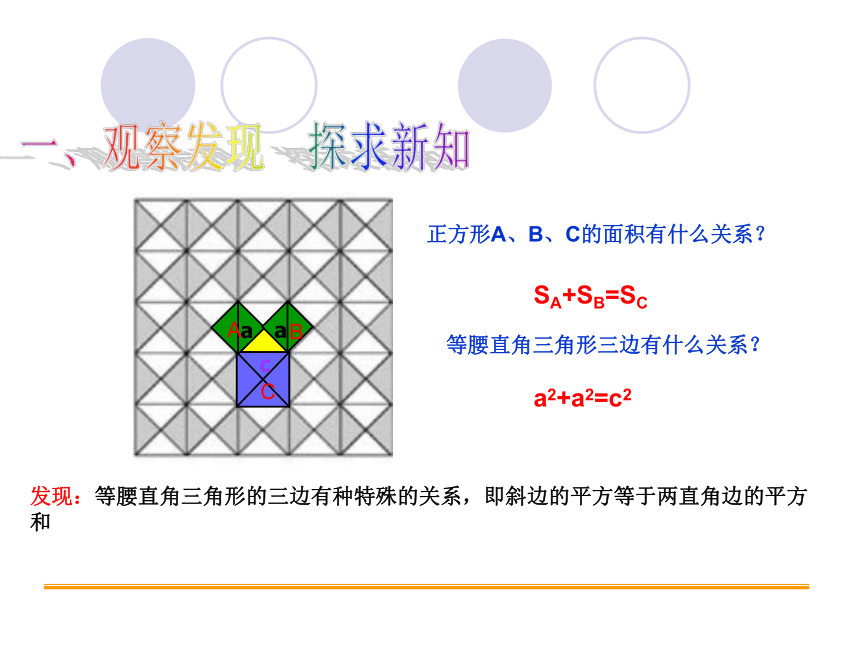
一、观察发现 探求新知
正方形A、B、C的面积有什么关系?
等腰直角三角形三边有什么关系?
SA+SB=SC
发现:等腰直角三角形的三边有种特殊的关系,即斜边的平方等于两直角边的平方和
a
a
c
a2+a2=c2
A
B
C
图18.1-2
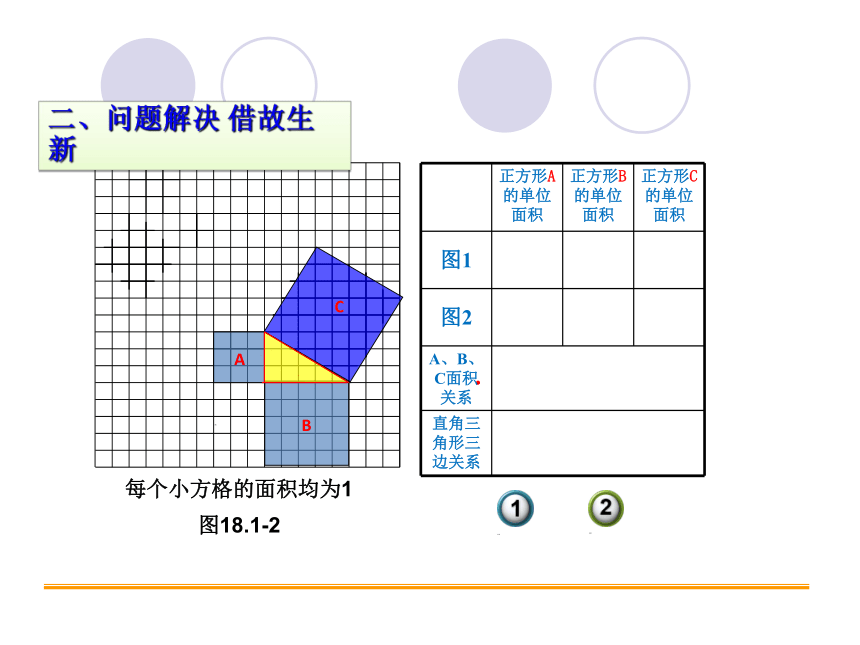
每个小方格的面积均为1
A
B
C
图1
正方形A的单位面积 正方形B的单位面积 正方形C的单位面积
图1
图2
A、B、C面积关系
直角三角形三边关系
1
2
分割
补全
二、问题解决 借故生新
a
b
c
正方形A的单位面积 正方形B的单位面积 正方形C的单位面积
图1
图2
A、B、C面积关系
直角三角形三边关系
图18.1-2
每个小方格的面积均为1
A
B
C
图1
1
2
分割
补全
A
B
C
图2
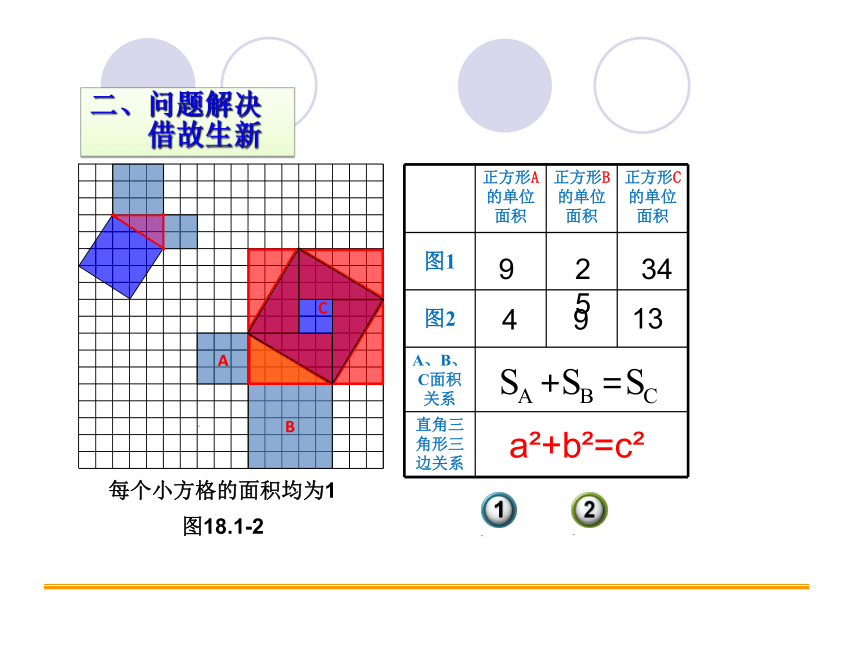
4
9
13
a +b =c
9
25
34
二、问题解决
借故生新
a
b
c
a
b
c
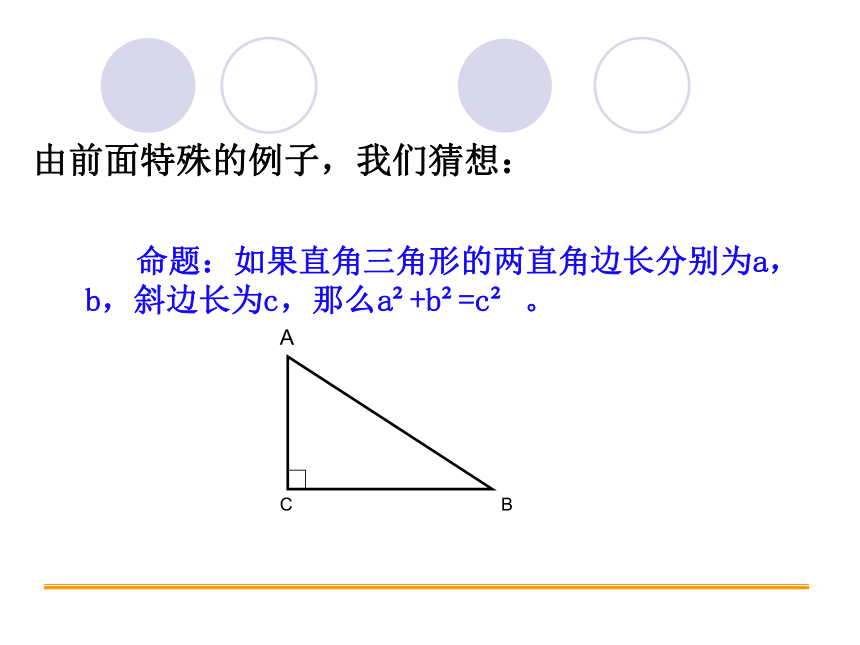
命题:如果直角三角形的两直角边长分别为a,
b,斜边长为c,那么a +b =c 。
由前面特殊的例子,我们猜想:
A
C
B
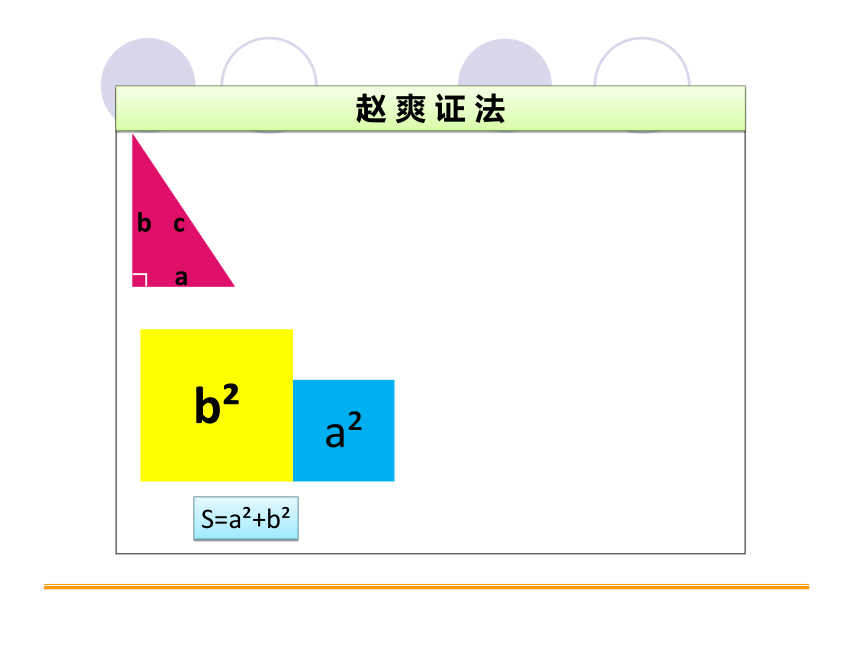
S=a +b
b
a
b
a
c
赵 爽 证 法
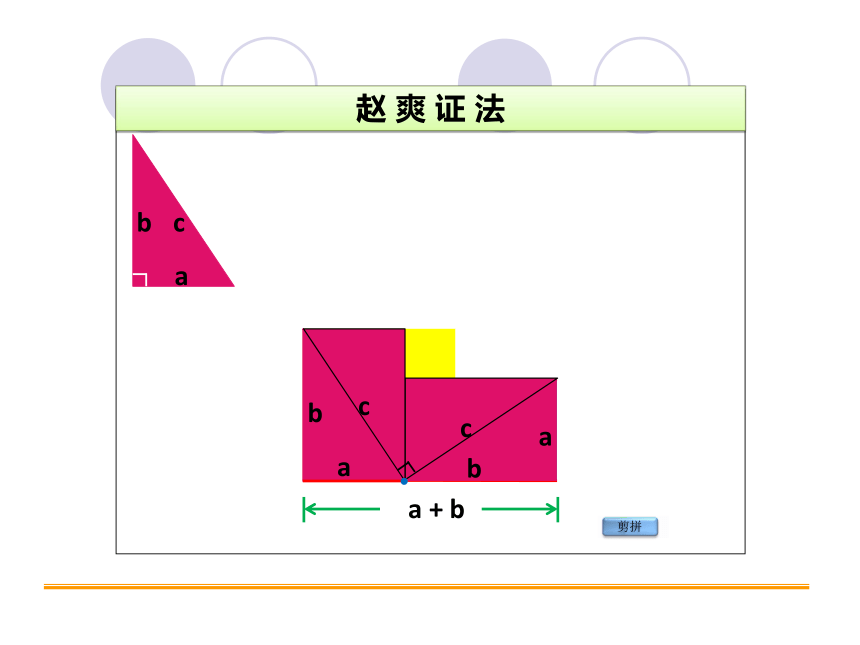
a + b
c
a
b
c
b
a
b
a
c
赵 爽 证 法
剪拼
a
b
b
a
c
c
c
c
b
a
c
剪拼
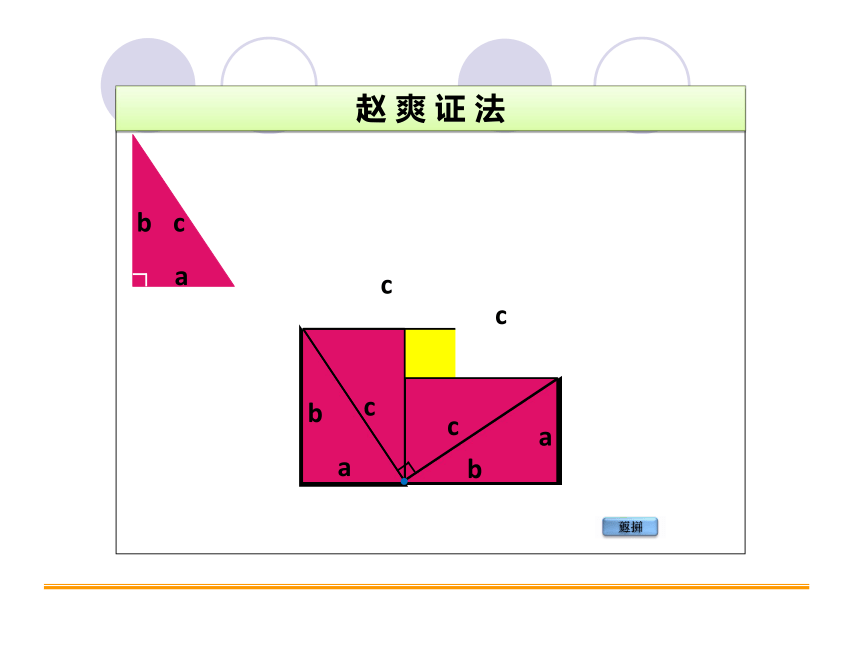
返回
赵 爽 证 法
b
a
c
c
c
c
c
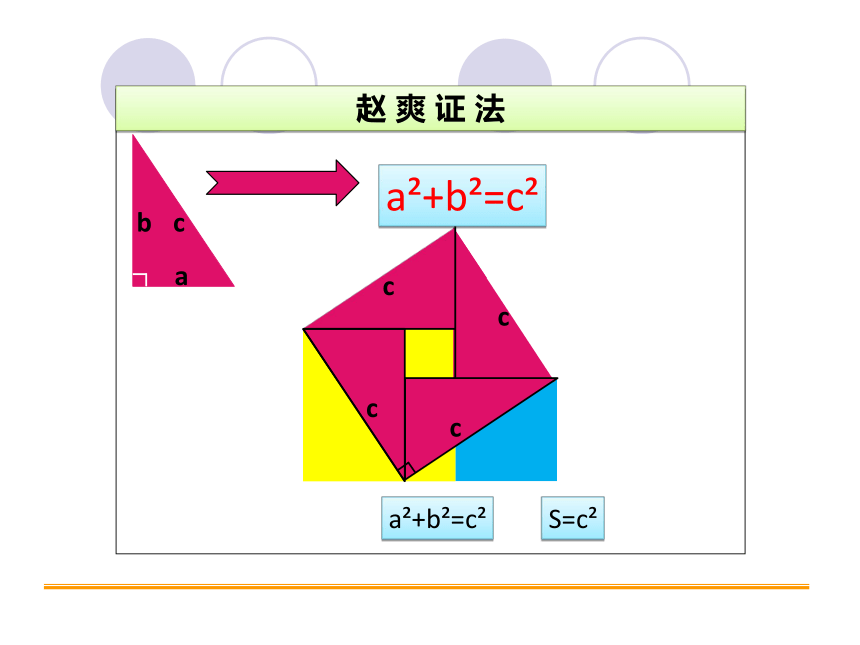
S=a +b
b
a
S=c
a +b =c
赵 爽 证 法
a +b =c
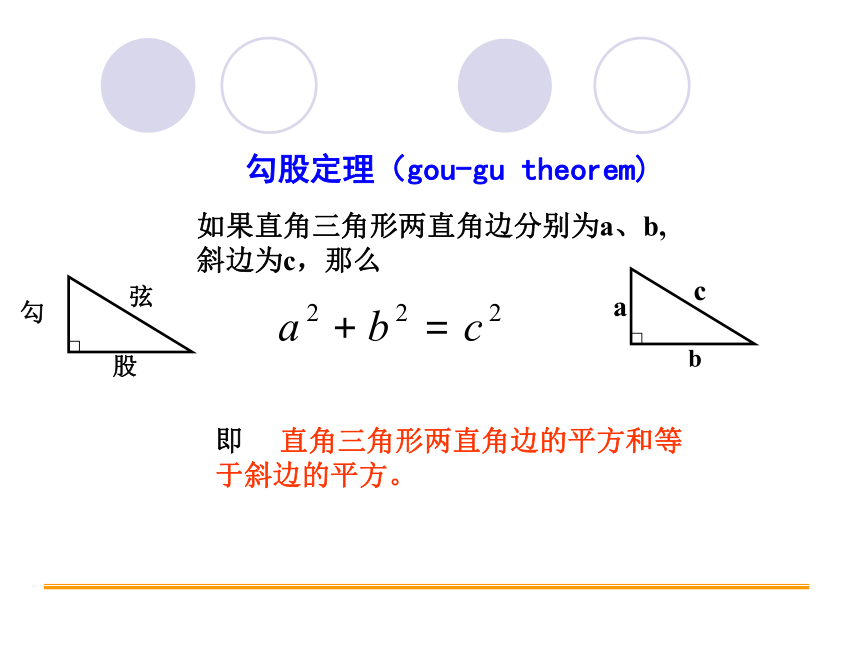
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
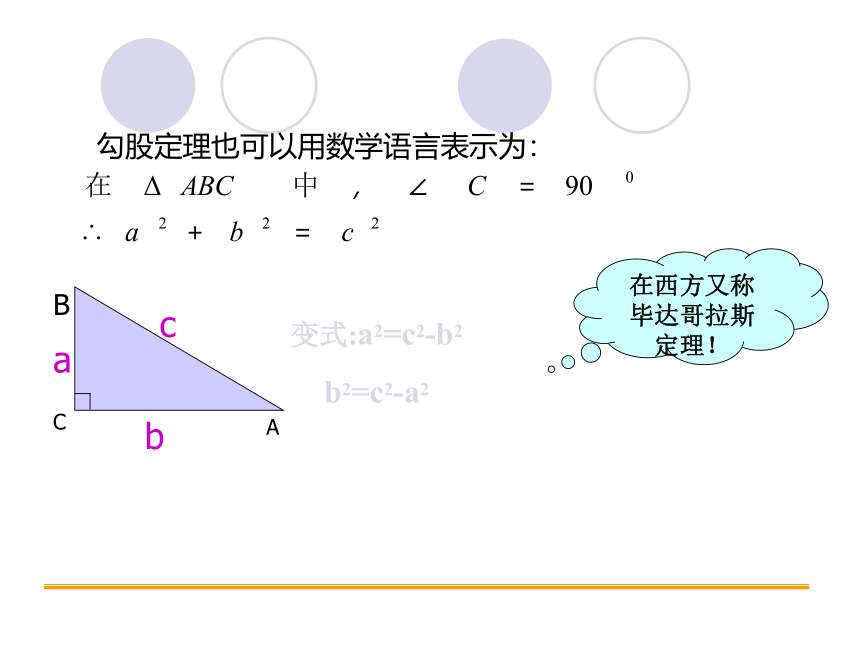
勾股定理也可以用数学语言表示为:
a
c
b
A
C
B
在西方又称毕达哥拉斯定理!
变式:a2=c2-b2
b2=c2-a2
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
2m
D
C
A
B
解:连结AC,在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5
因此,AC= ≈2.236
因为AC大于木板的宽,
所以木板能 从门框内通过.
1m
问题1
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的面积分别是3 ,4,1,3,求最大正方形E的面积.
勾股树
F
G
s正方形A
+
s正方形B
=
s正方形F
s正方形C
+
s正方形D
=
s正方形G
s正方形F
+
s正方形G
=
s正方形E
问题2
=4
=7
=11
小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
问题3
勾股定理:
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即a2 + b2 = c2
公式变形:
a2 = c2 - b2 c=
b2 = c2 - a2 a=
b=
课堂小结
勾股定理的主要用途是 : 在直角三角形中,
1、已知任意两边求第三边的长;
2、已知一边及另两边的关系,求另两边.
c
a
b
B
A
C
勾
弦
股
第二课时
说出下列数轴上各字母所表示的实数
A B C D
-2 -1 0 1 2
实数
数轴上的点
一一对应
上面数轴上的点表示的都是_____数
你能在数轴上能表示无理数吗?
有理
创设情境 引入新课
自主学习 预习检测
你能画出斜边为 的三角形吗?斜边为 呢?
1.已知直角三角形ABC的三边为a、b、c , ∠C= 90°,则 a、b、c 三者之间的关系是 ;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是 ;Zx```x`````k
3. 叫做无理数.
合作探究 精讲点拨
-1 0 1 2 3
你能在数轴上表示出 的点吗?
√
√
你能在数轴上画出表示 的点吗?
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
你能在数轴上画出表示 的点吗?
如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为 的线段
A
利用勾股定理证明HL
问题1:在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能用一般三角形全等的判定方法证明这一结论吗?
追问1:命题的证明一般分为哪几个步骤?
追问2:要证明这两个直角三角形三角形全等,我们有什么已知条件?还缺什么条件就可以证明?
追问3:能通过现有的条件证明BC=B'C'吗?用什么方法?
根据图,写出已知、求证如下:
A
B
C
A'
B'
C'
图1
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90 ,AB=A'B',AC=A'C'.
求证:△ABC≌△A'B'C'.
证明:∵在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90 ,
根据勾股定理得,.
又∵AB=A'B',AC=A'C',
∴BC=B'C'.
∴△ABC≌△A'B'C'(SSS).
A
B
C
A'
B'
C'
图1
如图,在△ABC中,∠ACB=900,,,AC=2,BC=
1求△ABC的高,
2△ABC的面积。
C
A
B
等面积法
在△ABC中,AB=15,BC=14,AC=13,
求△ABC的面积;
A
B
C
D
x
14-x
E
方程思想
等面积法
你会求腰AC上的高吗?
如图,在△ABC中,∠ACB=900,CD⊥AB,垂足为D,若∠B=300,AD=1求高CD和△ABC的面积。
C
A
B
D
双垂图
练习2:如图,等边三角形的边长是6.
求:(1)高AD的长;
(2)这个三角形的面积.
如图所示,要修一个种植蔬菜的育苗大棚,棚宽a=2m,高b=1.5m,长d=12m,则修盖在顶上的塑料薄膜需要的面积为多少
a
b
c
d
第4题图
A
D
C
B
1.已知等腰三角形的一条腰长是5,底边长是6,则它底边上的高为 .
2 .长为 的线段是直角边长为正整数 , 的直角三角形的斜边.
3 .如图所示,在正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边数为( )
A.0 B.1 C.2 D.3
4.如图所示,等边三角形ABC的边长为8.(1)求高AD的长;
(2)求这个三角形的面积(答案可保留根号).
C
1
5
4
第3题图
A
C
B
典型训练 夯实基础
如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
x
x
总结提升 当堂检测
第一课时:17.1勾股定理(1)
毕达哥拉斯,古希腊数学家哲学家,有一天,他应邀到朋友家做客,发现朋友家地砖的形状具有某种性质
一、观察发现 探求新知
正方形A、B、C的面积有什么关系?
等腰直角三角形三边有什么关系?
SA+SB=SC
发现:等腰直角三角形的三边有种特殊的关系,即斜边的平方等于两直角边的平方和
a
a
c
a2+a2=c2
A
B
C
图18.1-2
每个小方格的面积均为1
A
B
C
图1
正方形A的单位面积 正方形B的单位面积 正方形C的单位面积
图1
图2
A、B、C面积关系
直角三角形三边关系
1
2
分割
补全
二、问题解决 借故生新
a
b
c
正方形A的单位面积 正方形B的单位面积 正方形C的单位面积
图1
图2
A、B、C面积关系
直角三角形三边关系
图18.1-2
每个小方格的面积均为1
A
B
C
图1
1
2
分割
补全
A
B
C
图2
4
9
13
a +b =c
9
25
34
二、问题解决
借故生新
a
b
c
a
b
c
命题:如果直角三角形的两直角边长分别为a,
b,斜边长为c,那么a +b =c 。
由前面特殊的例子,我们猜想:
A
C
B
S=a +b
b
a
b
a
c
赵 爽 证 法
a + b
c
a
b
c
b
a
b
a
c
赵 爽 证 法
剪拼
a
b
b
a
c
c
c
c
b
a
c
剪拼
返回
赵 爽 证 法
b
a
c
c
c
c
c
S=a +b
b
a
S=c
a +b =c
赵 爽 证 法
a +b =c
勾股定理(gou-gu theorem)
如果直角三角形两直角边分别为a、b,斜边为c,那么
即 直角三角形两直角边的平方和等于斜边的平方。
a
b
c
勾
股
弦
勾股定理也可以用数学语言表示为:
a
c
b
A
C
B
在西方又称毕达哥拉斯定理!
变式:a2=c2-b2
b2=c2-a2
一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过 为什么
2m
D
C
A
B
解:连结AC,在Rt△ABC中,根据勾股定理,
AC2=AB2+BC2=12+22=5
因此,AC= ≈2.236
因为AC大于木板的宽,
所以木板能 从门框内通过.
1m
问题1
如图,图中所有的三角形都是直角三角形,四边形都是正方形.已知正方形A,B,C,D的面积分别是3 ,4,1,3,求最大正方形E的面积.
勾股树
F
G
s正方形A
+
s正方形B
=
s正方形F
s正方形C
+
s正方形D
=
s正方形G
s正方形F
+
s正方形G
=
s正方形E
问题2
=4
=7
=11
小强想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,你能帮他算出来吗?
A
B
C
5米
(X+1)米
x米
问题3
勾股定理:
直角三角形两直角边a ,b的平方和,等于斜边为c的平方. 即a2 + b2 = c2
公式变形:
a2 = c2 - b2 c=
b2 = c2 - a2 a=
b=
课堂小结
勾股定理的主要用途是 : 在直角三角形中,
1、已知任意两边求第三边的长;
2、已知一边及另两边的关系,求另两边.
c
a
b
B
A
C
勾
弦
股
第二课时
说出下列数轴上各字母所表示的实数
A B C D
-2 -1 0 1 2
实数
数轴上的点
一一对应
上面数轴上的点表示的都是_____数
你能在数轴上能表示无理数吗?
有理
创设情境 引入新课
自主学习 预习检测
你能画出斜边为 的三角形吗?斜边为 呢?
1.已知直角三角形ABC的三边为a、b、c , ∠C= 90°,则 a、b、c 三者之间的关系是 ;
2.若一个直角三角形两条直角边长是3和2,那么第三条边长是 ;Zx```x`````k
3. 叫做无理数.
合作探究 精讲点拨
-1 0 1 2 3
你能在数轴上表示出 的点吗?
√
√
你能在数轴上画出表示 的点吗?
0
1
2
3
4
步骤:
l
A
B
C
1、在数轴上找到点A,使OA=3;
2、作直线l⊥OA,在l上取一点B,使AB=2;
3,以原点O为圆心,以OB为半径作弧,弧与数轴交于C点,则点C即为表示 的点。
你能在数轴上画出表示 的点和 的点吗?
∴点C即为表示 的点
你能在数轴上画出表示 的点吗?
如图为4×4的正方形网格,以格点与点A为端点,你能画出几条边长为 的线段
A
利用勾股定理证明HL
问题1:在八年级上册中我们曾经通过画图得到结论:斜边和一条直角边对应相等的两个直角三角形全等.学习了勾股定理后,你能用一般三角形全等的判定方法证明这一结论吗?
追问1:命题的证明一般分为哪几个步骤?
追问2:要证明这两个直角三角形三角形全等,我们有什么已知条件?还缺什么条件就可以证明?
追问3:能通过现有的条件证明BC=B'C'吗?用什么方法?
根据图,写出已知、求证如下:
A
B
C
A'
B'
C'
图1
已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90 ,AB=A'B',AC=A'C'.
求证:△ABC≌△A'B'C'.
证明:∵在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90 ,
根据勾股定理得,.
又∵AB=A'B',AC=A'C',
∴BC=B'C'.
∴△ABC≌△A'B'C'(SSS).
A
B
C
A'
B'
C'
图1
如图,在△ABC中,∠ACB=900,,,AC=2,BC=
1求△ABC的高,
2△ABC的面积。
C
A
B
等面积法
在△ABC中,AB=15,BC=14,AC=13,
求△ABC的面积;
A
B
C
D
x
14-x
E
方程思想
等面积法
你会求腰AC上的高吗?
如图,在△ABC中,∠ACB=900,CD⊥AB,垂足为D,若∠B=300,AD=1求高CD和△ABC的面积。
C
A
B
D
双垂图
练习2:如图,等边三角形的边长是6.
求:(1)高AD的长;
(2)这个三角形的面积.
如图所示,要修一个种植蔬菜的育苗大棚,棚宽a=2m,高b=1.5m,长d=12m,则修盖在顶上的塑料薄膜需要的面积为多少
a
b
c
d
第4题图
A
D
C
B
1.已知等腰三角形的一条腰长是5,底边长是6,则它底边上的高为 .
2 .长为 的线段是直角边长为正整数 , 的直角三角形的斜边.
3 .如图所示,在正方形网格中,每个小正方形的边长为1,则在网格上的三角形ABC中,边长为无理数的边数为( )
A.0 B.1 C.2 D.3
4.如图所示,等边三角形ABC的边长为8.(1)求高AD的长;
(2)求这个三角形的面积(答案可保留根号).
C
1
5
4
第3题图
A
C
B
典型训练 夯实基础
如图,∠ACB=∠ABD=90°,CA=CB,∠DAB=30°,AD=8,求AC的长。
解:
∵∠ABD=90°,∠DAB=30°
∴BD= AD=4
在Rt△ABD中
,根据勾股定理
在Rt△ABC中,
又AD=8
A
B
C
D
30°
x
x
总结提升 当堂检测
