人教版2021-2022学年八年级数学下册17.1勾股定理 (30张ppt)
文档属性
| 名称 | 人教版2021-2022学年八年级数学下册17.1勾股定理 (30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 20:20:01 | ||
图片预览




文档简介
(共30张PPT)
17.1 勾股定理(1)
人教版 八年级数学(下册)
——数形结合之美
学习目标
1.经历勾股定理的探究过程,了解关于勾股定理
的一些文化历史背景,并能证明勾股定理;
2.能用勾股定理解决一些简单问题.
国际数学家大会是最高水平的全球性数学科学学术
会议.2002年在北京召开了第24届国际数学家大会.如
图就是大会的会徽的图案.
创设情境 引入课题
问题1 你见过这个图案吗?
它由哪些基本图形组成?
追问 等腰直角三角形三条边之间有什么关系?
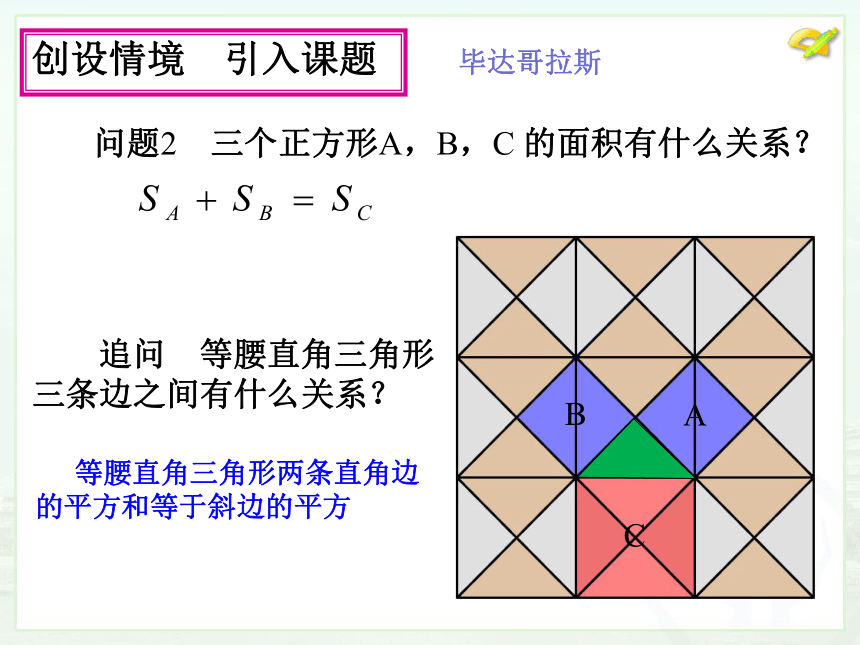
创设情境 引入课题
问题2 三个正方形A,B,C 的面积有什么关系?
A
B
C
等腰直角三角形两条直角边的平方和等于斜边的平方
毕达哥拉斯
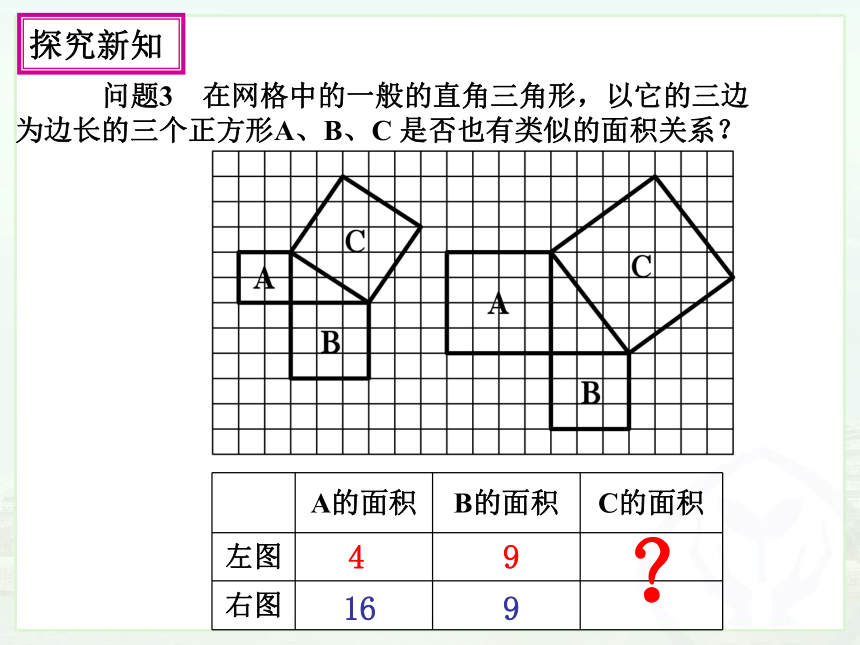
问题3 在网格中的一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?
A的面积 B的面积 C的面积
左图
右图
4
?
9
16
9
探究新知
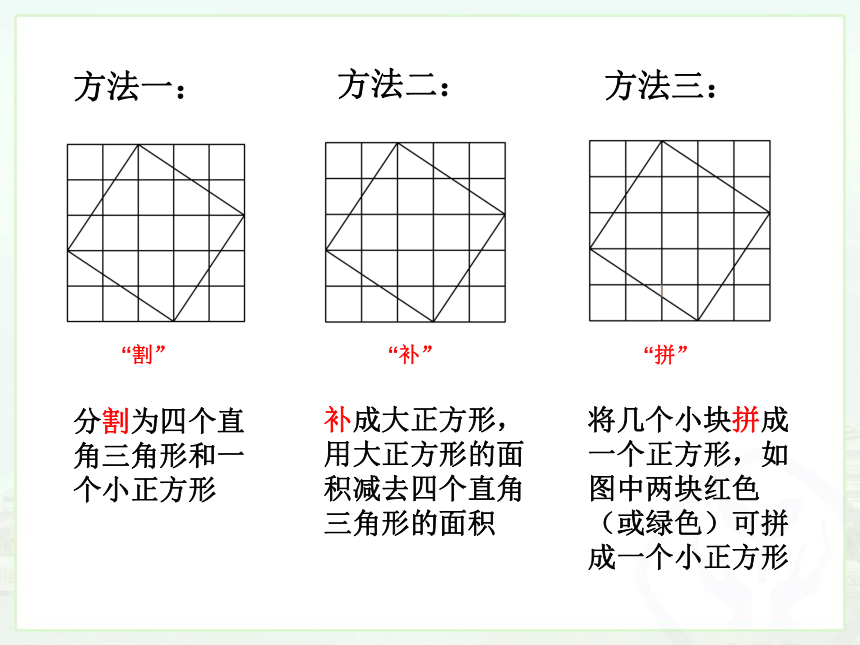
“割”
“补”
“拼”
方法一:
方法二:
方法三:
分割为四个直角三角形和一个小正方形
补成大正方形,用大正方形的面积减去四个直角三角形的面积
将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形
A的面积 B的面积 C的面积
左图
右图
4
?
9
16
9
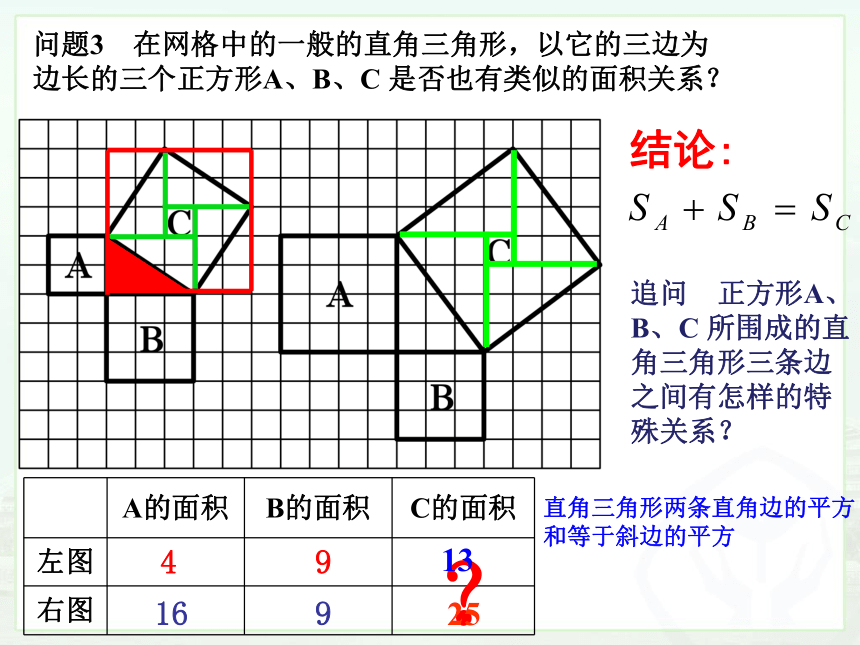
结论:
25
13
追问 正方形A、B、C 所围成的直角三角形三条边
之间有怎样的特殊关系?
问题3 在网格中的一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?
直角三角形两条直角边的平方和等于斜边的平方
猜想:
如果直角三角形两直角边长分别为a,b,
斜边长为c,
猜想
问题4 通过前面的探究活动,直角三角形
三边之间有什么关系?
那么a2+b2=c2.
追问 以上直角三角形的边长都是具体的数值,
任意边长直角三角形三边有这样的关系吗?
c
a
b
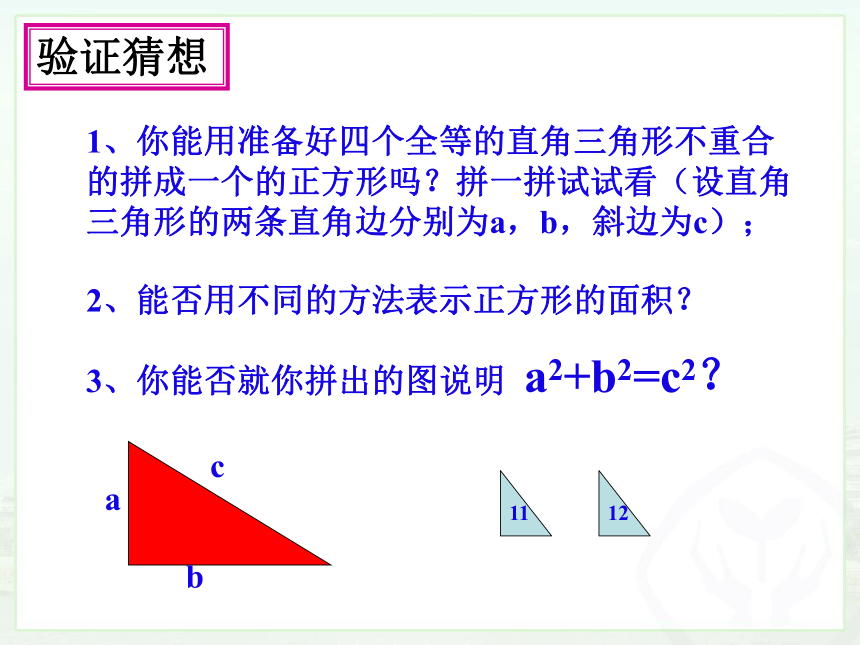
1、你能用准备好四个全等的直角三角形不重合的拼成一个的正方形吗?拼一拼试试看(设直角三角形的两条直角边分别为a,b,斜边为c);
2、能否用不同的方法表示正方形的面积?
3、你能否就你拼出的图说明 a2+b2=c2?
验证猜想
11
12
c
a
b
c
a
b
c
a
b
c
a
b
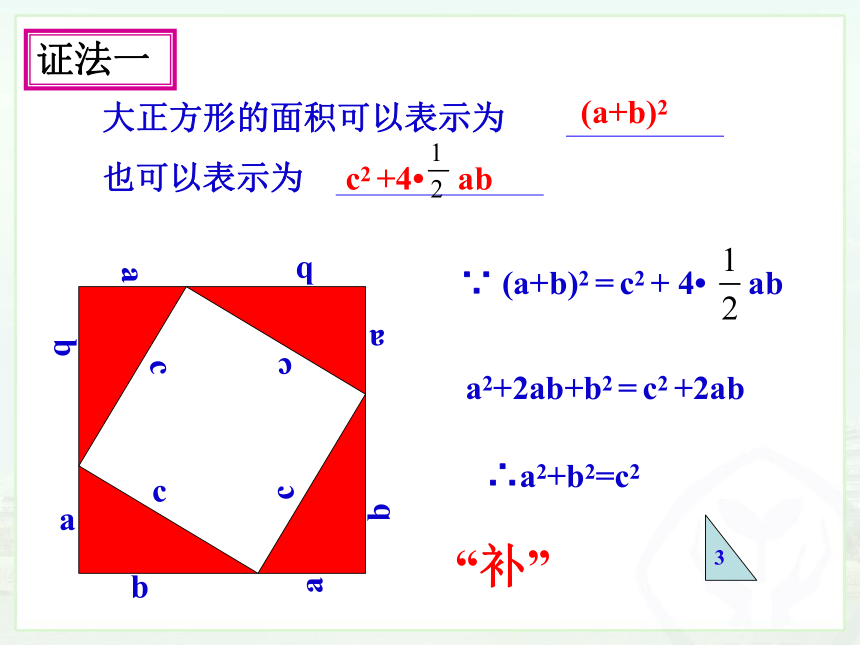
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为
也可以表示为
(a+b)2
c2 +4 ab
证法一
“补”
3
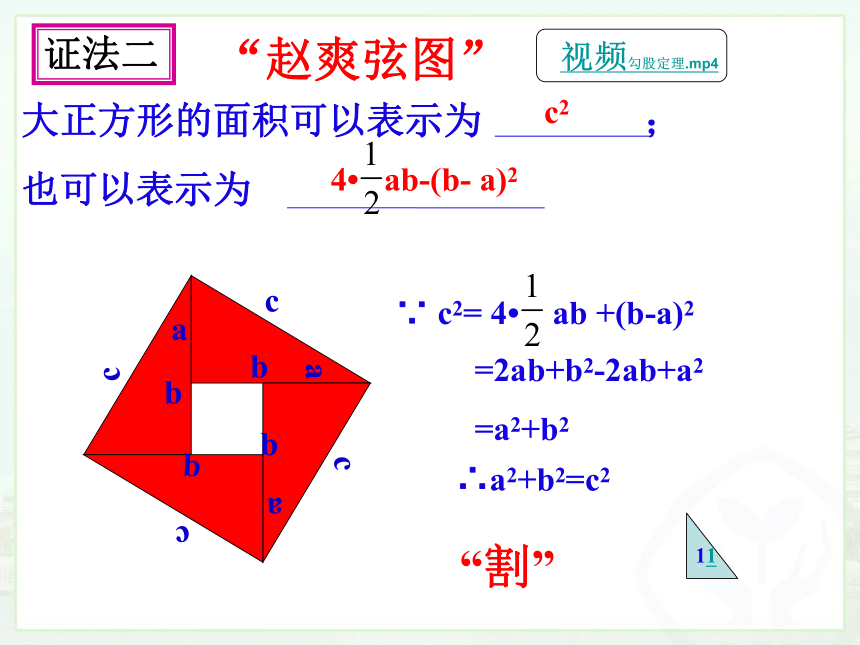
大正方形的面积可以表示为 ;
也可以表示为
4 ab-(b- a)2
c
a
b
c
a
b
c
a
b
c
a
b
=a2+b2
∴a2+b2=c2
c2
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
“赵爽弦图”
证法二
“割”
视频勾股定理.mp4
11
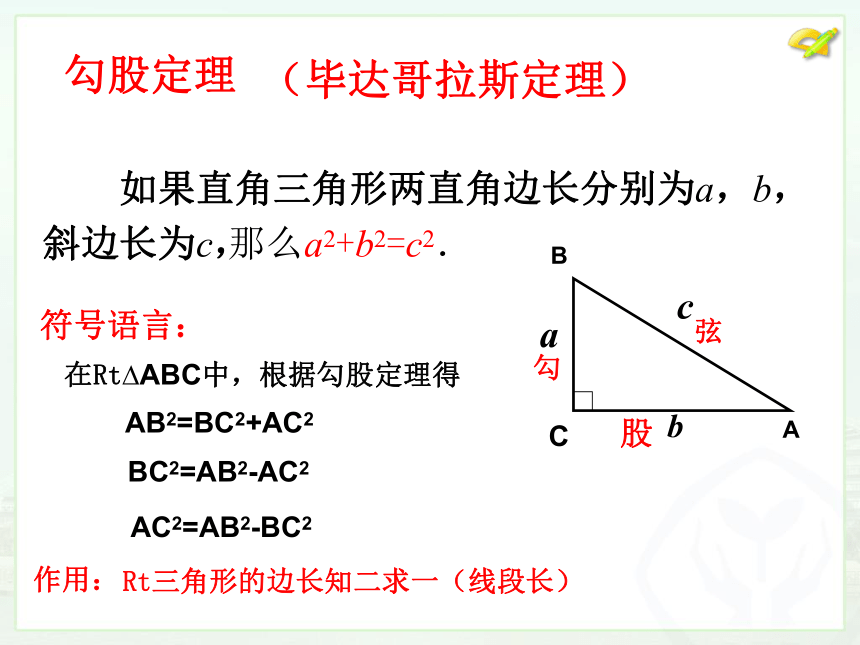
如果直角三角形两直角边长分别为a,b,
斜边长为c,
勾股定理
那么a2+b2=c2.
(毕达哥拉斯定理)
a
b
c
符号语言:
A
B
C
AB2=BC2+AC2
BC2=AB2-AC2
AC2=AB2-BC2
在Rt ABC中,根据勾股定理得
作用:
Rt三角形的边长知二求一(线段长)
勾
股
弦
a
a
b
b
c
c
“总统证法”.
美国第二十任总统伽菲尔德的证法
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
证法三
杜梁伟证法
证法四
杜梁伟证法
证法五
“毕达哥拉斯证法”
∴a2+b2=c2
左图面积可以表示为:
右图面积可以表示为:
证法六
青朱出入图:以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
约公元 263 年,三国时代魏国的数学家刘徽为古籍《九章算术》作注释时,用“出入相补法”证明了勾股定理。
证法七
a
b
c
无字证明
①
②
③
④
⑤
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
a
b
c
A
B
C
D
E
F
O
意大利文艺复兴时代的著名画家达·芬奇对勾股定理进行了研究。
达·芬奇证法
证法八
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
在Rt△ABC中,AB=5,AC=3,求BC的长?
例1:
5
13
A
B
C
解:
在Rt△ABC中,根据勾股定理得
BC2=AB2-AC2
=132-52
=144
5 12 13
在Rt△ABC中,AC=3,AB+BC=9,求AB、BC的长?
例2:
9-x
3
x
A
B
C
解:
在Rt△ABC中,根据勾股定理得
AB2=BC2+AC2
∴x2=(9-x)2+32
3 4 5
设AB=x,则BC=9-x
∴x2=81-18x+x2+9
∴18x=90
∴x=5
则AB=5,BC=9-x=4
在Rt△ABC中,AC=1,∠B=30°,求AB、BC的长?
例3:
1
A
B
C
解:
根据勾股定理得
Rt△ABC中,∠B=30°
1 2
∴AB=2AC=2
2
1.求出下列直角三角形中未知边的长度:
8
15
A
B
C
解:
(1)在Rt△ABC中,根据勾股定理得
8 15 17
巩固练习
C
B
A
5
10
?
(2)在Rt△ABC中,根据勾股定理得
2. 如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别
是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
巩固练习
通过这种方法,可以把一个正方形的面积分成若干
个小正方形的面积的和,不断地分下去,就可以得到一
棵美丽的勾股树.
巩固练习
在Rt△ABC中,∠A=30°,AC=2,求AB、BC的长?
能力提升
2
B
C
A
解:
根据勾股定理得
在Rt△ABC中,∠A=30°
∴AB=2BC=2x
设 BC=x
AB2-BC2=AC2
∴(2x)2--x2=22
∴3x2=4
∴x2=
∴x=
则AB= ,BC=
x
2x
在三角形ABC中,∠C=90°,AC=4,
BC=3, CD是AB边上的高,求CD的长度?
4
3
A
B
C
D
能力提升
如果直角三角形两直角边长分别为a,b,斜边长为c,
小结
知道两条直角边,求斜边用 法;
加
Rt△ABC
知道斜边和一直角边,求另一直角边用 法。
减
那么 a2+b2=c2
1、勾股定理的内容?
2.勾股定理有什么作用?
3.阅读教科书、回看课件,总结勾股定理的其他证明方法.了解中国人的伟大和外国人的智慧.
Rt三角形的边长知二求一(线段长)
17.1 勾股定理(1)
人教版 八年级数学(下册)
——数形结合之美
学习目标
1.经历勾股定理的探究过程,了解关于勾股定理
的一些文化历史背景,并能证明勾股定理;
2.能用勾股定理解决一些简单问题.
国际数学家大会是最高水平的全球性数学科学学术
会议.2002年在北京召开了第24届国际数学家大会.如
图就是大会的会徽的图案.
创设情境 引入课题
问题1 你见过这个图案吗?
它由哪些基本图形组成?
追问 等腰直角三角形三条边之间有什么关系?
创设情境 引入课题
问题2 三个正方形A,B,C 的面积有什么关系?
A
B
C
等腰直角三角形两条直角边的平方和等于斜边的平方
毕达哥拉斯
问题3 在网格中的一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?
A的面积 B的面积 C的面积
左图
右图
4
?
9
16
9
探究新知
“割”
“补”
“拼”
方法一:
方法二:
方法三:
分割为四个直角三角形和一个小正方形
补成大正方形,用大正方形的面积减去四个直角三角形的面积
将几个小块拼成一个正方形,如图中两块红色(或绿色)可拼成一个小正方形
A的面积 B的面积 C的面积
左图
右图
4
?
9
16
9
结论:
25
13
追问 正方形A、B、C 所围成的直角三角形三条边
之间有怎样的特殊关系?
问题3 在网格中的一般的直角三角形,以它的三边为边长的三个正方形A、B、C 是否也有类似的面积关系?
直角三角形两条直角边的平方和等于斜边的平方
猜想:
如果直角三角形两直角边长分别为a,b,
斜边长为c,
猜想
问题4 通过前面的探究活动,直角三角形
三边之间有什么关系?
那么a2+b2=c2.
追问 以上直角三角形的边长都是具体的数值,
任意边长直角三角形三边有这样的关系吗?
c
a
b
1、你能用准备好四个全等的直角三角形不重合的拼成一个的正方形吗?拼一拼试试看(设直角三角形的两条直角边分别为a,b,斜边为c);
2、能否用不同的方法表示正方形的面积?
3、你能否就你拼出的图说明 a2+b2=c2?
验证猜想
11
12
c
a
b
c
a
b
c
a
b
c
a
b
∵ (a+b)2 = c2 + 4 ab
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
大正方形的面积可以表示为
也可以表示为
(a+b)2
c2 +4 ab
证法一
“补”
3
大正方形的面积可以表示为 ;
也可以表示为
4 ab-(b- a)2
c
a
b
c
a
b
c
a
b
c
a
b
=a2+b2
∴a2+b2=c2
c2
∵ c2= 4 ab +(b-a)2
=2ab+b2-2ab+a2
“赵爽弦图”
证法二
“割”
视频勾股定理.mp4
11
如果直角三角形两直角边长分别为a,b,
斜边长为c,
勾股定理
那么a2+b2=c2.
(毕达哥拉斯定理)
a
b
c
符号语言:
A
B
C
AB2=BC2+AC2
BC2=AB2-AC2
AC2=AB2-BC2
在Rt ABC中,根据勾股定理得
作用:
Rt三角形的边长知二求一(线段长)
勾
股
弦
a
a
b
b
c
c
“总统证法”.
美国第二十任总统伽菲尔德的证法
如图,梯形由三个直角三角形组合而成,利用面积公式,列出代数关系式,得
化简,得
证法三
杜梁伟证法
证法四
杜梁伟证法
证法五
“毕达哥拉斯证法”
∴a2+b2=c2
左图面积可以表示为:
右图面积可以表示为:
证法六
青朱出入图:以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
约公元 263 年,三国时代魏国的数学家刘徽为古籍《九章算术》作注释时,用“出入相补法”证明了勾股定理。
证法七
a
b
c
无字证明
①
②
③
④
⑤
以刘徽的“青朱出入图”为代表,证明不需用任何数学符号和文字,更不需进行运算,隐含在图中的勾股定理便清晰地呈现,整个证明单靠移动几块图形而得出,被称为“无字证明”。
a
b
c
A
B
C
D
E
F
O
意大利文艺复兴时代的著名画家达·芬奇对勾股定理进行了研究。
达·芬奇证法
证法八
Ⅰ
Ⅱ
A
a
B
C
b
D
E
F
O
Ⅰ
Ⅱ
A′
B′
C′
D′
E′
F′
在Rt△ABC中,AB=5,AC=3,求BC的长?
例1:
5
13
A
B
C
解:
在Rt△ABC中,根据勾股定理得
BC2=AB2-AC2
=132-52
=144
5 12 13
在Rt△ABC中,AC=3,AB+BC=9,求AB、BC的长?
例2:
9-x
3
x
A
B
C
解:
在Rt△ABC中,根据勾股定理得
AB2=BC2+AC2
∴x2=(9-x)2+32
3 4 5
设AB=x,则BC=9-x
∴x2=81-18x+x2+9
∴18x=90
∴x=5
则AB=5,BC=9-x=4
在Rt△ABC中,AC=1,∠B=30°,求AB、BC的长?
例3:
1
A
B
C
解:
根据勾股定理得
Rt△ABC中,∠B=30°
1 2
∴AB=2AC=2
2
1.求出下列直角三角形中未知边的长度:
8
15
A
B
C
解:
(1)在Rt△ABC中,根据勾股定理得
8 15 17
巩固练习
C
B
A
5
10
?
(2)在Rt△ABC中,根据勾股定理得
2. 如图,所有的三角形都是直角三角形,四
边形都是正方形,已知正方形A,B,C,D 的边长分别
是12,16,9,12.求最大正方形E 的面积.
A
B
C
D
E
巩固练习
通过这种方法,可以把一个正方形的面积分成若干
个小正方形的面积的和,不断地分下去,就可以得到一
棵美丽的勾股树.
巩固练习
在Rt△ABC中,∠A=30°,AC=2,求AB、BC的长?
能力提升
2
B
C
A
解:
根据勾股定理得
在Rt△ABC中,∠A=30°
∴AB=2BC=2x
设 BC=x
AB2-BC2=AC2
∴(2x)2--x2=22
∴3x2=4
∴x2=
∴x=
则AB= ,BC=
x
2x
在三角形ABC中,∠C=90°,AC=4,
BC=3, CD是AB边上的高,求CD的长度?
4
3
A
B
C
D
能力提升
如果直角三角形两直角边长分别为a,b,斜边长为c,
小结
知道两条直角边,求斜边用 法;
加
Rt△ABC
知道斜边和一直角边,求另一直角边用 法。
减
那么 a2+b2=c2
1、勾股定理的内容?
2.勾股定理有什么作用?
3.阅读教科书、回看课件,总结勾股定理的其他证明方法.了解中国人的伟大和外国人的智慧.
Rt三角形的边长知二求一(线段长)
