2021-2022学年八年级数学人教版下册课件 17.1勾股定理 课件(共26张PPT)
文档属性
| 名称 | 2021-2022学年八年级数学人教版下册课件 17.1勾股定理 课件(共26张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 08:35:45 | ||
图片预览

文档简介
(共26张PPT)
勾
股
弦
读一读
勾股世界
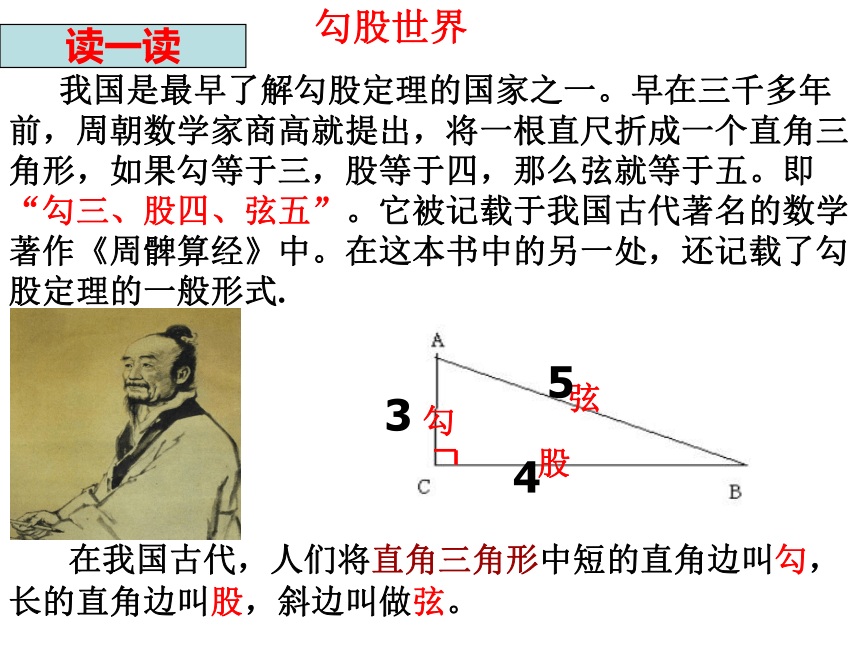
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式.
在我国古代,人们将直角三角形中短的直角边叫勾,长的直角边叫股,斜边叫做弦。
3
5
4
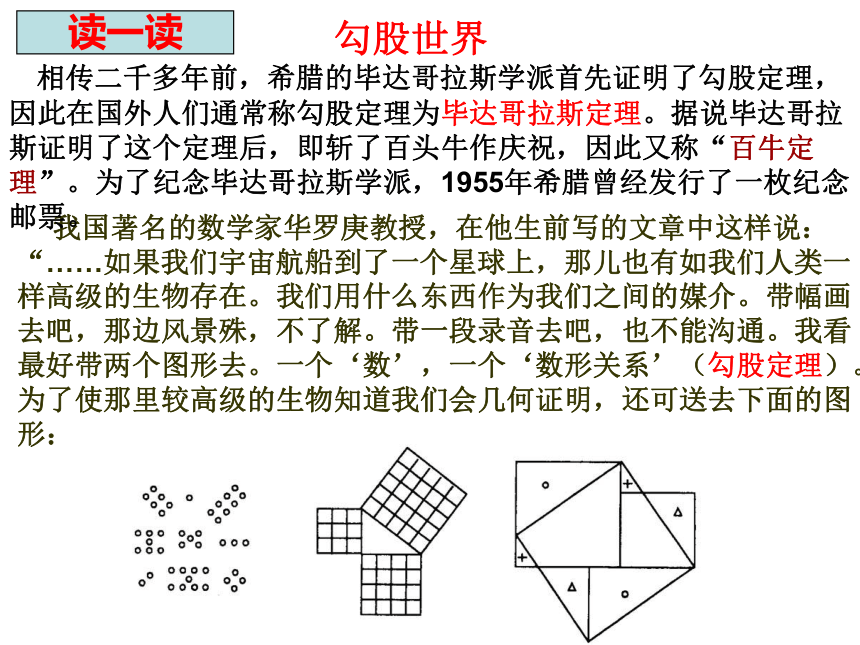
我国著名的数学家华罗庚教授,在他生前写的文章中这样说:“……如果我们宇宙航船到了一个星球上,那儿也有如我们人类一样高级的生物存在。我们用什么东西作为我们之间的媒介。带幅画去吧,那边风景殊,不了解。带一段录音去吧,也不能沟通。我看最好带两个图形去。一个‘数’,一个‘数形关系’(勾股定理)。为了使那里较高级的生物知道我们会几何证明,还可送去下面的图形:
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。据说毕达哥拉斯证明了这个定理后,即斩了百头牛作庆祝,因此又称“百牛定理”。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
勾股世界
读一读
活动 1
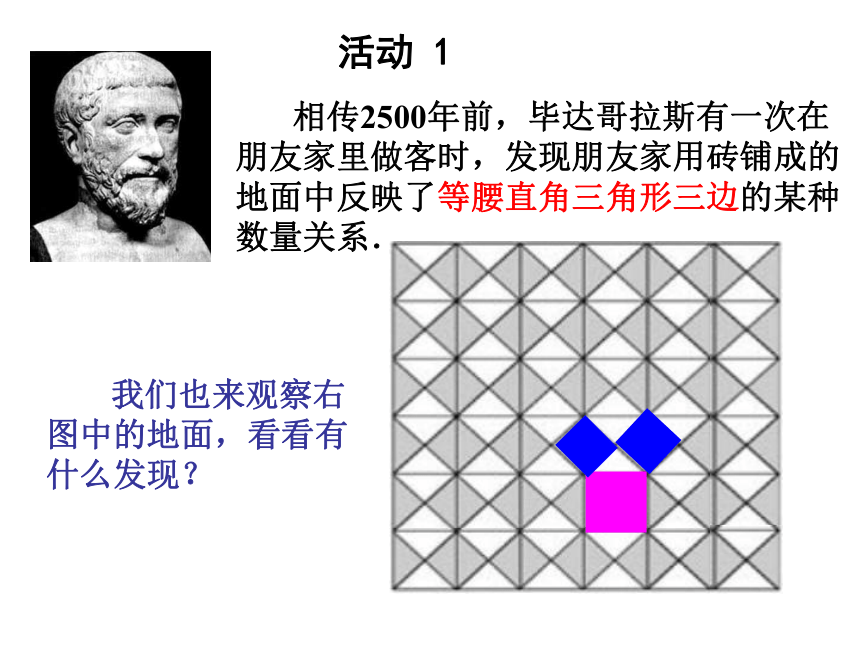
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了等腰直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
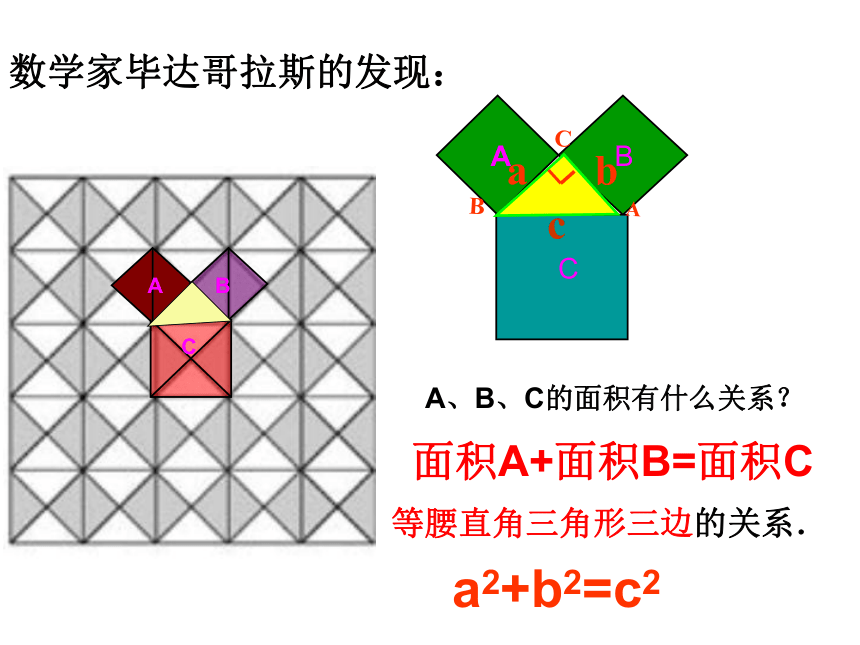
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
A
B
C
a
b
c
a2+b2=c2
面积A+面积B=面积C
A
B
C
等腰直角三角形三边的关系.
C
B
A
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
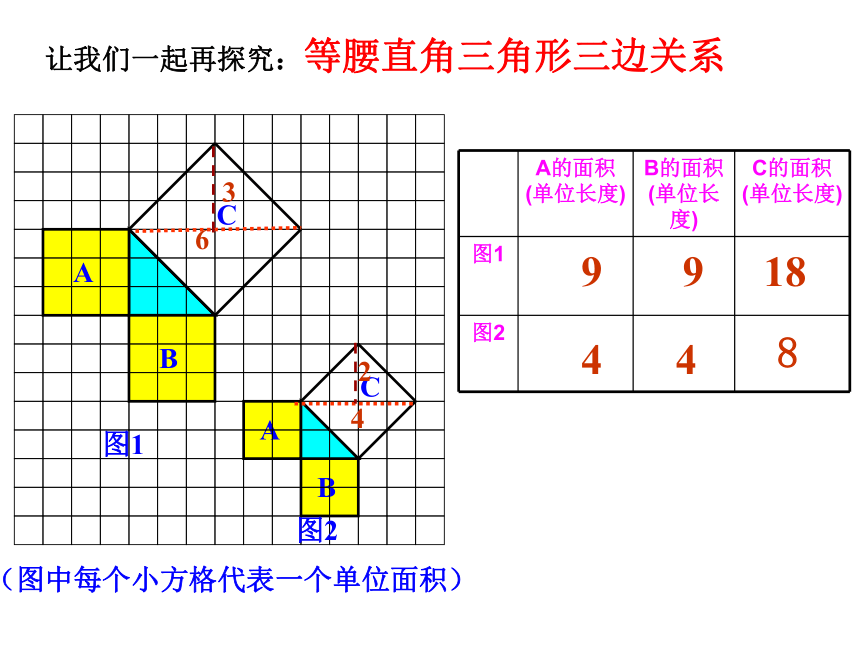
让我们一起再探究:等腰直角三角形三边关系
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
图2
9
9
18
4
4
8
6
3
4
2
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
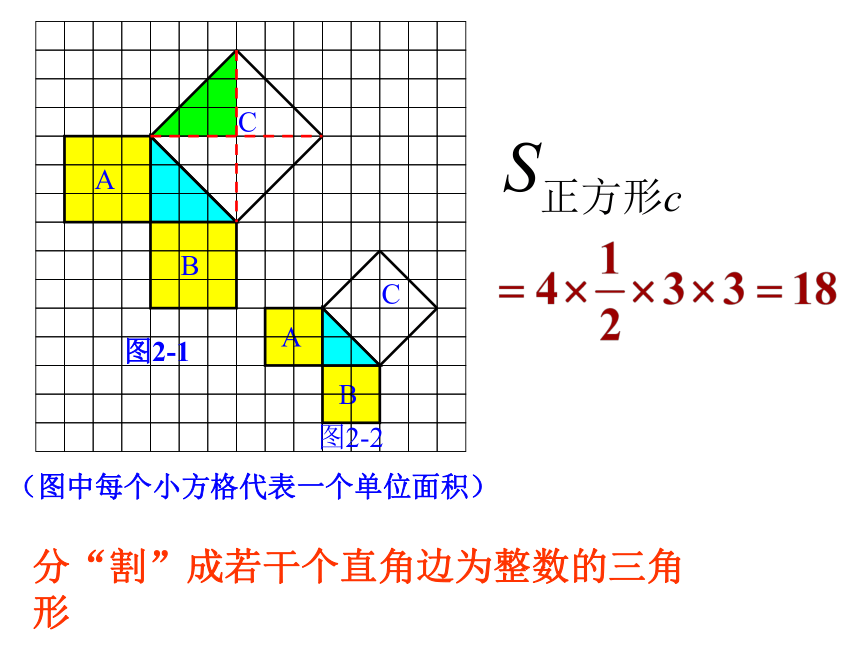
分“割”成若干个直角边为整数的三角形
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
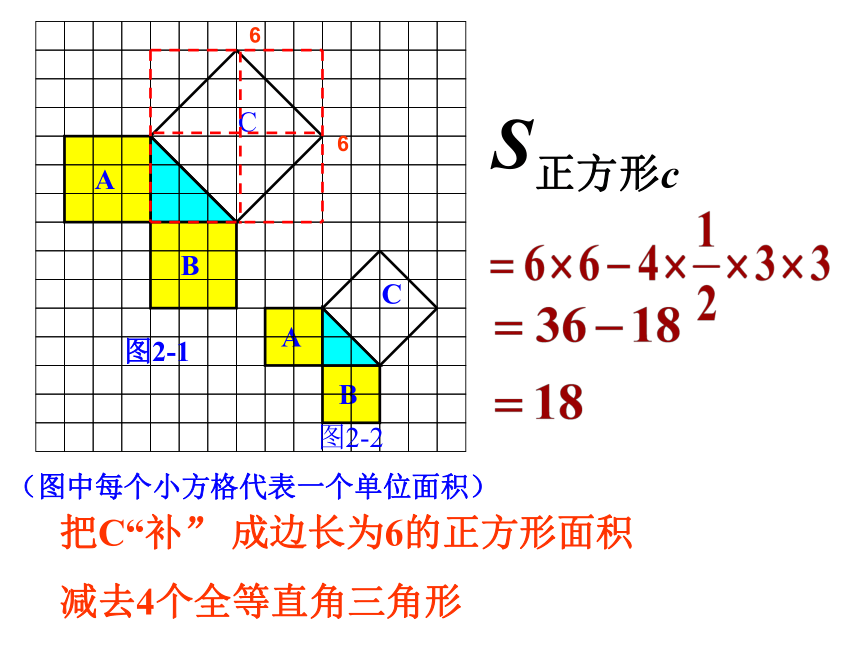
把C“补” 成边长为6的正方形面积
减去4个全等直角三角形
6
6
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
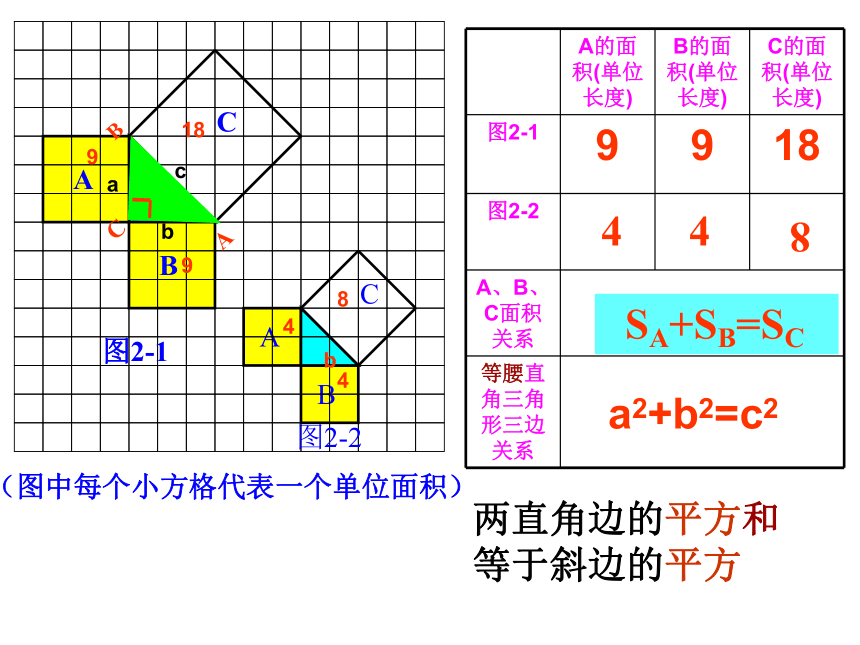
SA+SB=SC
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2-1 9 9 18
图2-2
A、B、C面积关系
等腰直角三角形三边关系
4
4
8
两直角边的平方和
等于斜边的平方
9
9
18
4
4
8
a2+b2=c2
a
b
b
c
C
A
B
A
B
C
图1-2
A
B
C
图1-3
2.观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1-2
图1-3
16
9
25
4
9
13
不是等腰的直角三角形会不会?
7
7
C1的面积=72-4×0.5×4×3
C2的面积=52-4×0.5×2×3
5
=49-24=25
=25-12=13
5
4
3
A
B
C
a
c
b
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2
+b2
=c2
两直角边的平方和等于斜边的平方
┏
a2+b2=c2
a
c
b
命题:如果直角三角形的两直角边长分别是a、b,斜边长是c,那么
推论:
赵爽的“弦图”
早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
c2
=
a2 + b2 = c2
可得:
c2 = a2-2ab+b2+2ab
b
c
a
想一想:图中有几个正方形?
证明一(面积法)
a
b
ab
(a-b)2+4×
s大正方形=s小正方形+4 s三角形
这就是本届大会会徽的图案.
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
s大正方形=s小正方形+4s三角形
美国第二十任总统伽菲尔德
总统巧证勾股定理
a
a
b
b
c
c
A
D
C
B
E
证明三
定理:经过证明被确认为正确的命题叫做定理。
勾股定理:
如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则 a2+b2=c2
A
B
C
股b
勾 a
弦c
勾2+股2=弦2
(1)使用前提是直角三角形
(2)分清直角边、斜边
使用时要注意什么?
勾股定理的各种表达式:
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
c2=a2+b2
a2=c2-b2
b2=c2-a2
正数c=
正数a=
正数b=
A
B
C
股b
勾 a
弦c
课堂例题:求出下列直角三角形中未知边x的长度
6
8
x
5
x
13
解:由勾股定理得:
x2 =36+64
x2 =100
x2=62+82
∴正数 x=10
x2=132-52
x2 =169-25
x2 =144
∴正数 x=12
解:由勾股定理得:
勾股定理的简单应用
1、如图中的各个直角三角形,求未知边的长。
3
4
A
B
C
?
12
?
13
E
F
G
解:
(1)在直角三角形ABC中
因为AC = AB + BC
2
2
2
(2)在直角三角形EFG中
因为GF = GE - EF
2
2
2
所以AC2=42+32=25
所以AC=5
所以GF2=132-122=25
所以GF=5
练习:
2、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
3.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
x2=81+144
x2=225
正数x=15
y2=169-144
y2=25
正数y=5
z2=625-576
z2=49
正数z=7
=4+6=10
=S5+S6
S7
y=0
借题发挥
4
6
10
S5=s1+s2=1+3=4
S6=s3+s4=2+4=6
D
A
B
C
4.蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
3
4
12
5
6
8
AB2=32+42=25
AB=5
BC2=122+52=169
BC=13
CD2=62+82=100
CD=10
路程=AB+BC+CD=28
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和,等于斜边c平方
a2+b2 =c2
⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长.
作业P21--22
勾
股
弦
读一读
勾股世界
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角三角形,如果勾等于三,股等于四,那么弦就等于五。即“勾三、股四、弦五”。它被记载于我国古代著名的数学著作《周髀算经》中。在这本书中的另一处,还记载了勾股定理的一般形式.
在我国古代,人们将直角三角形中短的直角边叫勾,长的直角边叫股,斜边叫做弦。
3
5
4
我国著名的数学家华罗庚教授,在他生前写的文章中这样说:“……如果我们宇宙航船到了一个星球上,那儿也有如我们人类一样高级的生物存在。我们用什么东西作为我们之间的媒介。带幅画去吧,那边风景殊,不了解。带一段录音去吧,也不能沟通。我看最好带两个图形去。一个‘数’,一个‘数形关系’(勾股定理)。为了使那里较高级的生物知道我们会几何证明,还可送去下面的图形:
相传二千多年前,希腊的毕达哥拉斯学派首先证明了勾股定理,因此在国外人们通常称勾股定理为毕达哥拉斯定理。据说毕达哥拉斯证明了这个定理后,即斩了百头牛作庆祝,因此又称“百牛定理”。为了纪念毕达哥拉斯学派,1955年希腊曾经发行了一枚纪念邮票。
勾股世界
读一读
活动 1
相传2500年前,毕达哥拉斯有一次在朋友家里做客时,发现朋友家用砖铺成的地面中反映了等腰直角三角形三边的某种数量关系.
我们也来观察右图中的地面,看看有什么发现?
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
A
B
C
a
b
c
a2+b2=c2
面积A+面积B=面积C
A
B
C
等腰直角三角形三边的关系.
C
B
A
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
让我们一起再探究:等腰直角三角形三边关系
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图1
图2
9
9
18
4
4
8
6
3
4
2
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
分“割”成若干个直角边为整数的三角形
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
把C“补” 成边长为6的正方形面积
减去4个全等直角三角形
6
6
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图2-1
图2-2
SA+SB=SC
A的面积(单位长度) B的面积(单位长度) C的面积(单位长度)
图2-1 9 9 18
图2-2
A、B、C面积关系
等腰直角三角形三边关系
4
4
8
两直角边的平方和
等于斜边的平方
9
9
18
4
4
8
a2+b2=c2
a
b
b
c
C
A
B
A
B
C
图1-2
A
B
C
图1-3
2.观察右边两个图并填写下表:
A的面积 B的面积 C的面积
图1-2
图1-3
16
9
25
4
9
13
不是等腰的直角三角形会不会?
7
7
C1的面积=72-4×0.5×4×3
C2的面积=52-4×0.5×2×3
5
=49-24=25
=25-12=13
5
4
3
A
B
C
a
c
b
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2
+b2
=c2
两直角边的平方和等于斜边的平方
┏
a2+b2=c2
a
c
b
命题:如果直角三角形的两直角边长分别是a、b,斜边长是c,那么
推论:
赵爽的“弦图”
早在公元3世纪,我国数学家赵爽就用左边的图形验证了“勾股定理”
(4)
(3)
(2)
(1)
(1)
(2)
(3)
(4)
c
c
c
c
(a-b)2
c2
=
a2 + b2 = c2
可得:
c2 = a2-2ab+b2+2ab
b
c
a
想一想:图中有几个正方形?
证明一(面积法)
a
b
ab
(a-b)2+4×
s大正方形=s小正方形+4 s三角形
这就是本届大会会徽的图案.
b
a
b
a
b
a
b
a
c
c
c
c
大正方形的面积该怎样表示
(a+b)2
=
a2 + b2 + 2ab = c2+2ab
可得: a2 + b2 = c2
证明二
s大正方形=s小正方形+4s三角形
美国第二十任总统伽菲尔德
总统巧证勾股定理
a
a
b
b
c
c
A
D
C
B
E
证明三
定理:经过证明被确认为正确的命题叫做定理。
勾股定理:
如果直角三角形的两直角边长分别为 a、b,斜边为c,那么a2+b2=c2。
如图,在Rt△ABC中,∠C= 90°,则 a2+b2=c2
A
B
C
股b
勾 a
弦c
勾2+股2=弦2
(1)使用前提是直角三角形
(2)分清直角边、斜边
使用时要注意什么?
勾股定理的各种表达式:
在RT△ABC中,∠C=90°, ∠A 、∠B、 ∠C的对边分别为a 、b 、c ,则:
c2=a2+b2
a2=c2-b2
b2=c2-a2
正数c=
正数a=
正数b=
A
B
C
股b
勾 a
弦c
课堂例题:求出下列直角三角形中未知边x的长度
6
8
x
5
x
13
解:由勾股定理得:
x2 =36+64
x2 =100
x2=62+82
∴正数 x=10
x2=132-52
x2 =169-25
x2 =144
∴正数 x=12
解:由勾股定理得:
勾股定理的简单应用
1、如图中的各个直角三角形,求未知边的长。
3
4
A
B
C
?
12
?
13
E
F
G
解:
(1)在直角三角形ABC中
因为AC = AB + BC
2
2
2
(2)在直角三角形EFG中
因为GF = GE - EF
2
2
2
所以AC2=42+32=25
所以AC=5
所以GF2=132-122=25
所以GF=5
练习:
2、求下列图中字母所表示的正方形的面积
=625
225
400
A
225
81
B
=144
3.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
x2=81+144
x2=225
正数x=15
y2=169-144
y2=25
正数y=5
z2=625-576
z2=49
正数z=7
=4+6=10
=S5+S6
S7
y=0
借题发挥
4
6
10
S5=s1+s2=1+3=4
S6=s3+s4=2+4=6
D
A
B
C
4.蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)
G
F
E
3
4
12
5
6
8
AB2=32+42=25
AB=5
BC2=122+52=169
BC=13
CD2=62+82=100
CD=10
路程=AB+BC+CD=28
⒈ 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系.
⒉勾股定理: 直角三角形两直角边a、b平方和,等于斜边c平方
a2+b2 =c2
⒊勾股定理的主要作用是:
在直角三角形中,已知任意两边求第三边的长.
作业P21--22
