2021-2022学年人教版七年级数学下册《5.3平行线的性质》同步自主提升训练(Word版 附答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册《5.3平行线的性质》同步自主提升训练(Word版 附答案) |  | |
| 格式 | doc | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 19:29:16 | ||
图片预览



文档简介
2021-2022学年人教版七年级数学下册《5-3平行线的性质》同步自主提升训练(附答案)
1.如图,已知直线AB∥CD,分别交直线EF于E、F两点,点M为直线EF左边一点,且∠BEM=150°,∠EMF=35°,则∠CFM的度数为 .
2.如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
(1)∠1、∠2、∠3之间的关系为 ;
(2)如果点P在A、B两点之间运动时,∠1、∠2、∠3之间的关系为 ;
(3)如果点P(点P和A、B不重合)在A、B两点外侧运动时,∠1、∠2、∠3之间关系为 .
3.如图,已知AB∥CD,OE平分∠AOD,OF⊥OE,∠CDO=50°,则∠DOF= 度.
4.如图,直线a∥b,∠1=28°,∠2=50°,则∠3= 度,∠3+∠4+∠5= 度.
5.如图,已知AB∥CD,则∠A、∠C、∠P的关系为 .
6.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .
7.如图,已知AD∥BC,BD 平分∠ABC,∠A=112°,且BD⊥CD,则∠ADC= .
8.如图,直线a∥b,若∠1=60°,则∠2= 度.
9.如图,若过点P1,P2作直线m的平行线,则∠1、∠2、∠3、∠4间的数量关系是 .
10.如图,直线AB∥CD,EF分别与AB、CD相交,如果∠1=60°,那么∠2的度数 .
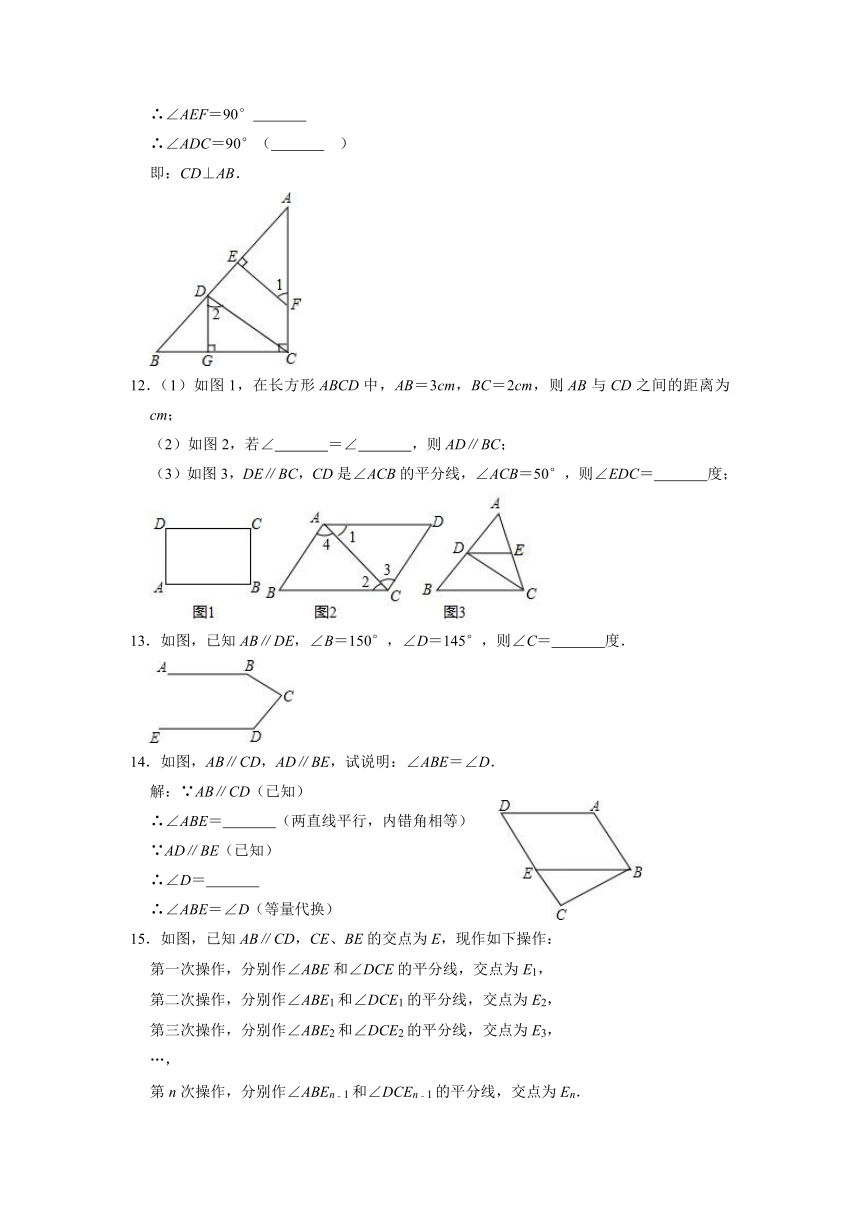
11.如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.
解:∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠ =90°(垂直的定义)
∴DG∥
∴∠2=∠
∵∠1= ( 已知 )
∴∠1=∠
∴EF∥
∴∠AEF=∠ ( )
∵EF⊥AB
∴∠AEF=90°
∴∠ADC=90°( )
即:CD⊥AB.
12.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为 cm;
(2)如图2,若∠ =∠ ,则AD∥BC;
(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC= 度;
13.如图,已知AB∥DE,∠B=150°,∠D=145°,则∠C= 度.
14.如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
解:∵AB∥CD(已知)
∴∠ABE= (两直线平行,内错角相等)
∵AD∥BE(已知)
∴∠D=
∴∠ABE=∠D(等量代换)
15.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,
…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
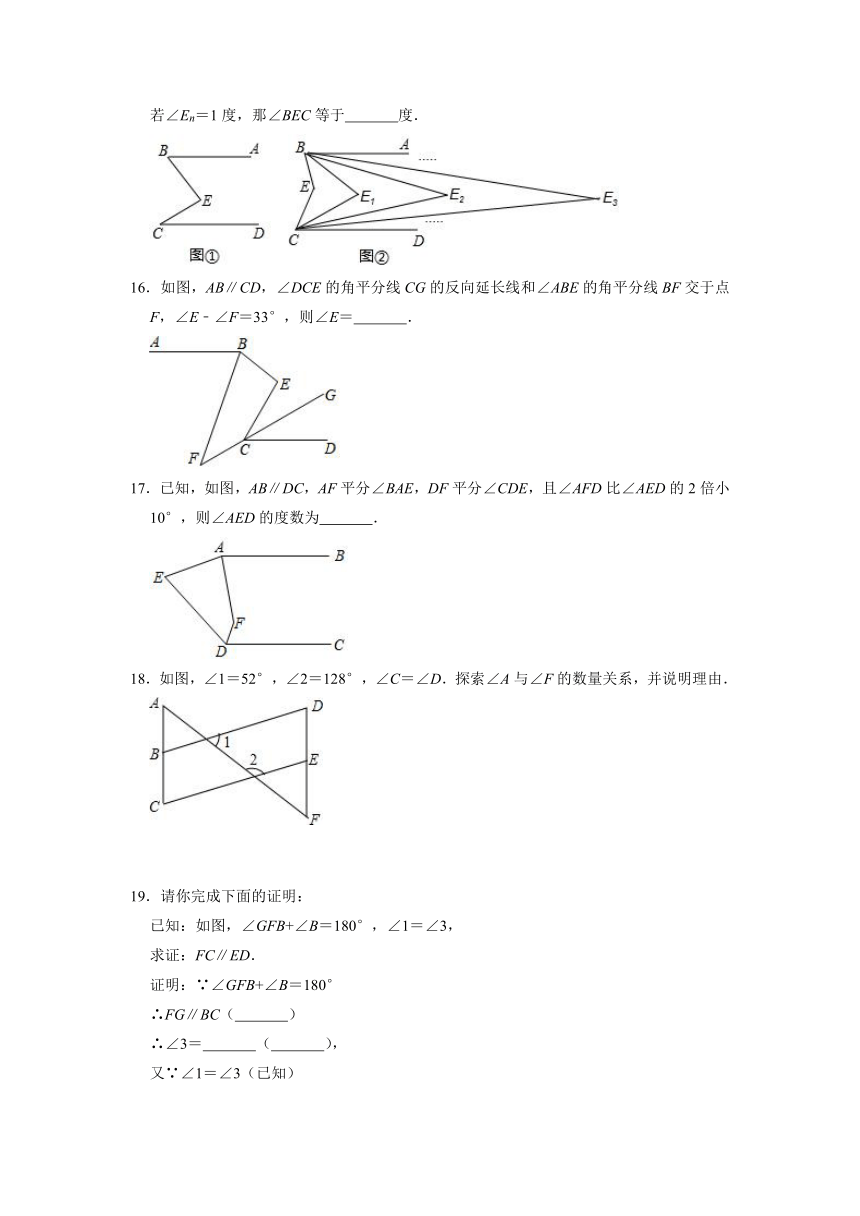
若∠En=1度,那∠BEC等于 度.
16.如图,AB∥CD,∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,∠E﹣∠F=33°,则∠E= .
17.已知,如图,AB∥DC,AF平分∠BAE,DF平分∠CDE,且∠AFD比∠AED的2倍小10°,则∠AED的度数为 .
18.如图,∠1=52°,∠2=128°,∠C=∠D.探索∠A与∠F的数量关系,并说明理由.
19.请你完成下面的证明:
已知:如图,∠GFB+∠B=180°,∠1=∠3,
求证:FC∥ED.
证明:∵∠GFB+∠B=180°
∴FG∥BC( )
∴∠3= ( ),
又∵∠1=∠3(已知)
∴∠1= (等量代换)
∴FC∥ED( )
20.如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )
参考答案
1.解:延长EM交直线CD于点G,
∵直线AB∥CD,∠BEM=150°,
∴∠MGF=180°﹣150°=30°.
∵∠EMF是△GMF的外角,∠EMF=35°,
∴∠CFM=∠EMF﹣∠MGF=35°﹣30°=5°.
故答案为:5°.
2.证明:(1)如图1,过点P作PQ∥l1,
∵PQ∥l1,
∴∠1=∠4(两直线平行,内错角相等),
∵PQ∥l1,l1∥l2(已知),
∴PQ∥l2(平行于同一条直线的两直线平行),
∴∠5=∠2(两直线平行,内错角相等),
∵∠3=∠4+∠5,
∴∠3=∠1+∠2(等量代换);
故答案为:∠3=∠1+∠2;
(2)∠1、∠2、∠3之间的关系不发生变化;
故答案为:∠3=∠1+∠2;
(3)∠1﹣∠2=∠3或∠2﹣∠1=∠3.
故答案为:∠1﹣∠2=∠3或∠2﹣∠1=∠3.
3.解:∵AB∥CD,OE平分∠AOD,∠CDO=50°,
∴∠AOD=180°﹣∠CDO=180°﹣50°=130°,
∠AOE=∠DOE=∠AOD=×130°=65°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠DOF=∠EOF﹣∠DOE=90°﹣65°=25°.
4.解:如图所示:过∠3的顶点作c∥a,
∵a∥b,
∴a∥b∥c,
∴∠1=∠6,∠7=∠2,
又∠3=∠6+∠7,
∴∠3=∠1+∠2=78°;
又∠4+∠6=∠7+∠5=180°
∴∠3+∠4+∠5=360°.
5.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
6.解:∵AD∥BC,
∴∠2=∠DEG,∠EFG=∠DEF=49°,
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G,
∴∠DEF=∠GEF=49°,
∴∠2=2×49°=98°,
∴∠1=180°﹣98°=82°,
∴∠2﹣∠1=98°﹣82°=16°.
故答案为16°.
7.解:∵AD∥BC,∠A=112°,
∴∠ABC=180°﹣∠A=68°,
∵BD 平分∠ABC,
∴∠CBD=∠ABC=34°,
∵BD⊥CD,
∴∠C=90°﹣∠CBD=56°,
∴∠ADC=180°﹣∠C=124°.
故答案为:124°.
8.解:∵a∥b,
∴∠2=∠1,
∵∠1=60°,
∴∠2=60°.
故答案为60.
9.解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,
∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
10.解:∵∠1=60°,∠1与∠3是对顶角,
∴∠3=∠1=60°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣60°=120°.
故答案为:120°.
11.解:∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠BCA=90°(垂直的定义)
∴DG∥AC,
∴∠2=∠DCA,
∵∠1=∠2( 已知 ),
∴∠1=∠DCA,
∴EF∥DC,
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义),
∴∠ADC=90°(等量代换),
即:CD⊥AB,
故答案为:BCA,AC,DCA,∠2,DCA,DC,ADC,两直线平行,同位角相等,(已知),(垂直定义),等量代换.
12.解:(1)已知四边形ABCD为长方形,则AB∥CD,∠C=90°,∠B=90°.
又BC=2cm,故AB与CD之间的距离为2cm.
故填2.
(2)要使AD∥BC,根据平行线的判定定理可得∠1=∠2.
故填∠1;∠2.
(3)已知DE∥BC,
根据平行线判定定理可得∠EDC=∠DCB,
又CD是∠ACB的平分线,
∴∠ECD=∠DCB,
∵∠ACB=50°,
∴∠EDC=25°.
故填25.
13.解:过点C作CF平行于AB,如图:
∵AB∥DE,
∴AB∥CF∥ED.
AB∥CF ∠1=180°﹣∠B=30°,
CF∥ED ∠2=180°﹣∠D=35°,
∴∠BCD=∠1+∠2=65°.
故填65°.
14.解:∵AB∥CD(已知)
∴∠ABE=∠BEC(两直线平行,内错角相等)
∵AD∥BE(已知)
∴∠D=∠BEC,
∴∠ABE=∠D(等量代换).
故答案为:∠BEC,∠BEC.
15.解:如图①,过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
如图②,∵∠ABE和∠DCE的平分线交点为E1,
∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC.
∵∠ABE1和∠DCE1的平分线交点为E2,
∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;
如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;
…
以此类推,∠En=∠BEC.
∴当∠En=1度时,∠BEC等于2n度.
故答案为:2n.
16.解:如图,过F作FH∥AB,
∵AB∥CD,
∴FH∥AB∥CD,
∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,
∴可设∠ABF=∠EBF=α=∠BFH,∠DCG=∠ECG=β=∠CFH,
∴∠ECF=180°﹣β,∠BFC=∠BFH﹣∠CFH=α﹣β,
∴四边形BFCE中,∠E+∠BFC=360°﹣α﹣(180°﹣β)=180°﹣(α﹣β)=180°﹣∠BFC,
即∠E+2∠BFC=180°,①
又∵∠E﹣∠BFC=33°,
∴∠BFC=∠E﹣33°,②
∴由①②可得,∠E+2(∠E﹣33°)=180°,
解得∠E=82°,
故答案为:82°.
17.解:如图所示,过F作FG∥AB,
∵AB∥DC,
∴AB∥GF∥CD,
∴∠1=∠DFG,∠2=∠AFG,
∴∠AFD=∠1+∠2,
∵AF平分∠BAE,DF平分∠CDE,
∴∠1=∠3,∠2=∠4,
设∠E=α,则∠AFD=2α﹣10°,
∴∠AFD=∠3+∠4=2α﹣10°,
∵四边形AEDF中,∠E+∠3+∠4+∠AFD=360°,
∴α+2(2α﹣10°)=360°,
解得α=76°,
故答案为:76°.
18.解:∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF,
∴∠A=∠F.
19.证明:∵∠GFB+∠B=180°
∴FG∥BC(同旁内角互补,两直线平行)
∴∠3=∠2(两直线平行,内错角相等),
又∵∠1=∠3(已知)
∴∠1=∠2(等量代换)
∴FC∥ED(同位角相等,两直线平行);
故答案为:同旁内角互补,两直线平行;∠2;两直线平行,内错角相等;∠2;同位角相等,两直线平行.
20.解:∵∠1+∠2=180°,(已知)
∠1=∠4,(对顶角相等)
∴∠2+∠4=180°,
∴EH∥AB,(同旁内角互补,两直线平行)
∴∠B=∠EHC,(两直线平行,同位角相等)
∵∠3=∠B,(已知)
∴∠3=∠EHC,(等量代换)
∴DE∥BC,(内错角相等,两直线平行)
故答案为:对顶角相等;同旁内角互补,两直线平行;EHC;两直线平行,同位角相等;内错角相等,两直线平行.
1.如图,已知直线AB∥CD,分别交直线EF于E、F两点,点M为直线EF左边一点,且∠BEM=150°,∠EMF=35°,则∠CFM的度数为 .
2.如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
(1)∠1、∠2、∠3之间的关系为 ;
(2)如果点P在A、B两点之间运动时,∠1、∠2、∠3之间的关系为 ;
(3)如果点P(点P和A、B不重合)在A、B两点外侧运动时,∠1、∠2、∠3之间关系为 .
3.如图,已知AB∥CD,OE平分∠AOD,OF⊥OE,∠CDO=50°,则∠DOF= 度.
4.如图,直线a∥b,∠1=28°,∠2=50°,则∠3= 度,∠3+∠4+∠5= 度.
5.如图,已知AB∥CD,则∠A、∠C、∠P的关系为 .
6.把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=49°,则∠2﹣∠1= .
7.如图,已知AD∥BC,BD 平分∠ABC,∠A=112°,且BD⊥CD,则∠ADC= .
8.如图,直线a∥b,若∠1=60°,则∠2= 度.
9.如图,若过点P1,P2作直线m的平行线,则∠1、∠2、∠3、∠4间的数量关系是 .
10.如图,直线AB∥CD,EF分别与AB、CD相交,如果∠1=60°,那么∠2的度数 .
11.如图,已知DG⊥BC,BC⊥AC,EF⊥AB,∠1=∠2,试判断CD与AB的位置关系.
解:∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠ =90°(垂直的定义)
∴DG∥
∴∠2=∠
∵∠1= ( 已知 )
∴∠1=∠
∴EF∥
∴∠AEF=∠ ( )
∵EF⊥AB
∴∠AEF=90°
∴∠ADC=90°( )
即:CD⊥AB.
12.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为 cm;
(2)如图2,若∠ =∠ ,则AD∥BC;
(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC= 度;
13.如图,已知AB∥DE,∠B=150°,∠D=145°,则∠C= 度.
14.如图,AB∥CD,AD∥BE,试说明:∠ABE=∠D.
解:∵AB∥CD(已知)
∴∠ABE= (两直线平行,内错角相等)
∵AD∥BE(已知)
∴∠D=
∴∠ABE=∠D(等量代换)
15.如图,已知AB∥CD,CE、BE的交点为E,现作如下操作:
第一次操作,分别作∠ABE和∠DCE的平分线,交点为E1,
第二次操作,分别作∠ABE1和∠DCE1的平分线,交点为E2,
第三次操作,分别作∠ABE2和∠DCE2的平分线,交点为E3,
…,
第n次操作,分别作∠ABEn﹣1和∠DCEn﹣1的平分线,交点为En.
若∠En=1度,那∠BEC等于 度.
16.如图,AB∥CD,∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,∠E﹣∠F=33°,则∠E= .
17.已知,如图,AB∥DC,AF平分∠BAE,DF平分∠CDE,且∠AFD比∠AED的2倍小10°,则∠AED的度数为 .
18.如图,∠1=52°,∠2=128°,∠C=∠D.探索∠A与∠F的数量关系,并说明理由.
19.请你完成下面的证明:
已知:如图,∠GFB+∠B=180°,∠1=∠3,
求证:FC∥ED.
证明:∵∠GFB+∠B=180°
∴FG∥BC( )
∴∠3= ( ),
又∵∠1=∠3(已知)
∴∠1= (等量代换)
∴FC∥ED( )
20.如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )
参考答案
1.解:延长EM交直线CD于点G,
∵直线AB∥CD,∠BEM=150°,
∴∠MGF=180°﹣150°=30°.
∵∠EMF是△GMF的外角,∠EMF=35°,
∴∠CFM=∠EMF﹣∠MGF=35°﹣30°=5°.
故答案为:5°.
2.证明:(1)如图1,过点P作PQ∥l1,
∵PQ∥l1,
∴∠1=∠4(两直线平行,内错角相等),
∵PQ∥l1,l1∥l2(已知),
∴PQ∥l2(平行于同一条直线的两直线平行),
∴∠5=∠2(两直线平行,内错角相等),
∵∠3=∠4+∠5,
∴∠3=∠1+∠2(等量代换);
故答案为:∠3=∠1+∠2;
(2)∠1、∠2、∠3之间的关系不发生变化;
故答案为:∠3=∠1+∠2;
(3)∠1﹣∠2=∠3或∠2﹣∠1=∠3.
故答案为:∠1﹣∠2=∠3或∠2﹣∠1=∠3.
3.解:∵AB∥CD,OE平分∠AOD,∠CDO=50°,
∴∠AOD=180°﹣∠CDO=180°﹣50°=130°,
∠AOE=∠DOE=∠AOD=×130°=65°.
∵OF⊥OE,
∴∠EOF=90°.
∴∠DOF=∠EOF﹣∠DOE=90°﹣65°=25°.
4.解:如图所示:过∠3的顶点作c∥a,
∵a∥b,
∴a∥b∥c,
∴∠1=∠6,∠7=∠2,
又∠3=∠6+∠7,
∴∠3=∠1+∠2=78°;
又∠4+∠6=∠7+∠5=180°
∴∠3+∠4+∠5=360°.
5.解:如右图所示,作PE∥CD,
∵PE∥CD,
∴∠C+∠CPE=180°,
又∵AB∥CD,
∴PE∥AB,
∴∠A=∠APE,
∴∠A+∠C﹣∠P=180°,
故答案为:∠A+∠C﹣∠P=180°.
6.解:∵AD∥BC,
∴∠2=∠DEG,∠EFG=∠DEF=49°,
∵长方形纸片ABCD沿EF折叠后ED与BC的交点为G,
∴∠DEF=∠GEF=49°,
∴∠2=2×49°=98°,
∴∠1=180°﹣98°=82°,
∴∠2﹣∠1=98°﹣82°=16°.
故答案为16°.
7.解:∵AD∥BC,∠A=112°,
∴∠ABC=180°﹣∠A=68°,
∵BD 平分∠ABC,
∴∠CBD=∠ABC=34°,
∵BD⊥CD,
∴∠C=90°﹣∠CBD=56°,
∴∠ADC=180°﹣∠C=124°.
故答案为:124°.
8.解:∵a∥b,
∴∠2=∠1,
∵∠1=60°,
∴∠2=60°.
故答案为60.
9.解:分别过点P1、P2作P1C∥m,P2D∥m,
∵m∥n,
∴P1C∥P2D∥m∥n,
∴∠1=∠AP1C,CP1P2=∠P1P2D,∠DP2B=∠4,
∴∠1+∠P1P2D+∠DP2B=∠AP1C+∠CP1P2+∠4,即∠2+∠4=∠1+∠3.
故答案为:∠2+∠4=∠1+∠3.
10.解:∵∠1=60°,∠1与∠3是对顶角,
∴∠3=∠1=60°,
∵AB∥CD,
∴∠2=180°﹣∠3=180°﹣60°=120°.
故答案为:120°.
11.解:∵DG⊥BC,BC⊥AC(已知)
∴∠DGB=∠BCA=90°(垂直的定义)
∴DG∥AC,
∴∠2=∠DCA,
∵∠1=∠2( 已知 ),
∴∠1=∠DCA,
∴EF∥DC,
∴∠AEF=∠ADC(两直线平行,同位角相等),
∵EF⊥AB(已知),
∴∠AEF=90°(垂直定义),
∴∠ADC=90°(等量代换),
即:CD⊥AB,
故答案为:BCA,AC,DCA,∠2,DCA,DC,ADC,两直线平行,同位角相等,(已知),(垂直定义),等量代换.
12.解:(1)已知四边形ABCD为长方形,则AB∥CD,∠C=90°,∠B=90°.
又BC=2cm,故AB与CD之间的距离为2cm.
故填2.
(2)要使AD∥BC,根据平行线的判定定理可得∠1=∠2.
故填∠1;∠2.
(3)已知DE∥BC,
根据平行线判定定理可得∠EDC=∠DCB,
又CD是∠ACB的平分线,
∴∠ECD=∠DCB,
∵∠ACB=50°,
∴∠EDC=25°.
故填25.
13.解:过点C作CF平行于AB,如图:
∵AB∥DE,
∴AB∥CF∥ED.
AB∥CF ∠1=180°﹣∠B=30°,
CF∥ED ∠2=180°﹣∠D=35°,
∴∠BCD=∠1+∠2=65°.
故填65°.
14.解:∵AB∥CD(已知)
∴∠ABE=∠BEC(两直线平行,内错角相等)
∵AD∥BE(已知)
∴∠D=∠BEC,
∴∠ABE=∠D(等量代换).
故答案为:∠BEC,∠BEC.
15.解:如图①,过E作EF∥AB,
∵AB∥CD,
∴AB∥EF∥CD,
∴∠B=∠1,∠C=∠2,
∵∠BEC=∠1+∠2,
∴∠BEC=∠ABE+∠DCE;
如图②,∵∠ABE和∠DCE的平分线交点为E1,
∴∠CE1B=∠ABE1+∠DCE1=∠ABE+∠DCE=∠BEC.
∵∠ABE1和∠DCE1的平分线交点为E2,
∴∠BE2C=∠ABE2+∠DCE2=∠ABE1+∠DCE1=∠CE1B=∠BEC;
如图②,∵∠ABE2和∠DCE2的平分线,交点为E3,
∴∠BE3C=∠ABE3+∠DCE3=∠ABE2+∠DCE2=∠CE2B=∠BEC;
…
以此类推,∠En=∠BEC.
∴当∠En=1度时,∠BEC等于2n度.
故答案为:2n.
16.解:如图,过F作FH∥AB,
∵AB∥CD,
∴FH∥AB∥CD,
∵∠DCE的角平分线CG的反向延长线和∠ABE的角平分线BF交于点F,
∴可设∠ABF=∠EBF=α=∠BFH,∠DCG=∠ECG=β=∠CFH,
∴∠ECF=180°﹣β,∠BFC=∠BFH﹣∠CFH=α﹣β,
∴四边形BFCE中,∠E+∠BFC=360°﹣α﹣(180°﹣β)=180°﹣(α﹣β)=180°﹣∠BFC,
即∠E+2∠BFC=180°,①
又∵∠E﹣∠BFC=33°,
∴∠BFC=∠E﹣33°,②
∴由①②可得,∠E+2(∠E﹣33°)=180°,
解得∠E=82°,
故答案为:82°.
17.解:如图所示,过F作FG∥AB,
∵AB∥DC,
∴AB∥GF∥CD,
∴∠1=∠DFG,∠2=∠AFG,
∴∠AFD=∠1+∠2,
∵AF平分∠BAE,DF平分∠CDE,
∴∠1=∠3,∠2=∠4,
设∠E=α,则∠AFD=2α﹣10°,
∴∠AFD=∠3+∠4=2α﹣10°,
∵四边形AEDF中,∠E+∠3+∠4+∠AFD=360°,
∴α+2(2α﹣10°)=360°,
解得α=76°,
故答案为:76°.
18.解:∵∠1=52°,∠2=128°,
∴∠1+∠2=180°,
∴BD∥CE,
∴∠C=∠ABD,
∵∠C=∠D,
∴∠D=∠ABD,
∴AC∥DF,
∴∠A=∠F.
19.证明:∵∠GFB+∠B=180°
∴FG∥BC(同旁内角互补,两直线平行)
∴∠3=∠2(两直线平行,内错角相等),
又∵∠1=∠3(已知)
∴∠1=∠2(等量代换)
∴FC∥ED(同位角相等,两直线平行);
故答案为:同旁内角互补,两直线平行;∠2;两直线平行,内错角相等;∠2;同位角相等,两直线平行.
20.解:∵∠1+∠2=180°,(已知)
∠1=∠4,(对顶角相等)
∴∠2+∠4=180°,
∴EH∥AB,(同旁内角互补,两直线平行)
∴∠B=∠EHC,(两直线平行,同位角相等)
∵∠3=∠B,(已知)
∴∠3=∠EHC,(等量代换)
∴DE∥BC,(内错角相等,两直线平行)
故答案为:对顶角相等;同旁内角互补,两直线平行;EHC;两直线平行,同位角相等;内错角相等,两直线平行.
