2021-2022学年鲁教版八年级数学下册《6.3正方形的性质与判定》同步达标测试(Word版 附答案)
文档属性
| 名称 | 2021-2022学年鲁教版八年级数学下册《6.3正方形的性质与判定》同步达标测试(Word版 附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 256.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 19:40:53 | ||
图片预览


文档简介
2021-2022学年鲁教版八年级数学下册《6-3正方形的性质与判定》同步达标测试(附答案)
一.选择题(共10小题,满分40分)
1.正方形具备而菱形不具备的性质是( )
A.四条边都相等 B.四个角都是直角
C.对角线互相垂直平分 D.每条对角线平分一组对角
2.正方形ABCD的一条对角线长为2,则正方形ABCD的周长为( )
A.4 B.8 C.2 D.4
3.如图,正方形ABCD中,延长AB至E,使AE=AC,连接CE,则∠BCE=( )
A.10° B.20° C.30° D.22.5°
4.已知四边形ABCD是平行四边形,则下列结论中正确的是( )
A.当AB⊥BD时,它是菱形 B.当AC=BD时,它是正方形
C.当∠ABC=90°时,它是矩形 D.当AB=BC时,它是矩形
5.如图,将一个正方形剪去一个角后,∠1+∠2等于( )
A.120° B.170° C.220° D.270°
6.如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
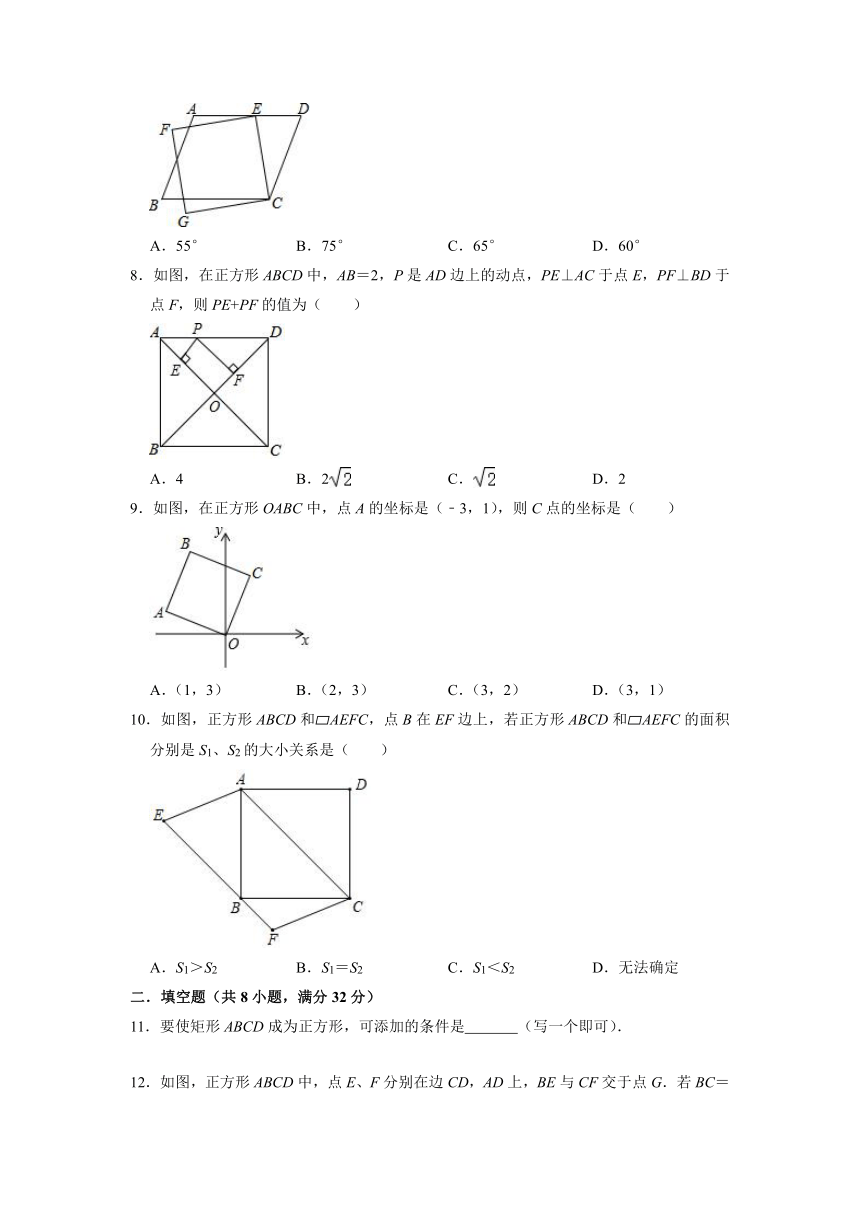
7.如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上.若∠ECD=43°,∠AEF=28°,则∠B的度数为( )
A.55° B.75° C.65° D.60°
8.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
9.如图,在正方形OABC中,点A的坐标是(﹣3,1),则C点的坐标是( )
A.(1,3) B.(2,3) C.(3,2) D.(3,1)
10.如图,正方形ABCD和 AEFC,点B在EF边上,若正方形ABCD和 AEFC的面积分别是S1、S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
二.填空题(共8小题,满分32分)
11.要使矩形ABCD成为正方形,可添加的条件是 (写一个即可).
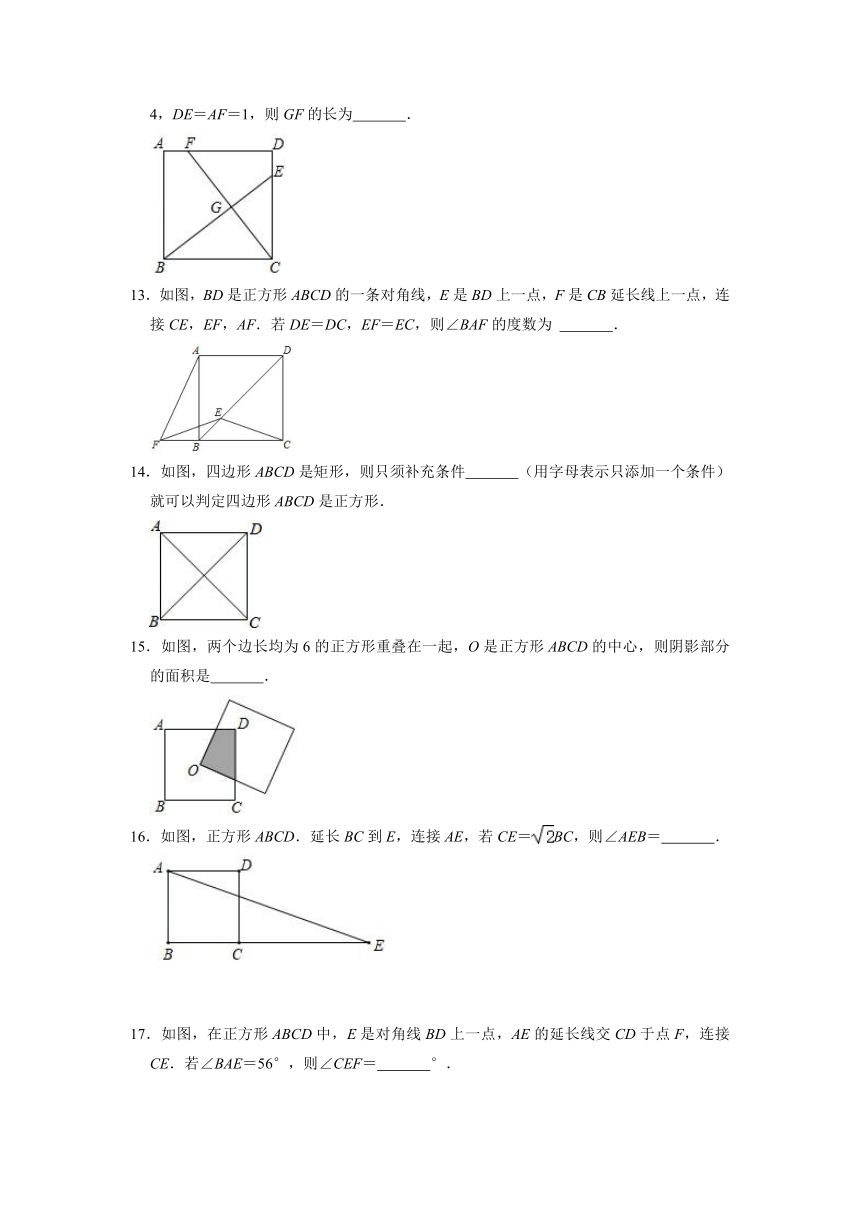
12.如图,正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为 .
13.如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE,EF,AF.若DE=DC,EF=EC,则∠BAF的度数为 .
14.如图,四边形ABCD是矩形,则只须补充条件 (用字母表示只添加一个条件)就可以判定四边形ABCD是正方形.
15.如图,两个边长均为6的正方形重叠在一起,O是正方形ABCD的中心,则阴影部分的面积是 .
16.如图,正方形ABCD.延长BC到E,连接AE,若CE=BC,则∠AEB= .
17.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
18.如图,正方形ABCD的边长为2,M是BC的中点,N是AM上的动点,过点N作EF⊥AM分别交AB,CD于点E,F.
(1)AM的长为 ;
(2)EM+AF的最小值为 .
三.解答题(共6小题)
19.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)证明:△ADE≌△CBF.
(2)若AB=4,AE=2,求四边形BEDF的周长.
20.如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
21.如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F.
(1)求证:AE=EF;
(2)若S△CEF=2,求EF的长.
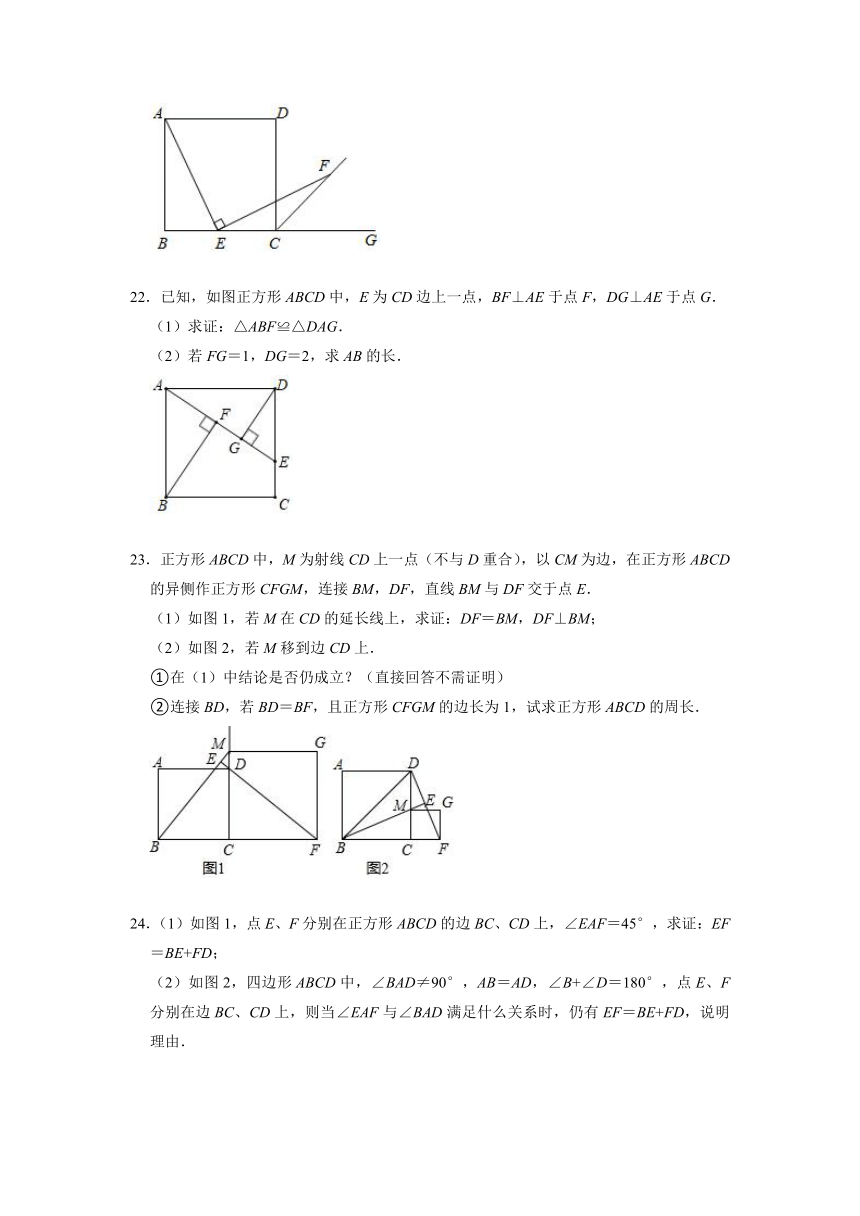
22.已知,如图正方形ABCD中,E为CD边上一点,BF⊥AE于点F,DG⊥AE于点G.
(1)求证:△ABF≌△DAG.
(2)若FG=1,DG=2,求AB的长.
23.正方形ABCD中,M为射线CD上一点(不与D重合),以CM为边,在正方形ABCD的异侧作正方形CFGM,连接BM,DF,直线BM与DF交于点E.
(1)如图1,若M在CD的延长线上,求证:DF=BM,DF⊥BM;
(2)如图2,若M移到边CD上.
①在(1)中结论是否仍成立?(直接回答不需证明)
②连接BD,若BD=BF,且正方形CFGM的边长为1,试求正方形ABCD的周长.
24.(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:A、正方形和菱形均具有,故不正确;
B、菱形的四个角相等但不一定是直角,故正确;
C、正方形和菱形均具有此性质,故不正确;
D、正方形和菱形均具有此性质,故不正确;
故选:B.
2.解:因为正方形ABCD的一条对角线长为2,
设正方形的边长为a,
根据勾股定理,得a2+a2=22,
解得a=,
所以正方形的边长为,
则正方形ABCD的周长为4.
故选:D.
3.解:∵AC是正方形ABCD的对角线,
∴∠CAB=∠ACB=45°,
∵AC=AE,
∴∠ACE=∠AEC,
∵∠ACE+∠AEC+∠CAE=180°,
∴∠ACE=∠AEC=67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°,
故选:D.
4.解:A、当AB⊥BD时,∠ABD=90°,则∠ABC>90°,当AC⊥BD,四边形ABCD是菱形,故A错误;
B、由四边形ABCD是平行四边形,AC=BD,则四边形ABCD为矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、由四边形ABCD是平行四边形,AB=BC,则四边形ABCD为菱形,故D错误.
故选:C.
5.解:∵∠1=∠A+∠3,∠2=∠A+∠4,
∴∠1+∠2=∠A+∠3+∠4+∠A=180°+90°=270°.
故选:D.
6.解:∵四边形ABCD是正方形,
∴AB=AD,∠ADC=90°,∠DAC=45°,
∵AE=AB,
∴AD=AE,
∴∠ADE=∠AED=67.5°,
∴∠CDE=90°﹣67.5°=22.5°,
故选:B.
7.解:∵四边形CEFG是正方形,
∴∠CEF=90°,
∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣28°﹣90°=62°,
∴∠D=180°﹣∠CED﹣∠ECD=180°﹣62°﹣43°=75°,
∵四边形ABCD为平行四边形,
∴∠B=∠D=75°(平行四边形对角相等).
故选:B.
8.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
9.解:如图所示:作CD⊥x轴于D,作AE⊥x轴于E,
则∠AEO=∠ODC=90°,
∴∠OAE+∠AOE=90°,
∵四边形OABC是正方形,
∴OA=CO=BA,∠AOC=90°,
∴∠AOE+∠COD=90°,
∴∠OAE=∠COD,
在△AOE和△OCD中,
,
∴△AOE≌△OCD(AAS),
∴AE=OD,OE=CD,
∵点A的坐标是(﹣3,1),
∴OE=3,AE=1,
∴OD=1,CD=3,
∴C(1,3),
故选:A.
10.解:如图所示,连接BD交AC于O,则AC⊥BD,
正方形ABCD的面积S1=AC×BD=AC×BO,
AEFC的面积S2=AC×BO,
∴S1=S2,
故选:B.
二.填空题(共8小题,满分32分)
11.解:根据有一组邻边相等或对角线互相垂直的矩形是正方形,得到应该添加的条件为:AB=BC或BC=CD或CD=DA或DA=AB或AC⊥BD.
故答案为:AB=BC.
12.解:∵四边形ABCD为正方形,BC=4,
∴∠CDF=∠BCE=90°,AD=DC=BC=4,
又∵DE=AF=1,
∴CE=DF=3,
∴在△CDF和△BCE中,
,
∴△CDF≌△BCE(SAS),
∴∠DCF=∠CBE,
∵∠DCF+∠BCF=90°,
∴∠CBE+∠BCF=90°,
∴∠BGC=90°,
∵在Rt△BCE中,BC=4,CE=3,
∴BE=5,
∴BE CG=BC CE,
∴CG===,
∵△CDF≌△BCE(SAS),
∴CF=BE=5,
∴GF=CF﹣CG=5﹣=2.6.
故答案为:2.6.
13.解:如右图,连接AE,
∵BD为正方形ABCD的对角线,
∴∠BDC=45°,
∵DE=DC=AD,
∴∠DEC=∠DCE==67.5°,
∵∠DCB=90°,
∴∠BCE=90°﹣∠DCE=90°﹣67.5°=22.5°,
∵EF=EC,
∴∠FEC=180°﹣∠EFC﹣∠ECF=180°﹣22.5°﹣22.5°=135°,
∵∠BEC=180°﹣∠DEC=180°﹣67.5°=112.5°,
∴∠BEF=135°﹣112.5°=22.5°,
∵AD=DE,∠ADE=45°,
∴∠AED==67.5°,
∴∠BEF+∠AED=22.5°+67.5°=90°,
∴∠AEF=180°﹣90°=90°,
在△ADE和△EDC中,
,
∴△ADE≌△EDC(SAS),
∴AE=EC,
∴AE=EF,
即△AEF为等腰直角三角形,
∴∠AFE=45°,
∴∠AFB=∠AFE+∠BFE=45°+22.5°=67.5°,
∵∠ABF=90°,
∴∠BAF=90°﹣∠AFB=90°﹣67.5°=22.5°,
故答案为:22.5°.
14.解:因为有一组邻边相等的矩形是正方形,
故答案为:AB=AD(答案不唯一).
15.解:如图,过点O作OE⊥AD于点E,OF⊥DC于点F,设两个正方形的边的交点分别为点G和点H,如图所示:
则有∠OEG=∠OFD=∠D=90°,
∵O是正方形ABCD的中心,
∴OE=OF,∠EOF=90°,
∴四边形OEDF为正方形.
∵∠GOH=90°,∠EOF=90°,
∴∠EOG=∠FOH,
在△EOG和△FOH中,
,
∴△EOG≌△FOH(ASA).
∴阴影部分的面积等于正方形OEDF的面积,
∵两个边长均为6的正方形重叠在一起,
∴正方形OEDF的面积为:3×3=9.
∴阴影部分的面积为9.
故答案为:9.
16.解:如图,连接AC,
∵四边形ABCD是正方形,
∴AC=BC,∠ACB=45°,
∵CE=BC,
∴AC=CE,
∴∠AEB=∠CAE,
∵∠ACB=∠CAE+∠E=2∠AEB=45°,
∴∠AEB=22.5°.
故答案为22.5°.
17.解:∵正方形ABCD中,∠BAD=∠ADF=90°,∠BAE=56°,
∴∠DAF=34°,∠DFE=56°,
∵AD=CD,∠ADE=∠CDE,DE=DE,
∴△ADE≌△CDE(SAS),
∴∠DCE=∠DAF=34°,
∵∠DFE是△CEF的外角,
∴∠CEF=∠DFE﹣∠DCE=56°﹣34°=22°,
故答案为:22.
18.解:(1)∵正方形ABCD的边长为2,
∴AB=BC=2,∠ABC=90°,
∵M是BC的中点,
∴BM=,
∴,
故答案为:;
(2)过F作FG⊥AB于G,则FG=BC=AB,∠ABM=∠FGE=90°,
∵EF⊥AM,
∴∠BAM+∠AEN=∠AEN+∠GFE=90°,
∴∠BAM=∠GFE,
∴△ABM≌△FGE(SAS),
∴AM=EF,
将EF沿EM方向平移至MH,连接FH,则EF=MH,∠AMH=90°,EM=FH,
当A、F、H三点共线时,EM+AF=FH+AF=AH的值最小,
此时EM+AF=AH=,
∴EM+AF的最小值为,
故答案为:.
三.解答题(共6小题,满分48分)
19.(1)证明:由正方形对角线平分每一组对角可知:∠DAE=∠BCF=45°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)解:∵AB=AD=,
∴BD===8,
由正方形对角线相等且互相垂直平分可得:AC=BD=8,DO=BO=4,OA=OC=4,
又AE=CF=2,
∴OA﹣AE=OC﹣CF,
即OE=OF=4﹣2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE===2.
∴4DE=,
故四边形BEDF的周长为8.
20.证明;(1)∵四边形ABCD是正方形,
∴∠ABC=90°=∠C,AB=BC,
∴∠ABF+∠CBF=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)∵AF=10,AD=8,
∴DF===6,
∴CF=8﹣6=2,
∴BF===2,
∴AE=2.
21.解:(1)如图,取AB的中点M,连接ME,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=∠DCG=90°,
∵点E是边BC的中点,
∴AM=EC=BE,
∴∠BME=∠BEM=45°,
∴∠AME=135°,
∵CF平分∠DCG,
∴∠DCF=∠FCG=45°,
∴∠ECF=180°﹣∠FCG=135°,
∴∠AME=∠ECF,
∵∠AEF=90°,
∴∠AEB+∠CEF=90°,
又∠AEB+∠MAE=90°,
∴∠MAE=∠CEF,
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)∵△AME≌△ECF,
∴S△AME=S△ECF=2,AE=EF,
∴2=×AM×BE,
∴4=BE2,
∴BE=2,
∴AB=4,
∴AE===2,
∴AE=EF=2.
22.(1)证明:在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠BAG+∠DAG=90°,
∵BF⊥AE,DG⊥AE,
∴∠BFA=∠AGD=90°,∠BAG+∠ABF=90°,
∴∠DAG=∠ABF,
∴△ABF≌△DAG(AAS);
(2)∵△ABF≌△DAG,
∴AF=DG=2,
∵FG=1,
∴AG=AF+FG=3,
∴BF=AG=3,
在Rt△ABE中,AB===.
23.解:(1)证明:∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
(2)①成立.
∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
②设正方形ABCD的边长为x,则BC=CD=x,
∴BD==x,
∵正方形CFGM的边长为1,
∴BF=BC+CF=x+1.
∵BD=BF,
∴x=x+1,
∴x=+1.
∴4x=4+4.
∴正方形ABCD的周长为4+4.
24.证明:(1)如图1:把△ABE绕点A逆时针旋转90°至△ADG,
则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BEA=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△EAF中,
,
∴△GAF≌△EAF(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF;
(2)当∠BAD=2∠EAF时,仍有EF=BE+FD,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
一.选择题(共10小题,满分40分)
1.正方形具备而菱形不具备的性质是( )
A.四条边都相等 B.四个角都是直角
C.对角线互相垂直平分 D.每条对角线平分一组对角
2.正方形ABCD的一条对角线长为2,则正方形ABCD的周长为( )
A.4 B.8 C.2 D.4
3.如图,正方形ABCD中,延长AB至E,使AE=AC,连接CE,则∠BCE=( )
A.10° B.20° C.30° D.22.5°
4.已知四边形ABCD是平行四边形,则下列结论中正确的是( )
A.当AB⊥BD时,它是菱形 B.当AC=BD时,它是正方形
C.当∠ABC=90°时,它是矩形 D.当AB=BC时,它是矩形
5.如图,将一个正方形剪去一个角后,∠1+∠2等于( )
A.120° B.170° C.220° D.270°
6.如图,正方形ABCD中,点E是对角线AC上的一点,且AE=AB,连接BE,DE,则∠CDE的度数为( )
A.20° B.22.5° C.25° D.30°
7.如图,有一个平行四边形ABCD和一个正方形CEFG,其中点E在边AD上.若∠ECD=43°,∠AEF=28°,则∠B的度数为( )
A.55° B.75° C.65° D.60°
8.如图,在正方形ABCD中,AB=2,P是AD边上的动点,PE⊥AC于点E,PF⊥BD于点F,则PE+PF的值为( )
A.4 B.2 C. D.2
9.如图,在正方形OABC中,点A的坐标是(﹣3,1),则C点的坐标是( )
A.(1,3) B.(2,3) C.(3,2) D.(3,1)
10.如图,正方形ABCD和 AEFC,点B在EF边上,若正方形ABCD和 AEFC的面积分别是S1、S2的大小关系是( )
A.S1>S2 B.S1=S2 C.S1<S2 D.无法确定
二.填空题(共8小题,满分32分)
11.要使矩形ABCD成为正方形,可添加的条件是 (写一个即可).
12.如图,正方形ABCD中,点E、F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则GF的长为 .
13.如图,BD是正方形ABCD的一条对角线,E是BD上一点,F是CB延长线上一点,连接CE,EF,AF.若DE=DC,EF=EC,则∠BAF的度数为 .
14.如图,四边形ABCD是矩形,则只须补充条件 (用字母表示只添加一个条件)就可以判定四边形ABCD是正方形.
15.如图,两个边长均为6的正方形重叠在一起,O是正方形ABCD的中心,则阴影部分的面积是 .
16.如图,正方形ABCD.延长BC到E,连接AE,若CE=BC,则∠AEB= .
17.如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连接CE.若∠BAE=56°,则∠CEF= °.
18.如图,正方形ABCD的边长为2,M是BC的中点,N是AM上的动点,过点N作EF⊥AM分别交AB,CD于点E,F.
(1)AM的长为 ;
(2)EM+AF的最小值为 .
三.解答题(共6小题)
19.如图,在正方形ABCD中,对角线AC,BD相交于点O,点E,F是对角线AC上的两点,且AE=CF.连接DE,DF,BE,BF.
(1)证明:△ADE≌△CBF.
(2)若AB=4,AE=2,求四边形BEDF的周长.
20.如图,正方形ABCD边长为8,E,F分别是BC,CD上的点,且AE⊥BF.
(1)求证:AE=BF.
(2)若AF=10,求AE的长.
21.如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角∠DCG的平分线CF于点F.
(1)求证:AE=EF;
(2)若S△CEF=2,求EF的长.
22.已知,如图正方形ABCD中,E为CD边上一点,BF⊥AE于点F,DG⊥AE于点G.
(1)求证:△ABF≌△DAG.
(2)若FG=1,DG=2,求AB的长.
23.正方形ABCD中,M为射线CD上一点(不与D重合),以CM为边,在正方形ABCD的异侧作正方形CFGM,连接BM,DF,直线BM与DF交于点E.
(1)如图1,若M在CD的延长线上,求证:DF=BM,DF⊥BM;
(2)如图2,若M移到边CD上.
①在(1)中结论是否仍成立?(直接回答不需证明)
②连接BD,若BD=BF,且正方形CFGM的边长为1,试求正方形ABCD的周长.
24.(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
参考答案
一.选择题(共10小题,满分40分)
1.解:A、正方形和菱形均具有,故不正确;
B、菱形的四个角相等但不一定是直角,故正确;
C、正方形和菱形均具有此性质,故不正确;
D、正方形和菱形均具有此性质,故不正确;
故选:B.
2.解:因为正方形ABCD的一条对角线长为2,
设正方形的边长为a,
根据勾股定理,得a2+a2=22,
解得a=,
所以正方形的边长为,
则正方形ABCD的周长为4.
故选:D.
3.解:∵AC是正方形ABCD的对角线,
∴∠CAB=∠ACB=45°,
∵AC=AE,
∴∠ACE=∠AEC,
∵∠ACE+∠AEC+∠CAE=180°,
∴∠ACE=∠AEC=67.5°,
∴∠BCE=∠ACE﹣∠ACB=67.5°﹣45°=22.5°,
故选:D.
4.解:A、当AB⊥BD时,∠ABD=90°,则∠ABC>90°,当AC⊥BD,四边形ABCD是菱形,故A错误;
B、由四边形ABCD是平行四边形,AC=BD,则四边形ABCD为矩形,故B错误;
C、当∠ABC=90°时,四边形ABCD是矩形,故C正确;
D、由四边形ABCD是平行四边形,AB=BC,则四边形ABCD为菱形,故D错误.
故选:C.
5.解:∵∠1=∠A+∠3,∠2=∠A+∠4,
∴∠1+∠2=∠A+∠3+∠4+∠A=180°+90°=270°.
故选:D.
6.解:∵四边形ABCD是正方形,
∴AB=AD,∠ADC=90°,∠DAC=45°,
∵AE=AB,
∴AD=AE,
∴∠ADE=∠AED=67.5°,
∴∠CDE=90°﹣67.5°=22.5°,
故选:B.
7.解:∵四边形CEFG是正方形,
∴∠CEF=90°,
∵∠CED=180°﹣∠AEF﹣∠CEF=180°﹣28°﹣90°=62°,
∴∠D=180°﹣∠CED﹣∠ECD=180°﹣62°﹣43°=75°,
∵四边形ABCD为平行四边形,
∴∠B=∠D=75°(平行四边形对角相等).
故选:B.
8.解:在正方形ABCD中,OA⊥OB,∠OAD=45°,
∵PE⊥AC,PF⊥BD,
∴四边形OEPF为矩形,△AEP是等腰直角三角形,
∴PF=OE,PE=AE,
∴PE+PF=AE+OE=OA,
∵正方形ABCD的边长为2,
∴OA=AC==.
故选:C.
9.解:如图所示:作CD⊥x轴于D,作AE⊥x轴于E,
则∠AEO=∠ODC=90°,
∴∠OAE+∠AOE=90°,
∵四边形OABC是正方形,
∴OA=CO=BA,∠AOC=90°,
∴∠AOE+∠COD=90°,
∴∠OAE=∠COD,
在△AOE和△OCD中,
,
∴△AOE≌△OCD(AAS),
∴AE=OD,OE=CD,
∵点A的坐标是(﹣3,1),
∴OE=3,AE=1,
∴OD=1,CD=3,
∴C(1,3),
故选:A.
10.解:如图所示,连接BD交AC于O,则AC⊥BD,
正方形ABCD的面积S1=AC×BD=AC×BO,
AEFC的面积S2=AC×BO,
∴S1=S2,
故选:B.
二.填空题(共8小题,满分32分)
11.解:根据有一组邻边相等或对角线互相垂直的矩形是正方形,得到应该添加的条件为:AB=BC或BC=CD或CD=DA或DA=AB或AC⊥BD.
故答案为:AB=BC.
12.解:∵四边形ABCD为正方形,BC=4,
∴∠CDF=∠BCE=90°,AD=DC=BC=4,
又∵DE=AF=1,
∴CE=DF=3,
∴在△CDF和△BCE中,
,
∴△CDF≌△BCE(SAS),
∴∠DCF=∠CBE,
∵∠DCF+∠BCF=90°,
∴∠CBE+∠BCF=90°,
∴∠BGC=90°,
∵在Rt△BCE中,BC=4,CE=3,
∴BE=5,
∴BE CG=BC CE,
∴CG===,
∵△CDF≌△BCE(SAS),
∴CF=BE=5,
∴GF=CF﹣CG=5﹣=2.6.
故答案为:2.6.
13.解:如右图,连接AE,
∵BD为正方形ABCD的对角线,
∴∠BDC=45°,
∵DE=DC=AD,
∴∠DEC=∠DCE==67.5°,
∵∠DCB=90°,
∴∠BCE=90°﹣∠DCE=90°﹣67.5°=22.5°,
∵EF=EC,
∴∠FEC=180°﹣∠EFC﹣∠ECF=180°﹣22.5°﹣22.5°=135°,
∵∠BEC=180°﹣∠DEC=180°﹣67.5°=112.5°,
∴∠BEF=135°﹣112.5°=22.5°,
∵AD=DE,∠ADE=45°,
∴∠AED==67.5°,
∴∠BEF+∠AED=22.5°+67.5°=90°,
∴∠AEF=180°﹣90°=90°,
在△ADE和△EDC中,
,
∴△ADE≌△EDC(SAS),
∴AE=EC,
∴AE=EF,
即△AEF为等腰直角三角形,
∴∠AFE=45°,
∴∠AFB=∠AFE+∠BFE=45°+22.5°=67.5°,
∵∠ABF=90°,
∴∠BAF=90°﹣∠AFB=90°﹣67.5°=22.5°,
故答案为:22.5°.
14.解:因为有一组邻边相等的矩形是正方形,
故答案为:AB=AD(答案不唯一).
15.解:如图,过点O作OE⊥AD于点E,OF⊥DC于点F,设两个正方形的边的交点分别为点G和点H,如图所示:
则有∠OEG=∠OFD=∠D=90°,
∵O是正方形ABCD的中心,
∴OE=OF,∠EOF=90°,
∴四边形OEDF为正方形.
∵∠GOH=90°,∠EOF=90°,
∴∠EOG=∠FOH,
在△EOG和△FOH中,
,
∴△EOG≌△FOH(ASA).
∴阴影部分的面积等于正方形OEDF的面积,
∵两个边长均为6的正方形重叠在一起,
∴正方形OEDF的面积为:3×3=9.
∴阴影部分的面积为9.
故答案为:9.
16.解:如图,连接AC,
∵四边形ABCD是正方形,
∴AC=BC,∠ACB=45°,
∵CE=BC,
∴AC=CE,
∴∠AEB=∠CAE,
∵∠ACB=∠CAE+∠E=2∠AEB=45°,
∴∠AEB=22.5°.
故答案为22.5°.
17.解:∵正方形ABCD中,∠BAD=∠ADF=90°,∠BAE=56°,
∴∠DAF=34°,∠DFE=56°,
∵AD=CD,∠ADE=∠CDE,DE=DE,
∴△ADE≌△CDE(SAS),
∴∠DCE=∠DAF=34°,
∵∠DFE是△CEF的外角,
∴∠CEF=∠DFE﹣∠DCE=56°﹣34°=22°,
故答案为:22.
18.解:(1)∵正方形ABCD的边长为2,
∴AB=BC=2,∠ABC=90°,
∵M是BC的中点,
∴BM=,
∴,
故答案为:;
(2)过F作FG⊥AB于G,则FG=BC=AB,∠ABM=∠FGE=90°,
∵EF⊥AM,
∴∠BAM+∠AEN=∠AEN+∠GFE=90°,
∴∠BAM=∠GFE,
∴△ABM≌△FGE(SAS),
∴AM=EF,
将EF沿EM方向平移至MH,连接FH,则EF=MH,∠AMH=90°,EM=FH,
当A、F、H三点共线时,EM+AF=FH+AF=AH的值最小,
此时EM+AF=AH=,
∴EM+AF的最小值为,
故答案为:.
三.解答题(共6小题,满分48分)
19.(1)证明:由正方形对角线平分每一组对角可知:∠DAE=∠BCF=45°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(SAS).
(2)解:∵AB=AD=,
∴BD===8,
由正方形对角线相等且互相垂直平分可得:AC=BD=8,DO=BO=4,OA=OC=4,
又AE=CF=2,
∴OA﹣AE=OC﹣CF,
即OE=OF=4﹣2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE===2.
∴4DE=,
故四边形BEDF的周长为8.
20.证明;(1)∵四边形ABCD是正方形,
∴∠ABC=90°=∠C,AB=BC,
∴∠ABF+∠CBF=90°,
∵AE⊥BF,
∴∠ABF+∠BAE=90°,
∴∠BAE=∠CBF,
∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)∵AF=10,AD=8,
∴DF===6,
∴CF=8﹣6=2,
∴BF===2,
∴AE=2.
21.解:(1)如图,取AB的中点M,连接ME,
∵四边形ABCD是正方形,
∴AB=BC,∠B=∠BCD=∠DCG=90°,
∵点E是边BC的中点,
∴AM=EC=BE,
∴∠BME=∠BEM=45°,
∴∠AME=135°,
∵CF平分∠DCG,
∴∠DCF=∠FCG=45°,
∴∠ECF=180°﹣∠FCG=135°,
∴∠AME=∠ECF,
∵∠AEF=90°,
∴∠AEB+∠CEF=90°,
又∠AEB+∠MAE=90°,
∴∠MAE=∠CEF,
∴△AME≌△ECF(ASA),
∴AE=EF;
(2)∵△AME≌△ECF,
∴S△AME=S△ECF=2,AE=EF,
∴2=×AM×BE,
∴4=BE2,
∴BE=2,
∴AB=4,
∴AE===2,
∴AE=EF=2.
22.(1)证明:在正方形ABCD中,AB=AD,∠BAD=90°,
∴∠BAG+∠DAG=90°,
∵BF⊥AE,DG⊥AE,
∴∠BFA=∠AGD=90°,∠BAG+∠ABF=90°,
∴∠DAG=∠ABF,
∴△ABF≌△DAG(AAS);
(2)∵△ABF≌△DAG,
∴AF=DG=2,
∵FG=1,
∴AG=AF+FG=3,
∴BF=AG=3,
在Rt△ABE中,AB===.
23.解:(1)证明:∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
(2)①成立.
∵四边形ABCD与四边形CFGM都是正方形,
∴∠BCM=∠FCD=90°,BC=CD,CM=CF.
在△BCM和△DCF中,
,
∴△BCM≌△DCF(SAS).
∴DF=BM,∠CFD=∠CMB.
∵∠BMC+∠CBM=90°,
∴∠CBM+∠CFD=90°,
∴∠BEF=90°,
∴DF⊥BM;
②设正方形ABCD的边长为x,则BC=CD=x,
∴BD==x,
∵正方形CFGM的边长为1,
∴BF=BC+CF=x+1.
∵BD=BF,
∴x=x+1,
∴x=+1.
∴4x=4+4.
∴正方形ABCD的周长为4+4.
24.证明:(1)如图1:把△ABE绕点A逆时针旋转90°至△ADG,
则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BEA=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△EAF中,
,
∴△GAF≌△EAF(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF;
(2)当∠BAD=2∠EAF时,仍有EF=BE+FD,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
