2022年湘教版数学八年级下册2.6.2 菱形的判定 课时练习(Word版含答案)
文档属性
| 名称 | 2022年湘教版数学八年级下册2.6.2 菱形的判定 课时练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 144.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 00:00:00 | ||
图片预览



文档简介
2022年湘教版数学八年级下册
2.6.2《菱形的判定》课时练习
一、选择题
1.已知 ABCD,给出下列条件:①AC=BD;②∠BAD=90°;③AB=BC;④AC⊥BD,添加其中之一能使 ABCD成为菱形的条件是( )
A.①③ B.②③ C.③④ D.①②③
2.若顺次连接四边形各边中点所得的四边形是菱形,则该四边形一定是( )
A.矩形
B.一组对边相等,另一组对边平行的四边形
C.对角线相等的四边形
D.对角线互相垂直的四边形
3.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A. B. C. D.
4.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
5.如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①②③
6.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.对角线互相垂直的四边形 D.对角线相等的四边形
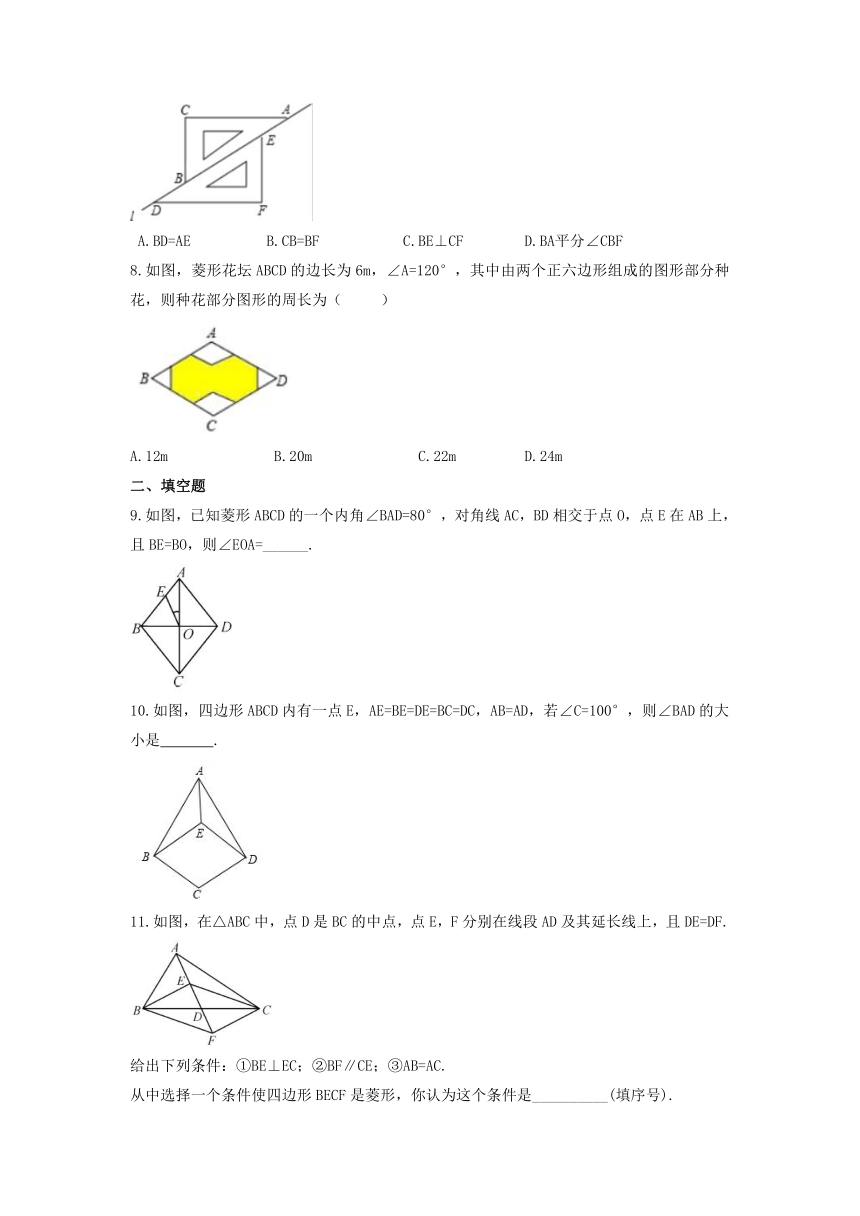
7.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
A.BD=AE B.CB=BF C.BE⊥CF D.BA平分∠CBF
8.如图,菱形花坛ABCD的边长为6m,∠A=120°,其中由两个正六边形组成的图形部分种花,则种花部分图形的周长为( )
A.12m B.20m C.22m D.24m
二、填空题
9.如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=______.
10.如图,四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD,若∠C=100°,则∠BAD的大小是 .
11.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.
给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.
从中选择一个条件使四边形BECF是菱形,你认为这个条件是__________(填序号).
12.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD.
则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.
其中正确的是 (只填写序号)
13.如图,在给定的一张平行四边形纸片上做一个菱形,甲、乙两人的作法如下:
甲:连接AC,做AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断正确的是 .
14.如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
三、解答题
15.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
16.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
17.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于点F,交BC于点E,过点E作EG⊥AB于G,连结GF.求证:四边形CFGE是菱形.
18.如图,已知四边形ABCD为矩形,AD=20cm、AB=10cm.M点从D到A,P点从B到C,两点的速度都为2cm/s;N点从A到B,Q点从C到D,两点的速度都为1cm/s.若四个点同时出发.
(1)判断四边形MNPQ的形状.
(2)四边形MNPQ能为菱形吗?若能,请求出此时运动的时间;若不能,说明理由.
参考答案
1.C
2.C;
3.C.
4.C.
5.A
6.C.
7.A
8.C
9.答案为:65.
10.答案为:50°
11.答案为:菱形.
12.答案为:①②③④.
13.答案为:C.
14.答案为:8.
15.解:(1)∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∵AE∥BF,
∴∠DAB+∠CBA,=180°,
∴∠BAC+∠ABD=(∠DAB+∠ABC)=×180°=90°,
∴∠AOD=90°;
(2)证明:∵AE∥BF,
∴∠ADB=∠DBC,∠DAC=∠BCA,
∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∴∠BAC=∠ACB,∠ABD=∠ADB,
∴AB=BC,AB=AD
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形.
16.(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD=AB=BD=AD,
∴平行四边形ADCE是菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=3.
17.证明:由∠ACB=90°,AE平分∠BAC,EG⊥AB,
易证△ACE≌△AGE,
∴CE=EG,∠AEC=∠AEG.
∵CD是AB边上的高,EG⊥AB,
∴EG∥CD,
∴∠EFC=∠AEG,
∴∠EFC=∠AEC,
∴FC=EC,∴FC=EG,
∴四边形CFGE是平行四边形.
又∵GE=CE,∴四边形CFGE是菱形.
18.解:(1)四边形MNPQ是平行四边形. 理由如下:
在矩形ABCD中,AD=BC=20cm,AB=CD=10cm,且∠A=∠B=∠C=∠D=90°.
设运动时间为t秒,则AN=CQ=t cm,BP=DM=2t cm.
∴BN=DQ=(10﹣t)cm,CP=AM=(20﹣2t)cm.
由勾股定理可得,NP=,MQ=
∴NP=MQ.
同理,可得MN=PQ.
∴四边形MNPQ是平行四边形.
(2)能.理由如下:
∵当四边形MNPQ能为菱形时,NP=QP,
∴=,
∴=,
解得 t=5.
即四边形MNPQ能为菱形时,运动时间是5 s.
2.6.2《菱形的判定》课时练习
一、选择题
1.已知 ABCD,给出下列条件:①AC=BD;②∠BAD=90°;③AB=BC;④AC⊥BD,添加其中之一能使 ABCD成为菱形的条件是( )
A.①③ B.②③ C.③④ D.①②③
2.若顺次连接四边形各边中点所得的四边形是菱形,则该四边形一定是( )
A.矩形
B.一组对边相等,另一组对边平行的四边形
C.对角线相等的四边形
D.对角线互相垂直的四边形
3.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )
A. B. C. D.
4.如图,四边形ABCD的两条对角线相交于点O,且互相平分.添加下列条件,仍不能判定四边形ABCD为菱形的是( )
A.AC⊥BD B.AB=AD C.AC=BD D.∠ABD=∠CBD
5.如图,下列条件之一能使平行四边形ABCD是菱形的为( )
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.
A.①③ B.②③ C.③④ D.①②③
6.若顺次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.对角线互相垂直的四边形 D.对角线相等的四边形
7.如图,两个完全相同的三角尺ABC和DEF在直线l上滑动,可以添加一个条件,使四边形CBFE为菱形,下列选项中错误的是( )
A.BD=AE B.CB=BF C.BE⊥CF D.BA平分∠CBF
8.如图,菱形花坛ABCD的边长为6m,∠A=120°,其中由两个正六边形组成的图形部分种花,则种花部分图形的周长为( )
A.12m B.20m C.22m D.24m
二、填空题
9.如图,已知菱形ABCD的一个内角∠BAD=80°,对角线AC,BD相交于点O,点E在AB上,且BE=BO,则∠EOA=______.
10.如图,四边形ABCD内有一点E,AE=BE=DE=BC=DC,AB=AD,若∠C=100°,则∠BAD的大小是 .
11.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.
给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC.
从中选择一个条件使四边形BECF是菱形,你认为这个条件是__________(填序号).
12.如图,四边形ABCD是轴对称图形,且直线AC是对称轴,AB∥CD.
则下列结论:①AC⊥BD;②AD∥BC;③四边形ABCD是菱形;④△ABD≌△CDB.
其中正确的是 (只填写序号)
13.如图,在给定的一张平行四边形纸片上做一个菱形,甲、乙两人的作法如下:
甲:连接AC,做AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断正确的是 .
14.如图,在□ABCD中,用直尺和圆规作∠BAD的平分线AG,若AD=5,DE=6,则AG的长是 .
三、解答题
15.如图,AE∥BF,AC平分∠BAE,且交BF于点C,BD平分∠ABF,且交AE于点D,AC与BD相交于点O,连接CD
(1)求∠AOD的度数;
(2)求证:四边形ABCD是菱形.
16.如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,且AE∥CD,CE∥AB.
(1)证明:四边形ADCE是菱形;
(2)若∠B=60°,BC=6,求菱形ADCE的高.(计算结果保留根号)
17.如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于点F,交BC于点E,过点E作EG⊥AB于G,连结GF.求证:四边形CFGE是菱形.
18.如图,已知四边形ABCD为矩形,AD=20cm、AB=10cm.M点从D到A,P点从B到C,两点的速度都为2cm/s;N点从A到B,Q点从C到D,两点的速度都为1cm/s.若四个点同时出发.
(1)判断四边形MNPQ的形状.
(2)四边形MNPQ能为菱形吗?若能,请求出此时运动的时间;若不能,说明理由.
参考答案
1.C
2.C;
3.C.
4.C.
5.A
6.C.
7.A
8.C
9.答案为:65.
10.答案为:50°
11.答案为:菱形.
12.答案为:①②③④.
13.答案为:C.
14.答案为:8.
15.解:(1)∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∵AE∥BF,
∴∠DAB+∠CBA,=180°,
∴∠BAC+∠ABD=(∠DAB+∠ABC)=×180°=90°,
∴∠AOD=90°;
(2)证明:∵AE∥BF,
∴∠ADB=∠DBC,∠DAC=∠BCA,
∵AC、BD分别是∠BAD、∠ABC的平分线,
∴∠DAC=∠BAC,∠ABD=∠DBC,
∴∠BAC=∠ACB,∠ABD=∠ADB,
∴AB=BC,AB=AD
∴AD=BC,
∵AD∥BC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴四边形ABCD是菱形.
16.(1)证明:∵AE∥CD,CE∥AB,
∴四边形ADCE是平行四边形,
又∵∠ACB=90°,D是AB的中点,
∴CD=AB=BD=AD,
∴平行四边形ADCE是菱形;
(2)解:过点D作DF⊥CE,垂足为点F,如图所示:
DF即为菱形ADCE的高,
∵∠B=60°,CD=BD,
∴△BCD是等边三角形,
∴∠BDC=∠BCD=60°,CD=BC=6,
∵CE∥AB,
∴∠DCE=∠BDC=60°,
又∵CD=BC=6,
∴在Rt△CDF中,DF=3.
17.证明:由∠ACB=90°,AE平分∠BAC,EG⊥AB,
易证△ACE≌△AGE,
∴CE=EG,∠AEC=∠AEG.
∵CD是AB边上的高,EG⊥AB,
∴EG∥CD,
∴∠EFC=∠AEG,
∴∠EFC=∠AEC,
∴FC=EC,∴FC=EG,
∴四边形CFGE是平行四边形.
又∵GE=CE,∴四边形CFGE是菱形.
18.解:(1)四边形MNPQ是平行四边形. 理由如下:
在矩形ABCD中,AD=BC=20cm,AB=CD=10cm,且∠A=∠B=∠C=∠D=90°.
设运动时间为t秒,则AN=CQ=t cm,BP=DM=2t cm.
∴BN=DQ=(10﹣t)cm,CP=AM=(20﹣2t)cm.
由勾股定理可得,NP=,MQ=
∴NP=MQ.
同理,可得MN=PQ.
∴四边形MNPQ是平行四边形.
(2)能.理由如下:
∵当四边形MNPQ能为菱形时,NP=QP,
∴=,
∴=,
解得 t=5.
即四边形MNPQ能为菱形时,运动时间是5 s.
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
