2021-2022学年苏科版八年级下册7.4频数分布表和频数分布直方图 同步练习(word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级下册7.4频数分布表和频数分布直方图 同步练习(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 330.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 08:49:47 | ||
图片预览



文档简介
7.4 频数分布表和频数分布直方图
一、单选题
1.下列有关频数分布表和频数分布直方图的理解,正确的是( )
A. 频数分布表能清楚地反映事物的变化情况 B. 频数分布直方图能清楚地反映事物的变化情况
C. 频数分布直方图能清楚地表示出各部分在总体中所占的百分比 D. 二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目
2、绘制频数直方图时,计算出最大值与最小值的差为25 cm,若取组距为4 cm,则最好分( )
A.4组 B.5组 C.6组 D.7组
3、如图所示是某班60名学生一分钟跳绳测试成绩的频数直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么一分钟跳绳次数在100次以上的学生有( )
A.12人 B.20人 C.25人 D.30人
4、已知样本有30个数据,在样本的频数直方图中各小长方形的高的比依次为2∶4∶3∶1,
则第二小组的频数为( )
A.4 B.12 C.9 D.8
5.为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图 请根据图形计算,跳绳次数 在 范围内人数占抽查学生总人数的百分比为
A. B. C. D.
6为了了解本校八年级学生的体能情况,随机抽查了其中名学生,测试了分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,则仰卧起坐次数在次含次以上的人数共有
A. 人 B. 人 C. 人 D. 都不对
7在样本的频数分布直方图中,有个小长方形若中间个小长方形的面积等于其他个小长方形面积之和的四分之一,且样本数据有个,则中间一组的频数为
A. B. C. D.
8为了绘制一批数据的频率分布直方图,首先要算出这批数据的变化范围,数据的变化范围是指数据的
A. 最大值 B. 最小值
C. 最大值与最小值的差 D. 个数
9.小聪对他所在小区居民每天微信阅读时间进行了抽样调查,并绘制成了如图所示的统计图.根据图中信息,其中正确的是( )
①小聪一共抽样调查了60人
②每天微信阅读时间多于50分钟的人数有12人
③每天微信阅读时间30~40分钟的人数最多
④每天微信阅读时间不足30分钟的人数多于调查总人数的一半
A. ①② B. ②③ C. ②④ D. ③④
10.小明统计了同学们5月份平均每天观看北京市“空中课堂”的时间,并绘制了统计图,如图所示下面有四个推断
①此次调查中,小明一共调查了100名学生
②此次调查中,平均每天观看时间不足30分钟的人数占总人数的10%
③此次调查中,平均每天观看时间超过60分钟的人数超过调查总人数的一半
④此次调查中,平均每天观看时间不足60分钟的人数少于平均每天观看时间在60-90分钟的人数
所有合理推断的序号是( )
A. ①② B. ①④ C. ③④ D. ②③④
二、填空题
11、有一个含有50个数据的数据组,已知最小数据是15,最大数据是45,且各数据都是整数,则这50个数据分为8组时,组距是________;若第1组的下限为14.5,则其上限为________,最末一组的上限为________.
12、阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调査结果绘制了如下不完整的统计表.则表中的a=____.
组别 时间/时 频数(人) 频率
A 0≤t≤0.5 6 0.15
B 0.5≤t≤1 a 0.3
13、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40% 25% m
则表格中m的值为
14、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
15、空气质量指数,简称AQI,如果AQI在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最近一段时间的AQI画出的频数分布直方图如图所示.已知每天的AQI都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 %.
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
17、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
18、某校七年级(1)班为了了解同学们一天零花钱的消费情况,对本班同学开展了调查,将同学一周的零花钱以2元为组距,绘制如图的频数直方图,已知从左到右各组的频数之比为2∶3∶4∶2∶1.
(1)若该班有48人,则零花钱用得最多的是第 组,有 人;
(2)零花钱在8元以上的共有 人.
三、解答题
19.第一次模拟考试后,数学科陈老师把一班的数学成绩制成如图的统计图(图中每组数据包含横轴上左边的数据不含右边的数据),并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8.
请结合统计图完成下列问题:
(1)这个班学生是多少人?
(2)成绩不少于90分为优秀,那么这个班成绩的优秀率是多少?
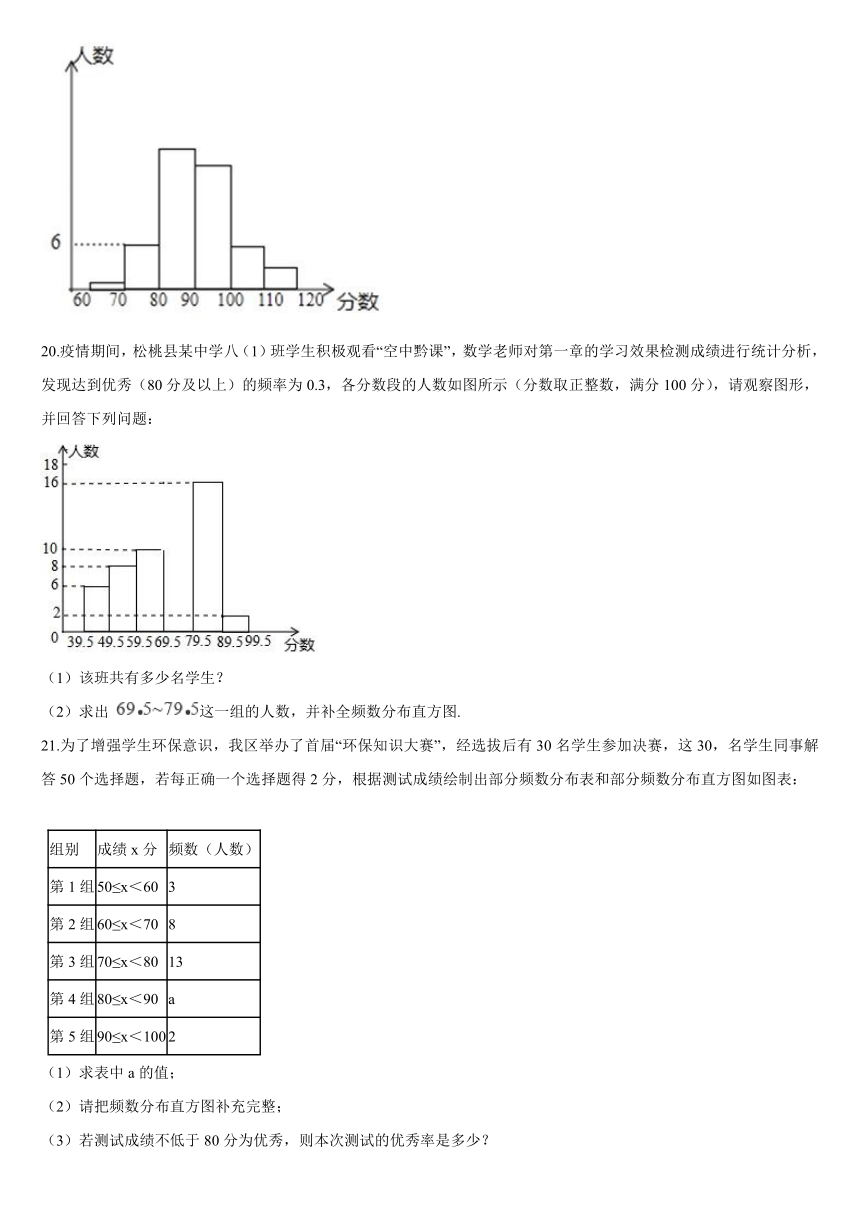
20.疫情期间,松桃县某中学八(1)班学生积极观看“空中黔课”,数学老师对第一章的学习效果检测成绩进行统计分析,发现达到优秀(80分及以上)的频率为0.3,各分数段的人数如图所示(分数取正整数,满分100分),请观察图形,并回答下列问题:
(1)该班共有多少名学生?
(2)求出 这一组的人数,并补全频数分布直方图.
21.为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 成绩x分 频数(人数)
第1组 50≤x<60 3
第2组 60≤x<70 8
第3组 70≤x<80 13
第4组 80≤x<90 a
第5组 90≤x<100 2
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(4)第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导,则第4组的小宇与小强能同时抽到的概率是多少?
22、在开展“经典阅读”活动中,某校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计图表.
根据图表信息回答下列问题:
(1)填空:a=____,b=____,m=____,n=____.
(2)将频数直方图补充完整.
(3)若该校有3000名学生,请根据上述调查结果,估计该校学生一周的课外阅读时间不足3 h的人数.
23、为了让地震受灾的儿童得到救助,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区共有1000户住户参与捐款,
请根据以上信息估计,全社区捐款不少于300元的户数是 户.
24、为了了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘制成如图所示的频数直方图,已知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为____.
(2)绘制扇形统计图时,成绩x在“70≤x<80”范围内所对应扇形的圆心角的度数为____.
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,
则获得“优秀”的学生大约有____人.
25.垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法为了增强同学们垃圾分类的意识,某校举行一场学生在线参与垃圾分类处理知识测试(满分100分,得分均为整数).学校从全校1200名学生中随机抽取部分学生的成绩,绘制成如下不完整的统计图表.抽取的部分学生测试成绩的频数分布表
成绩 (分) 频数(人) 百分比
10
15
40
15
由图表中给出的信息回答下列问题:
(1)随机抽取的学生总人数为________, ________, ________.
(2)补全频数分布直方图.
(3)如果成绩在80分以上(包括80分)为优秀,求成绩为优秀的人数占被抽取人数的百分比.
参考答案
一、单选题
1-10 DDDBC CBCBC
二、填空题
11、有一个含有50个数据的数据组,已知最小数据是15,最大数据是45,且各数据都是整数,则这50个数据分为8组时,组距是________;若第1组的下限为14.5,则其上限为________,最末一组的上限为________.
[解析] 45-15=30,3<30÷8<4,∴组距应为4.若第1组的下限为14.5,则其上限为14.5+4=18.5;最末一组的上限为14.5+4×8=14.5+32=46.5.
[答案] 4 18.5 46.5
12、阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调査结果绘制了如下不完整的统计表.则表中的a=____.
组别 时间/时 频数(人) 频率
A 0≤t≤0.5 6 0.15
B 0.5≤t≤1 a 0.3
【解析】 ∵被调查的总人数为6÷0.15=40(人),
∴B组的人数为40×0.3=12(人),即a=12.
13、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40% 25% m
则表格中m的值为 10%
14、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= 9 .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
15、空气质量指数,简称AQI,如果AQI在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最近一段时间的AQI画出的频数分布直方图如图所示.已知每天的AQI都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 %.
【解答】解:空气质量类别为优和良的天数占总天数的百分比为×100%=80%,
故答案为:80.
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
【解答】解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是=0.4.
故答案为:0.4.
17、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= 9 .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
18、某校七年级(1)班为了了解同学们一天零花钱的消费情况,对本班同学开展了调查,将同学一周的零花钱以2元为组距,绘制如图的频数直方图,已知从左到右各组的频数之比为2∶3∶4∶2∶1.
(1)若该班有48人,则零花钱用得最多的是第3 组,有16 人;
(2)零花钱在8元以上的共有12 人.
三、解答题
19.【答案】 解:(1)这个班学生数是:6÷(0.14﹣0.02)=50(人);
(2)第三组的频率是:(0.14﹣0.02)×=0.36,
则这个班的优秀率是:1﹣0.14﹣0.36=0.50=50%.
20.【答案】 (1)解:由题意可得: (人)
答:该班共有学生 人;
(2)解:由题意可知, 这一组的人数为:
(人)
补全频数分布直方图如图:
21.【答案】 解:(1)表中a的值是:a=30﹣3﹣8﹣13﹣2=4;(2)根据题意画图如下:(3)本次测试的优秀率是=0.20=20%.答:本次测试的优秀率是20%;(4)用A表示小宇,B表示小强,C、D表示其他两名同学,根据题意画树状图如下:共有24种情况,小宇与小强能同时抽到的情况有12种,则小宇与小强能同时抽到的概率为=.
22、在开展“经典阅读”活动中,某校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计图表.
根据图表信息回答下列问题:
(1)填空:a=____,b=____,m=____,n=____.
(2)将频数直方图补充完整.
(3)若该校有3000名学生,请根据上述调查结果,估计该校学生一周的课外阅读时间不足3 h的人数.
【解】 (1)∵b=18÷0.12=150,∴n=36÷150=0.24,
∴m=1-0.12-0.3-0.24-0.14=0.2,
∴a=0.2×150=30.
(2)补全频数直方图如解图中斜纹所示.
(3)3000×(0.12+0.2)=960.
答:估计该校学生一周的课外阅读时间不足3 h的人数为960.
23、为了让地震受灾的儿童得到救助,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区共有1000户住户参与捐款,
请根据以上信息估计,全社区捐款不少于300元的户数是 户.
解:(1)B组捐款户数是10,则A组捐款户数为10×=2,
样本容量为(2+10)÷(1﹣8%﹣40%﹣28%)=50.
(2)统计表C、D、E 组的户数分别为20,14,4.
组别 捐款额(x)元 户数
A 1≤x<50 a
B 100≤x<200 10
C 200≤x<300 20
D 300≤x<400 14
E x≥400 4
(3)估计全社区捐款不少于300元的户数是1000×(28%+8%)=360(户).
24、为了了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘制成如图所示的频数直方图,已知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为____.
(2)绘制扇形统计图时,成绩x在“70≤x<80”范围内所对应扇形的圆心角的度数为____.
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,
则获得“优秀”的学生大约有____人.
【解】 (1)a=30-(2+12+8+2)=6,故a=6.
(2)成绩x在“70≤x<80”范围内所对应扇形的圆心角的度数为360°×=144°.
(3)获得“优秀”的学生大约有300×=100(人).
25.【答案】 (1)100;20;15%
(2)解:补全图形如下:
(3)解:成绩优秀的人数占被抽取人数的百分比为
解:(1)∵成绩在80≤a<90的频数为40,百分比为40%,
∴ 抽取的学生总人数为40÷40%=100名,
∴m=100×20%=20,n=15÷100=15%.
故答案为:100;20;15%;
一、单选题
1.下列有关频数分布表和频数分布直方图的理解,正确的是( )
A. 频数分布表能清楚地反映事物的变化情况 B. 频数分布直方图能清楚地反映事物的变化情况
C. 频数分布直方图能清楚地表示出各部分在总体中所占的百分比 D. 二者均不能清楚地反映变化情况和在总体中所占的百分比,但能反映出每个项目的具体数目
2、绘制频数直方图时,计算出最大值与最小值的差为25 cm,若取组距为4 cm,则最好分( )
A.4组 B.5组 C.6组 D.7组
3、如图所示是某班60名学生一分钟跳绳测试成绩的频数直方图,从左起第一、二、三、四个小长方形的高的比为1∶4∶3∶2,那么一分钟跳绳次数在100次以上的学生有( )
A.12人 B.20人 C.25人 D.30人
4、已知样本有30个数据,在样本的频数直方图中各小长方形的高的比依次为2∶4∶3∶1,
则第二小组的频数为( )
A.4 B.12 C.9 D.8
5.为了了解某校七年级学生的体能情况,随机调查了其中100名学生,测试学生在1分钟内跳绳的次数,并绘制成如图所示的频数分布直方图 请根据图形计算,跳绳次数 在 范围内人数占抽查学生总人数的百分比为
A. B. C. D.
6为了了解本校八年级学生的体能情况,随机抽查了其中名学生,测试了分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图,则仰卧起坐次数在次含次以上的人数共有
A. 人 B. 人 C. 人 D. 都不对
7在样本的频数分布直方图中,有个小长方形若中间个小长方形的面积等于其他个小长方形面积之和的四分之一,且样本数据有个,则中间一组的频数为
A. B. C. D.
8为了绘制一批数据的频率分布直方图,首先要算出这批数据的变化范围,数据的变化范围是指数据的
A. 最大值 B. 最小值
C. 最大值与最小值的差 D. 个数
9.小聪对他所在小区居民每天微信阅读时间进行了抽样调查,并绘制成了如图所示的统计图.根据图中信息,其中正确的是( )
①小聪一共抽样调查了60人
②每天微信阅读时间多于50分钟的人数有12人
③每天微信阅读时间30~40分钟的人数最多
④每天微信阅读时间不足30分钟的人数多于调查总人数的一半
A. ①② B. ②③ C. ②④ D. ③④
10.小明统计了同学们5月份平均每天观看北京市“空中课堂”的时间,并绘制了统计图,如图所示下面有四个推断
①此次调查中,小明一共调查了100名学生
②此次调查中,平均每天观看时间不足30分钟的人数占总人数的10%
③此次调查中,平均每天观看时间超过60分钟的人数超过调查总人数的一半
④此次调查中,平均每天观看时间不足60分钟的人数少于平均每天观看时间在60-90分钟的人数
所有合理推断的序号是( )
A. ①② B. ①④ C. ③④ D. ②③④
二、填空题
11、有一个含有50个数据的数据组,已知最小数据是15,最大数据是45,且各数据都是整数,则这50个数据分为8组时,组距是________;若第1组的下限为14.5,则其上限为________,最末一组的上限为________.
12、阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调査结果绘制了如下不完整的统计表.则表中的a=____.
组别 时间/时 频数(人) 频率
A 0≤t≤0.5 6 0.15
B 0.5≤t≤1 a 0.3
13、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40% 25% m
则表格中m的值为
14、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
15、空气质量指数,简称AQI,如果AQI在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最近一段时间的AQI画出的频数分布直方图如图所示.已知每天的AQI都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 %.
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
17、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
18、某校七年级(1)班为了了解同学们一天零花钱的消费情况,对本班同学开展了调查,将同学一周的零花钱以2元为组距,绘制如图的频数直方图,已知从左到右各组的频数之比为2∶3∶4∶2∶1.
(1)若该班有48人,则零花钱用得最多的是第 组,有 人;
(2)零花钱在8元以上的共有 人.
三、解答题
19.第一次模拟考试后,数学科陈老师把一班的数学成绩制成如图的统计图(图中每组数据包含横轴上左边的数据不含右边的数据),并给了几个信息:①前两组的频率和是0.14;②第一组的频率是0.02;③自左到右第二、三、四组的频数比为3:9:8.
请结合统计图完成下列问题:
(1)这个班学生是多少人?
(2)成绩不少于90分为优秀,那么这个班成绩的优秀率是多少?
20.疫情期间,松桃县某中学八(1)班学生积极观看“空中黔课”,数学老师对第一章的学习效果检测成绩进行统计分析,发现达到优秀(80分及以上)的频率为0.3,各分数段的人数如图所示(分数取正整数,满分100分),请观察图形,并回答下列问题:
(1)该班共有多少名学生?
(2)求出 这一组的人数,并补全频数分布直方图.
21.为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 成绩x分 频数(人数)
第1组 50≤x<60 3
第2组 60≤x<70 8
第3组 70≤x<80 13
第4组 80≤x<90 a
第5组 90≤x<100 2
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
(4)第4组的同学将抽出3名对第一组3名同学进行“一帮一”辅导,则第4组的小宇与小强能同时抽到的概率是多少?
22、在开展“经典阅读”活动中,某校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计图表.
根据图表信息回答下列问题:
(1)填空:a=____,b=____,m=____,n=____.
(2)将频数直方图补充完整.
(3)若该校有3000名学生,请根据上述调查结果,估计该校学生一周的课外阅读时间不足3 h的人数.
23、为了让地震受灾的儿童得到救助,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区共有1000户住户参与捐款,
请根据以上信息估计,全社区捐款不少于300元的户数是 户.
24、为了了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘制成如图所示的频数直方图,已知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为____.
(2)绘制扇形统计图时,成绩x在“70≤x<80”范围内所对应扇形的圆心角的度数为____.
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,
则获得“优秀”的学生大约有____人.
25.垃圾分类是对垃圾传统收集处理方式的改变,是对垃圾进行有效处理的一种科学管理方法为了增强同学们垃圾分类的意识,某校举行一场学生在线参与垃圾分类处理知识测试(满分100分,得分均为整数).学校从全校1200名学生中随机抽取部分学生的成绩,绘制成如下不完整的统计图表.抽取的部分学生测试成绩的频数分布表
成绩 (分) 频数(人) 百分比
10
15
40
15
由图表中给出的信息回答下列问题:
(1)随机抽取的学生总人数为________, ________, ________.
(2)补全频数分布直方图.
(3)如果成绩在80分以上(包括80分)为优秀,求成绩为优秀的人数占被抽取人数的百分比.
参考答案
一、单选题
1-10 DDDBC CBCBC
二、填空题
11、有一个含有50个数据的数据组,已知最小数据是15,最大数据是45,且各数据都是整数,则这50个数据分为8组时,组距是________;若第1组的下限为14.5,则其上限为________,最末一组的上限为________.
[解析] 45-15=30,3<30÷8<4,∴组距应为4.若第1组的下限为14.5,则其上限为14.5+4=18.5;最末一组的上限为14.5+4×8=14.5+32=46.5.
[答案] 4 18.5 46.5
12、阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取若干名学生进行调查,并依据调査结果绘制了如下不完整的统计表.则表中的a=____.
组别 时间/时 频数(人) 频率
A 0≤t≤0.5 6 0.15
B 0.5≤t≤1 a 0.3
【解析】 ∵被调查的总人数为6÷0.15=40(人),
∴B组的人数为40×0.3=12(人),即a=12.
13、某中学抽取部分学生对“你最喜欢的球类运动”调查问卷,收集整理数据后列频数分布表(部分)如下:
项目 乒乓球 羽毛球 篮球 足球
频数 80 50
百分比 40% 25% m
则表格中m的值为 10%
14、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= 9 .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
15、空气质量指数,简称AQI,如果AQI在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最近一段时间的AQI画出的频数分布直方图如图所示.已知每天的AQI都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 %.
【解答】解:空气质量类别为优和良的天数占总天数的百分比为×100%=80%,
故答案为:80.
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
【解答】解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是=0.4.
故答案为:0.4.
17、某校在践行“社会主义核心价值观”演讲比赛中,对名列前20名的选手的综合分数m进行分组统计,结果如表所示,则a= 9 .
组号 分组 频数
一 6≤m<7 2
二 7≤m<8 7
三 8≤m<9 a
四 9≤m≤10 2
18、某校七年级(1)班为了了解同学们一天零花钱的消费情况,对本班同学开展了调查,将同学一周的零花钱以2元为组距,绘制如图的频数直方图,已知从左到右各组的频数之比为2∶3∶4∶2∶1.
(1)若该班有48人,则零花钱用得最多的是第3 组,有16 人;
(2)零花钱在8元以上的共有12 人.
三、解答题
19.【答案】 解:(1)这个班学生数是:6÷(0.14﹣0.02)=50(人);
(2)第三组的频率是:(0.14﹣0.02)×=0.36,
则这个班的优秀率是:1﹣0.14﹣0.36=0.50=50%.
20.【答案】 (1)解:由题意可得: (人)
答:该班共有学生 人;
(2)解:由题意可知, 这一组的人数为:
(人)
补全频数分布直方图如图:
21.【答案】 解:(1)表中a的值是:a=30﹣3﹣8﹣13﹣2=4;(2)根据题意画图如下:(3)本次测试的优秀率是=0.20=20%.答:本次测试的优秀率是20%;(4)用A表示小宇,B表示小强,C、D表示其他两名同学,根据题意画树状图如下:共有24种情况,小宇与小强能同时抽到的情况有12种,则小宇与小强能同时抽到的概率为=.
22、在开展“经典阅读”活动中,某校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计图表.
根据图表信息回答下列问题:
(1)填空:a=____,b=____,m=____,n=____.
(2)将频数直方图补充完整.
(3)若该校有3000名学生,请根据上述调查结果,估计该校学生一周的课外阅读时间不足3 h的人数.
【解】 (1)∵b=18÷0.12=150,∴n=36÷150=0.24,
∴m=1-0.12-0.3-0.24-0.14=0.2,
∴a=0.2×150=30.
(2)补全频数直方图如解图中斜纹所示.
(3)3000×(0.12+0.2)=960.
答:估计该校学生一周的课外阅读时间不足3 h的人数为960.
23、为了让地震受灾的儿童得到救助,某社区组织“献爱心手拉手”捐款活动,对社区部分捐款户数进行调查和分组统计后,将数据整理成如图所示的统计表和统计图(图中信息不完整).已知A、B两组捐款户数的比为1:5.
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)补全“捐款户数分组统计表和捐款户数统计图1”;
(3)若该社区共有1000户住户参与捐款,
请根据以上信息估计,全社区捐款不少于300元的户数是 户.
解:(1)B组捐款户数是10,则A组捐款户数为10×=2,
样本容量为(2+10)÷(1﹣8%﹣40%﹣28%)=50.
(2)统计表C、D、E 组的户数分别为20,14,4.
组别 捐款额(x)元 户数
A 1≤x<50 a
B 100≤x<200 10
C 200≤x<300 20
D 300≤x<400 14
E x≥400 4
(3)估计全社区捐款不少于300元的户数是1000×(28%+8%)=360(户).
24、为了了解某次“小学生书法比赛”的成绩情况,随机抽取了30名学生的成绩进行统计,并将统计情况绘制成如图所示的频数直方图,已知成绩x(单位:分)均满足“50≤x<100”.根据图中信息回答下列问题:
(1)图中a的值为____.
(2)绘制扇形统计图时,成绩x在“70≤x<80”范围内所对应扇形的圆心角的度数为____.
(3)此次比赛共有300名学生参加,若将“x≥80”的成绩记为“优秀”,
则获得“优秀”的学生大约有____人.
【解】 (1)a=30-(2+12+8+2)=6,故a=6.
(2)成绩x在“70≤x<80”范围内所对应扇形的圆心角的度数为360°×=144°.
(3)获得“优秀”的学生大约有300×=100(人).
25.【答案】 (1)100;20;15%
(2)解:补全图形如下:
(3)解:成绩优秀的人数占被抽取人数的百分比为
解:(1)∵成绩在80≤a<90的频数为40,百分比为40%,
∴ 抽取的学生总人数为40÷40%=100名,
∴m=100×20%=20,n=15÷100=15%.
故答案为:100;20;15%;
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
