10.4 中心对称-课堂练习-2021-2022学年华东师大版数学七年级下册(word版含答案)
文档属性
| 名称 | 10.4 中心对称-课堂练习-2021-2022学年华东师大版数学七年级下册(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 307.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 00:00:00 | ||
图片预览



文档简介
2021-2022年初中数学七年级下册同步(华东师大版)
10.4中心对称-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个银行标志中,是中心对称图形的标志是( )
A. B. C. D.
2.已知点P(-1-2a,2a-4)关于原点的对称点在第一象限,则整数a的值为( )
A.1 B.0
C.0,1 D.0,1,2
3.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
4.如图,点A,B,C的坐标分别为(0,﹣1),(0,2),(3,0).从下面四个点M(3,3),N(3,﹣3),P(﹣3,0),Q(﹣3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.M B.N C.P D.Q
5.已知点与点关于轴对称,点与点关于原点对称,则点的坐标为( )
A. B. C. D.
6.△ABC和 关于点O对称,下列结论不正确的是( ).
A.AO=
B.AB∥
C.CO=BO
D.∠BAC=∠
二、填空题
7.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和________等.
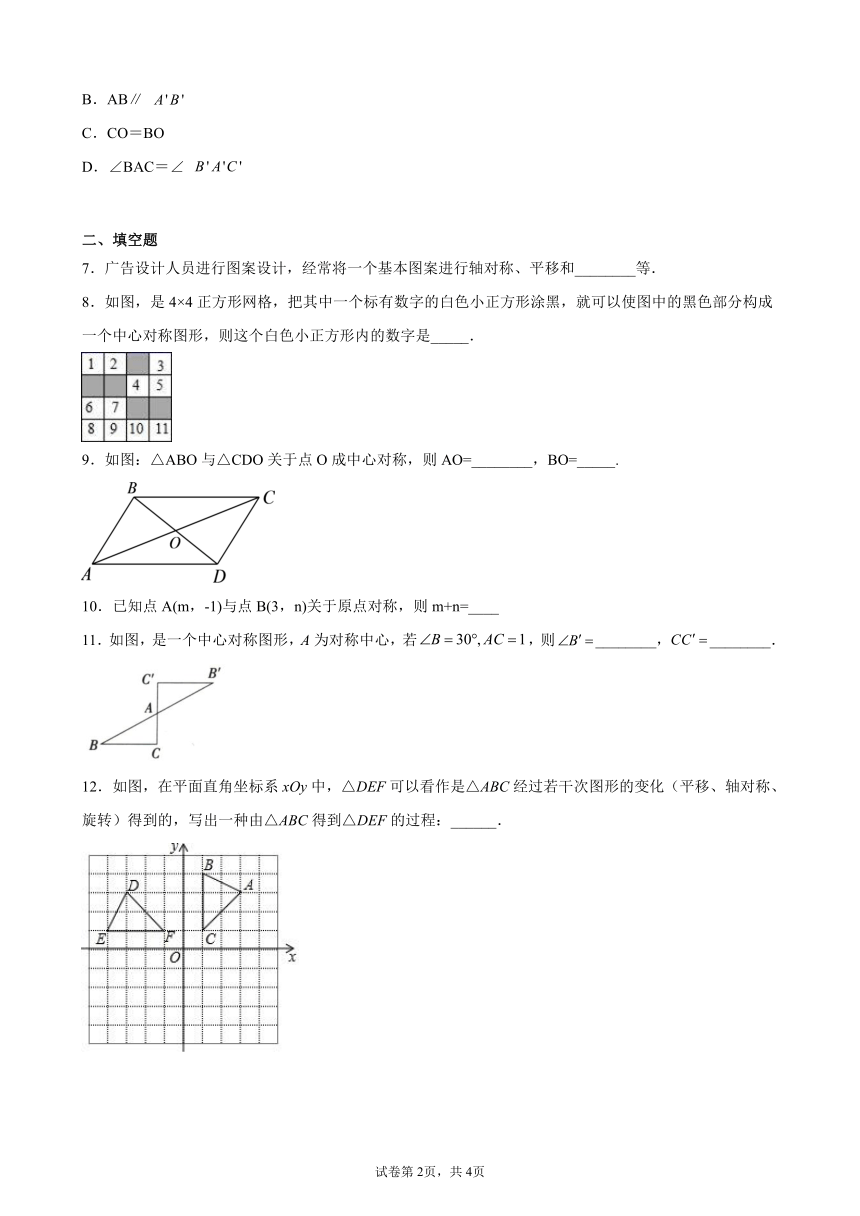
8.如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____.
9.如图:△ABO与△CDO关于点O成中心对称,则AO=________,BO=_____.
10.已知点A(m,-1)与点B(3,n)关于原点对称,则m+n=____
11.如图,是一个中心对称图形,A为对称中心,若,则________,________.
12.如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:______.
三、解答题
13.图中的两个四边形关于某点对称,找出它们的对称中心.
14.在我国的建筑中,很多建筑图形具有对称性,如图是一个破损瓷砖的图案,请把它补画成中心对称图形.
15.如图,与关于点O成中心对称,请你写出两个三角形的对应点、对应线段、对应角和对称中心.
16.已知点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,求a与b的值.
17.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称;
(2)若△ADC的面积为4,求△ABE的面积.
18.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:A.是中心对称图形,故此选项符合题意;
B.不是中心对称图形,故此选项不合题意;
C.不是中心对称图形,故此选项不合题意;
D.不是中心对称图形,故此选项不合题意;
故选:A.
2.C
【解析】解:∵点P( 1 2a,2a 4)关于原点对称的点在第一象限,
∴点P在第三象限,
∴ ,
解得:∵a为整数,
∴a=0或1.
故选C.
3.A
【解析】如图,连接HC和DE交于O1,
故选A.
4.C
【解析】解:根据平行四边形的判定,知A、B、D都能够和已知的三个点组成平行四边形,则一定是中心对称图形.
故选C.
5.D
【解析】解:由点与点关于轴对称可得,由点与点关于原点对称可得点的坐标为.
故选D
6.C
【解析】点C与点B不是对称点,所以线段CO不一定与线段OB相等.
故选C.
7.旋转
【解析】几何变换包括:平移、轴对称、旋转.
故答案为旋转.
8.9
【解析】如图,把标有数字9的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
故答案为9.
9.CO; DO
【解析】∵△ABO和△CDO关于点O成中心对称,
∴△ABO≌△CDO,
∴AO=CO,BO=DO,
故答案为:CO;DO.
10.-2
【解析】点A(m,-1)与点B(3,n)关于原点对称,
∴m =-3,n=1,
∴m+n=-2,
故答案为:-2.
11.30° 2
【解析】解:∵A为对称中心,
∴绕点A旋转能与重合,
∴,
∴,,
∴.
12.△ABC绕C点逆时针旋转90°,并向左平移2个单位得到△DEF
【解析】
由图可知,把△ABC绕点O逆时针旋转90°可得到△DEF.
13.见解析
【解析】解:如图,点O即为所求
14.图见解析.
【解析】解:根据中心对称图形的性质直接画出即可.
15.见解析
【解析】解:对称中心为点O;
对应点分别是:A和D,B和E,C和F;
对应线段分别是:和,和,和;
对应角分别是:和,和,和.
16.a=-1,b=2.
【解析】根据题意,得(2a+2)+(2b-4)=0, (3-3b)+(3a+6)=0,
解得:a=-1,b=2.
17.(1)图中△ADC和三角形EDB成中心对称;(2)8.
【解析】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8.
18.(0,);B(-2,4)C(-2,2)(2,1)(2,3).
【解析】(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
答案第1页,共2页
答案第1页,共2页
10.4中心对称-课堂练习
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.下列四个银行标志中,是中心对称图形的标志是( )
A. B. C. D.
2.已知点P(-1-2a,2a-4)关于原点的对称点在第一象限,则整数a的值为( )
A.1 B.0
C.0,1 D.0,1,2
3.如图,四边形ABCD与四边形FGHE关于一个点成中心对称,则这个点是( )
A.O1 B.O2 C.O3 D.O4
4.如图,点A,B,C的坐标分别为(0,﹣1),(0,2),(3,0).从下面四个点M(3,3),N(3,﹣3),P(﹣3,0),Q(﹣3,1)中选择一个点,以A,B,C与该点为顶点的四边形不是中心对称图形,则该点是( )
A.M B.N C.P D.Q
5.已知点与点关于轴对称,点与点关于原点对称,则点的坐标为( )
A. B. C. D.
6.△ABC和 关于点O对称,下列结论不正确的是( ).
A.AO=
B.AB∥
C.CO=BO
D.∠BAC=∠
二、填空题
7.广告设计人员进行图案设计,经常将一个基本图案进行轴对称、平移和________等.
8.如图,是4×4正方形网格,把其中一个标有数字的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形,则这个白色小正方形内的数字是_____.
9.如图:△ABO与△CDO关于点O成中心对称,则AO=________,BO=_____.
10.已知点A(m,-1)与点B(3,n)关于原点对称,则m+n=____
11.如图,是一个中心对称图形,A为对称中心,若,则________,________.
12.如图,在平面直角坐标系xOy中,△DEF可以看作是△ABC经过若干次图形的变化(平移、轴对称、旋转)得到的,写出一种由△ABC得到△DEF的过程:______.
三、解答题
13.图中的两个四边形关于某点对称,找出它们的对称中心.
14.在我国的建筑中,很多建筑图形具有对称性,如图是一个破损瓷砖的图案,请把它补画成中心对称图形.
15.如图,与关于点O成中心对称,请你写出两个三角形的对应点、对应线段、对应角和对称中心.
16.已知点A(2a+2,3-3b)与点B(2b-4,3a+6)关于坐标原点对称,求a与b的值.
17.如图,D是△ABC边BC的中点,连接AD并延长到点E,使DE=AD,连接BE.
(1)图中哪两个图形成中心对称;
(2)若△ADC的面积为4,求△ABE的面积.
18.如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A, D1 ,D三点的坐标分别是(0,4),(0,3),(0,2).
(1)对称中心的坐标;
(2)写出顶点B, C, B1 , C1的坐标.
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】解:A.是中心对称图形,故此选项符合题意;
B.不是中心对称图形,故此选项不合题意;
C.不是中心对称图形,故此选项不合题意;
D.不是中心对称图形,故此选项不合题意;
故选:A.
2.C
【解析】解:∵点P( 1 2a,2a 4)关于原点对称的点在第一象限,
∴点P在第三象限,
∴ ,
解得:
∴a=0或1.
故选C.
3.A
【解析】如图,连接HC和DE交于O1,
故选A.
4.C
【解析】解:根据平行四边形的判定,知A、B、D都能够和已知的三个点组成平行四边形,则一定是中心对称图形.
故选C.
5.D
【解析】解:由点与点关于轴对称可得,由点与点关于原点对称可得点的坐标为.
故选D
6.C
【解析】点C与点B不是对称点,所以线段CO不一定与线段OB相等.
故选C.
7.旋转
【解析】几何变换包括:平移、轴对称、旋转.
故答案为旋转.
8.9
【解析】如图,把标有数字9的白色小正方形涂黑,就可以使图中的黑色部分构成一个中心对称图形.
故答案为9.
9.CO; DO
【解析】∵△ABO和△CDO关于点O成中心对称,
∴△ABO≌△CDO,
∴AO=CO,BO=DO,
故答案为:CO;DO.
10.-2
【解析】点A(m,-1)与点B(3,n)关于原点对称,
∴m =-3,n=1,
∴m+n=-2,
故答案为:-2.
11.30° 2
【解析】解:∵A为对称中心,
∴绕点A旋转能与重合,
∴,
∴,,
∴.
12.△ABC绕C点逆时针旋转90°,并向左平移2个单位得到△DEF
【解析】
由图可知,把△ABC绕点O逆时针旋转90°可得到△DEF.
13.见解析
【解析】解:如图,点O即为所求
14.图见解析.
【解析】解:根据中心对称图形的性质直接画出即可.
15.见解析
【解析】解:对称中心为点O;
对应点分别是:A和D,B和E,C和F;
对应线段分别是:和,和,和;
对应角分别是:和,和,和.
16.a=-1,b=2.
【解析】根据题意,得(2a+2)+(2b-4)=0, (3-3b)+(3a+6)=0,
解得:a=-1,b=2.
17.(1)图中△ADC和三角形EDB成中心对称;(2)8.
【解析】解:(1)图中△ADC和三角形EDB成中心对称;
(2)∵△ADC和三角形EDB成中心对称,△ADC的面积为4,
∴△EDB的面积也为4,
∵D为BC的中点,
∴△ABD的面积也为4,
所以△ABE的面积为8.
18.(0,);B(-2,4)C(-2,2)(2,1)(2,3).
【解析】(1)根据对称中心的性质,可得
对称中心的坐标是D1D的中点,
∵D1,D的坐标分别是(0,3),(0,2),
∴对称中心的坐标是(0,2.5).
(2)∵A,D的坐标分别是(0,4),(0,2),
∴正方形ABCD与正方形A1B1C1D1的边长都是:4﹣2=2,
∴B,C的坐标分别是(﹣2,4),(﹣2,2),
∵A1D1=2,D1的坐标是(0,3),
∴A1的坐标是(0,1),
∴B1,C1的坐标分别是(2,1),(2,3),
综上,可得顶点B,C,B1,C1的坐标分别是(﹣2,4),(﹣2,2),(2,1),(2,3).
答案第1页,共2页
答案第1页,共2页
