1.1.1等腰三角形(1) 课件(共28张PPT)
文档属性
| 名称 | 1.1.1等腰三角形(1) 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 20:43:53 | ||
图片预览






文档简介
(共28张PPT)
1.1.1 等腰三角形(1)
第一章
三角形的证明
2021-2022学年八年级数学下册同步(北师大版)
学习目标
1.进一步了解“8条基本事实”,学会证明的基本步骤和书写格式.
2.能证明:“AAS”这一全等的判定定理,能利用全等三角形的性质去证明等腰三角形的有关性质定理及其推论.
3.灵活运用等腰三角形的性质进行计算和证明.
导入新课
欣赏生活中的三角形
它们是否具有一般三角形所不具备的特有的性质?
这些三角形有什么共同特点呢?
讲授新课
全等三角形的判定和性质
问题 在八上的“平行线的证明”这一章中,我们学了哪8条基本事实?
1.两点确定一条直线;
2.两点之间线段最短;
3.同一平面内,过一点有且只有一条直线与已知直线垂直;
4.同位角相等,两直线平行;
5.过直线外一点有且只有一条直线与这条直线平行;
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等.
讲授新课
想一想:在探索三角形全等的条件时,我们已经探索过“两角分别对应相等且其中一组等角的对边相等的两个三角形全等”这一结论,你能用已有的基本事实和定理证明这一结论吗?
聪明如我的你们
一定可以搞定哦!
注意对于一个命题的证明,需要哪三部曲哦?
讲授新课
你能证明下面的推论吗?
推论:两角及其中一角的对边对应相等的两个三角形全等.(AAS)
证明文字命题的步骤:
(1)画图;
(2)写“已知”、“求证”;
(3)证明命题.(根据公理或定理证明)
讲授新课
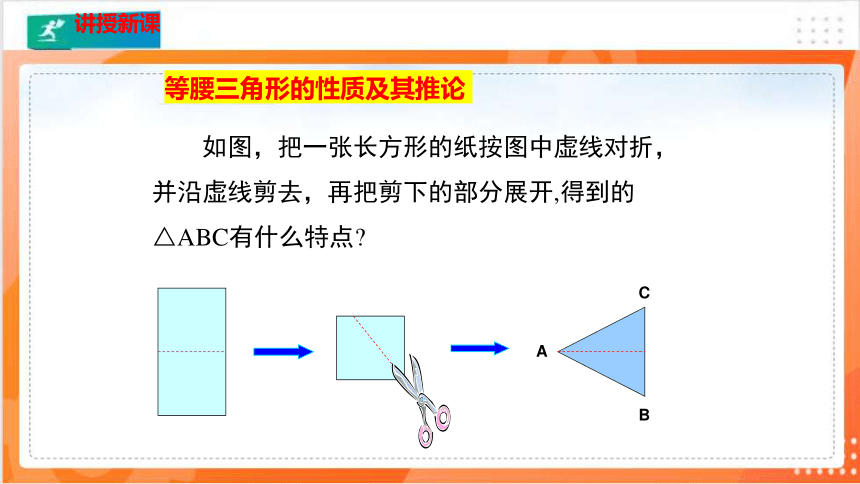
证明:两角及其中一角的对边对应相等的两个三角形全等.
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°)
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E)
∵∠A=∠D,∠B=∠E(已知) ∴∠C=∠F(等量代换)
∵ 在△ABC和△DEF中,∠B=∠E , BC=EF ,∠C=∠F
∴△ABC≌△DEF(ASA)
F
E
D
C
B
A
讲授新课
新知归纳;
定理 两角分别相等且其中一组 等角的对边相等的两个三角形全等。(AAS)
根据全等三角形的定义,我们可以得到
全等三角形性质定理 全等三角形的对应边相等、对应角相等。
讲授新课
等腰三角形的性质及其推论
如图,把一张长方形的纸按图中虚线对折,并沿虚线剪去,再把剪下的部分展开,得到的△ABC有什么特点
A
C
B
讲授新课
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两条
边都叫做腰,另一边叫做底边,
两腰的夹角叫做顶角,腰和底
边的夹角叫做底角.
A
B
C
底边
腰
腰
顶角
底角
讲授新课
问题1:你还记得我们探索过的等腰三角形的性质吗
推论:等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
问题2:你能利用已有的公理和定理证明这些结论吗
定理:等腰三角形的两个底角相等.
(等边对等角)
讲授新课
等腰三角形的两个底角相等.
A
B
C
已知:△ABC中,AB=AC,
求证:∠B= C.
思考:如何构造两个全等的三角形?
定理:等腰三角形的两个底角相等(等边对等角).
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
讲授新课
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
找底边BC的中点D,连接AD,
则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一:作底边上的中线
还有其他的证法吗?
讲授新课
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
讲授新课
结论
定理 等腰三角形的两个底角相等.
这一定理可简述为:“等边对等角”.
思考:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到哪些相等的线段和相等的角?
讲授新课
∵△BAD≌ △CAD,
∴由全等三角形的性质易得
BD=CD,
∠BAD=∠CAD,
∠ADB=∠ADC,
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90°.
A
B
C
D
AD是底边BC上的中线
AD是顶角∠BAC的角平分线
AD是底边BC上的高线
线段AD的性质
讲授新课
结论
推论 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
(1)∵AB=AC,AD⊥BC
∴ (三线合一)
(2)∵AB=AC,BD=CD
∴_________________________(三线合一)
(3)∵AB=AC, ∠BAD=∠CAD
∴____________________ (三线合一)
BD=CD,∠BAD=∠CAD
AD⊥BC,∠BAD=∠CAD
AD⊥BC ,BD=CD
D
C
B
A
当堂检测
1.一个等腰三角形的顶角是50°,则它的底角是( )
A
A.65° B.70° C.75° D.100°
2.如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD=( )
D
A.40° B.50° C.60° D.70°
当堂检测
4.如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH= ( )
A.50° B.60°
C.70° D.80°
B
3.如图, 在△ABC中,AC=BC,用尺规作CF⊥AB,交AB于 点G,若∠BCG=50°,则∠A的度数为 ( )
A.40° B.45°
C.50° D.60°
A
当堂检测
5.如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 ( )5.
A.25° B.20°
C.30° D.15°
D
6.如图,已知AD=BC,∠1=∠2,则下列说法正确的是 ( )
A.BD=AC B.∠D=∠C
C.∠DAB=∠CBA D.以上说法都不对
D
当堂检测
7.如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=70°,则∠B=( )
A
A.70° B.30° C.40° D.20°
8.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与
BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度
数为( )
A.30° B.15° C.25° D.20°
D
当堂检测
9.如图,在△ABC中,AB=AC,∠A=30°,直线m∥n,顶点C在直线n上,直线m交AB于点D,交AC于点E,若∠1=150°,则∠2的度数是( )
A.45° B.40° C.35° D.30°
A
当堂检测
10.如图,△ABC中,AB=AC,垂足为点D,若∠BAC=70°,则∠BAD= .
35°
11.(1)若等腰三角形的一个底角为72°,则这个等腰三角形的顶角为_________.
(2)在△ABC中,AB=AC,∠A=40°,则∠B=_______°.
36°
70
当堂检测
12.如图所示,F、C在线段BE上,且∠1=∠2,BC=EF.若要根据“SAS”使△ABC≌△DEF,还需要补充的条件是 .
AC=DF
当堂检测
13.如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
解:∵AB=AC,∴∠ABC=∠C,
∵∠C=2∠A, 设∠A=x,则∠ABC=∠C=2x,
由x+2x+2x=180°得x=36°,
∴∠A=36°,∠C=72°,
∵BD是AC边上的高,∴BD⊥AC,即∠BDC=90°,
∴∠DBC=90°-∠C=18°.
课堂小结
等腰三角形
性质
等边对等角
推论
三线合一
全等三角形
判定
SSS,SAS,ASA,AAS
性质
对应边相等,对应角相等
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
https://www.21cnjy.com/help/help_extract.php
1.1.1 等腰三角形(1)
第一章
三角形的证明
2021-2022学年八年级数学下册同步(北师大版)
学习目标
1.进一步了解“8条基本事实”,学会证明的基本步骤和书写格式.
2.能证明:“AAS”这一全等的判定定理,能利用全等三角形的性质去证明等腰三角形的有关性质定理及其推论.
3.灵活运用等腰三角形的性质进行计算和证明.
导入新课
欣赏生活中的三角形
它们是否具有一般三角形所不具备的特有的性质?
这些三角形有什么共同特点呢?
讲授新课
全等三角形的判定和性质
问题 在八上的“平行线的证明”这一章中,我们学了哪8条基本事实?
1.两点确定一条直线;
2.两点之间线段最短;
3.同一平面内,过一点有且只有一条直线与已知直线垂直;
4.同位角相等,两直线平行;
5.过直线外一点有且只有一条直线与这条直线平行;
6.两边及其夹角分别相等的两个三角形全等;
7.两角及其夹边分别相等的两个三角形全等;
8.三边分别相等的两个三角形全等.
讲授新课
想一想:在探索三角形全等的条件时,我们已经探索过“两角分别对应相等且其中一组等角的对边相等的两个三角形全等”这一结论,你能用已有的基本事实和定理证明这一结论吗?
聪明如我的你们
一定可以搞定哦!
注意对于一个命题的证明,需要哪三部曲哦?
讲授新课
你能证明下面的推论吗?
推论:两角及其中一角的对边对应相等的两个三角形全等.(AAS)
证明文字命题的步骤:
(1)画图;
(2)写“已知”、“求证”;
(3)证明命题.(根据公理或定理证明)
讲授新课
证明:两角及其中一角的对边对应相等的两个三角形全等.
已知:如图,∠A=∠D,∠B=∠E,BC=EF.
求证:△ABC≌△DEF.
证明:∵∠A+∠B+∠C=180°,
∠D+∠E+∠F=180°(三角形内角和等于180°)
∴∠C=180°-(∠A+∠B),∠F=180°-(∠D+∠E)
∵∠A=∠D,∠B=∠E(已知) ∴∠C=∠F(等量代换)
∵ 在△ABC和△DEF中,∠B=∠E , BC=EF ,∠C=∠F
∴△ABC≌△DEF(ASA)
F
E
D
C
B
A
讲授新课
新知归纳;
定理 两角分别相等且其中一组 等角的对边相等的两个三角形全等。(AAS)
根据全等三角形的定义,我们可以得到
全等三角形性质定理 全等三角形的对应边相等、对应角相等。
讲授新课
等腰三角形的性质及其推论
如图,把一张长方形的纸按图中虚线对折,并沿虚线剪去,再把剪下的部分展开,得到的△ABC有什么特点
A
C
B
讲授新课
定义:两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两条
边都叫做腰,另一边叫做底边,
两腰的夹角叫做顶角,腰和底
边的夹角叫做底角.
A
B
C
底边
腰
腰
顶角
底角
讲授新课
问题1:你还记得我们探索过的等腰三角形的性质吗
推论:等腰三角形顶角的平分线,底边上的中线 底边上的高互相重合(三线合一).
问题2:你能利用已有的公理和定理证明这些结论吗
定理:等腰三角形的两个底角相等.
(等边对等角)
讲授新课
等腰三角形的两个底角相等.
A
B
C
已知:△ABC中,AB=AC,
求证:∠B= C.
思考:如何构造两个全等的三角形?
定理:等腰三角形的两个底角相等(等边对等角).
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
讲授新课
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
找底边BC的中点D,连接AD,
则BD=CD.
AB=AC ( 已知 ),
BD=CD ( 已作 ),
AD=AD (公共边),
∴ △BAD≌ △CAD (SSS).
∴ ∠B= ∠C (全等三角形的对应角相等).
在△BAD和△CAD中
方法一:作底边上的中线
还有其他的证法吗?
讲授新课
已知: 如图,在△ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中
讲授新课
结论
定理 等腰三角形的两个底角相等.
这一定理可简述为:“等边对等角”.
思考:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到哪些相等的线段和相等的角?
讲授新课
∵△BAD≌ △CAD,
∴由全等三角形的性质易得
BD=CD,
∠BAD=∠CAD,
∠ADB=∠ADC,
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90°.
A
B
C
D
AD是底边BC上的中线
AD是顶角∠BAC的角平分线
AD是底边BC上的高线
线段AD的性质
讲授新课
结论
推论 等腰三角形顶角的平分线、底边上的中线、底边上的高线互相重合(三线合一).
(1)∵AB=AC,AD⊥BC
∴ (三线合一)
(2)∵AB=AC,BD=CD
∴_________________________(三线合一)
(3)∵AB=AC, ∠BAD=∠CAD
∴____________________ (三线合一)
BD=CD,∠BAD=∠CAD
AD⊥BC,∠BAD=∠CAD
AD⊥BC ,BD=CD
D
C
B
A
当堂检测
1.一个等腰三角形的顶角是50°,则它的底角是( )
A
A.65° B.70° C.75° D.100°
2.如图,在△ABC中,AB=AC,∠A=40°,CD∥AB,则∠BCD=( )
D
A.40° B.50° C.60° D.70°
当堂检测
4.如图,已知∠AOB=10°,且OC=CD=DE=EF=FG=GH,则∠BGH= ( )
A.50° B.60°
C.70° D.80°
B
3.如图, 在△ABC中,AC=BC,用尺规作CF⊥AB,交AB于 点G,若∠BCG=50°,则∠A的度数为 ( )
A.40° B.45°
C.50° D.60°
A
当堂检测
5.如图,AB=AC,AB的垂直平分线MN交AC于点D,若∠C=65°,则∠DBC的度数是 ( )5.
A.25° B.20°
C.30° D.15°
D
6.如图,已知AD=BC,∠1=∠2,则下列说法正确的是 ( )
A.BD=AC B.∠D=∠C
C.∠DAB=∠CBA D.以上说法都不对
D
当堂检测
7.如图,AB∥CD,点E在线段BC上,CD=CE,若∠D=70°,则∠B=( )
A
A.70° B.30° C.40° D.20°
8.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与
BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度
数为( )
A.30° B.15° C.25° D.20°
D
当堂检测
9.如图,在△ABC中,AB=AC,∠A=30°,直线m∥n,顶点C在直线n上,直线m交AB于点D,交AC于点E,若∠1=150°,则∠2的度数是( )
A.45° B.40° C.35° D.30°
A
当堂检测
10.如图,△ABC中,AB=AC,垂足为点D,若∠BAC=70°,则∠BAD= .
35°
11.(1)若等腰三角形的一个底角为72°,则这个等腰三角形的顶角为_________.
(2)在△ABC中,AB=AC,∠A=40°,则∠B=_______°.
36°
70
当堂检测
12.如图所示,F、C在线段BE上,且∠1=∠2,BC=EF.若要根据“SAS”使△ABC≌△DEF,还需要补充的条件是 .
AC=DF
当堂检测
13.如图,在△ABC中,AB=AC,∠C=2∠A,BD是AC边上的高,求∠A和∠DBC的度数.
解:∵AB=AC,∴∠ABC=∠C,
∵∠C=2∠A, 设∠A=x,则∠ABC=∠C=2x,
由x+2x+2x=180°得x=36°,
∴∠A=36°,∠C=72°,
∵BD是AC边上的高,∴BD⊥AC,即∠BDC=90°,
∴∠DBC=90°-∠C=18°.
课堂小结
等腰三角形
性质
等边对等角
推论
三线合一
全等三角形
判定
SSS,SAS,ASA,AAS
性质
对应边相等,对应角相等
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
