1.2.2直角三角形(2) 课件(共27张PPT)
文档属性
| 名称 | 1.2.2直角三角形(2) 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 688.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 21:00:38 | ||
图片预览





文档简介
(共27张PPT)
1.2.2直角三角形(2)
第一章
三角形的证明
2021-2022学年八年级数学下册同步(北师大版)
学习目标
1 经历直角三角形全等的“HL”的判定定理探索过程,进一步理解证明的必要性,掌握并利用“HL”定理解决实际问题.
2 能用尺规完成作图:已知一条直角边和斜边作直角三角形.
导入新课
(2)两边分别相等且其中一组等边的对角分别相等的两个三 角形全等吗?
(3)如果其中一组等边所对的角是直角呢?
不一定全等.
思考:(1)我们学过的判定三角形全等的方法?
SSS、 SAS、 ASA 、AAS.
这节课我们一起来探索并证明直角三角形全等的判定.
导入新课
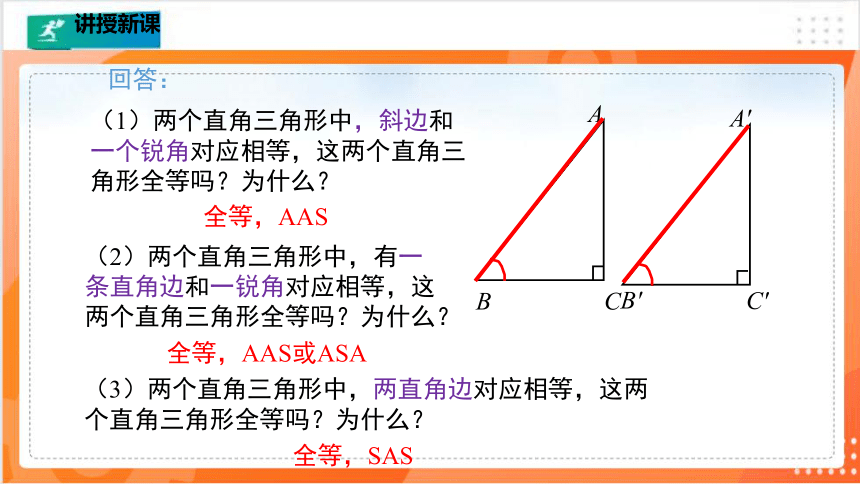
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量. 你能帮工作人员想个办法吗?
讲授新课
直角三角形全等的判定(“斜边、直角边”定理)
思考:
C
B
A
如图,在Rt△ABC中,∠C =90°,直角边是AC、BC,斜边是AB.
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
完全适用
讲授新课
A
B
C
A′
B′
C′
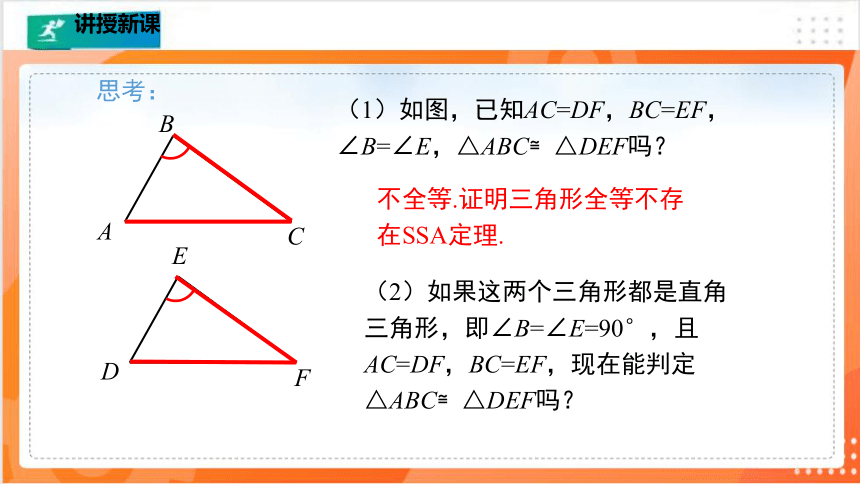
(1)两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
(2)两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
(3)两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
回答:
全等,AAS
全等,AAS或ASA
全等,SAS
讲授新课
(1)如图,已知AC=DF,BC=EF,
∠B=∠E,△ABC≌△DEF吗?
A
B
C
D
E
F
思考:
不全等.证明三角形全等不存在SSA定理.
(2)如果这两个三角形都是直角三角形,即∠B=∠E=90°,且AC=DF,BC=EF,现在能判定△ABC≌△DEF吗?
讲授新课
做一做:
已知一条直角边和斜边,求作一个直角三角形.
任意画出一个Rt△ABC,使∠C=90°.
再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,
把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
讲授新课
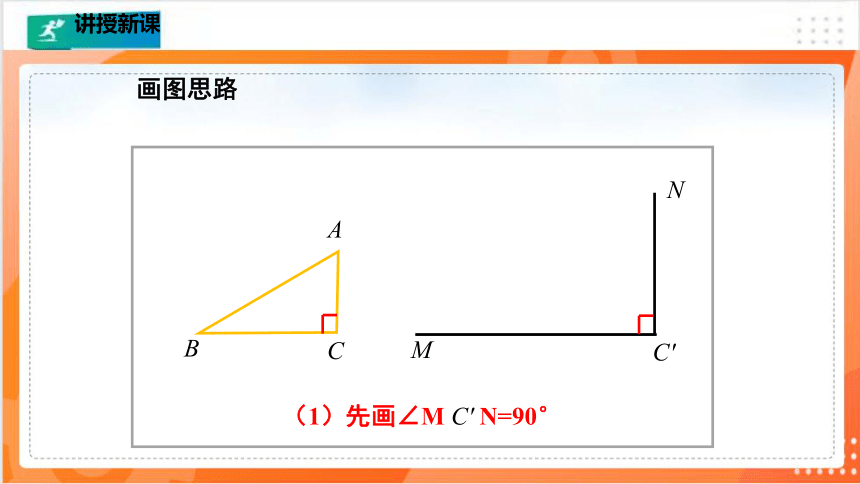
画图思路
(1)先画∠M C′ N=90°
A
B
C
M
C′
N
讲授新课
画图思路
(2)在射线C′M上截取B′C′=BC
M
C′
A
B
C
N
B′
M
C′
讲授新课
画图思路
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′
M
C′
A
B
C
N
B′
A′
讲授新课
画图思路
(4)连接A′B′
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
讲授新课
猜想:斜边和一条直角边对应相等的两个直角三角形全等;
证明:∵△ABC中,∠C=90°
∴BC2=AB2-AC2(勾股定理)
同理,B′C′2=A′B′2-A′C′2 .
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′(SSS).
已知:如图, 在△ABC和△A′B′C′中, ∠C=∠C′=90°, AC=A′C ′, AB=A′B′
求证:△ABC≌△A′B′C′ .
A
B
C
A′
B′
C′
知识要点
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
讲授新课
例:有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小关系?
解:由题意,得,∠BAC=∠EDF=90°
BC=EF,AC=DF
∴Rt△BAC≌Rt△EDF (HL)
∴∠B=∠DEF (全等三角形对应角相等)
∵∠DEF+∠F=90°(直角三角形两锐角互余)
∴∠B+∠F=90°
讲授新课
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
当堂检测
1.如图,一张长方形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是( )
A.30° B.60° C.90° D.120°
2.由下列 条件不能判定△ABC是直角三角形的是( )
A.∠A=37°,∠C=53° B.∠A=34°,∠B=56°
C.∠B=42°,∠C=38° D.∠A=72°,∠B=18°
C
C
当堂检测
3.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
D
4.如图,点P是∠BAC内一点,PE⊥AC于点E,PF⊥AB于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
A.HL B.ASA C.AAS D.SAS
A
当堂检测
5.不能判断两个直角三角形全等的条件是( )
A.两锐角对应相等的两个直角三角形
B.一锐角和锐角所对的直角边分别对应相等的两个直角三角形
C.两条直角边分别对应相等的两个直角三角形
D.一条直角边和斜边分别对应相等的两个直角三角形
A
当堂检测
6. 如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA
C.SSA D.HL
7.如图,点D,A,E在直线l上,AB=AC,BD⊥l于点D,CE⊥ l于 点E,且BD=AE,若BD=3,CE=5,则DE= .
8
D
当堂检测
8.已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E.F,且DE=DF,
求证:△ABC是等腰三角形
证明:∵ D是△ABC的BC边的中点
∴BD=CD
∵ DE⊥AC,DF⊥AB
∴∠1=∠2=90°
∵BD=CD,DE=DF
∴Rt△BDF≌Rt△CDE (HL)
∴∠B=∠C
∴△ABC是等腰三角形
1
2
当堂检测
9.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为EF,且DE=BF,求证:(1)AE=CF(2)AB∥CD
证明:(1)∵ DE⊥AC,BF⊥AC
∴∠1=∠2=90°
∵AB=CD,DE=BF
∴Rt△ABF≌Rt△CDE (HL)
∴AF=CE
∴AF-EF=CE-EF
即AE=CF
(2) ∵Rt△ABF≌Rt△CDE (HL)
∴∠A=∠C ∴AB∥CD(内错角相等,两直线平行)
1
2
当堂检测
10.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=3 0°,求∠ACF的度数.
当堂检测
解:(1)证明:∵∠ABC=90 °,∴∠CBF=∠ABE=90 °.
在Rt△ABE和Rt△CBF中,
∵AE=CF,AB=CB, ∴Rt△AB E≌Rt△CBF(HL).
(2)∵AB=CB,∠ABC=90 °,∴∠CAB=∠ACB=45 °.
∴∠BAE=∠CAB-∠CAE=4 5 °-30 °=15 °.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15 °.
∴∠ACF=∠ BCF+∠ACB=15 °+45 °=60 °.
课堂小结
斜边和一条直角边对应相等的两个直角三角形全等.
“斜边、直角边”
在直角三角形中
内容
前提条件
在直角三角形中,只要有两边对应相等,则直角三角形全等
使用方法
https://www.21cnjy.com/help/help_extract.php
1.2.2直角三角形(2)
第一章
三角形的证明
2021-2022学年八年级数学下册同步(北师大版)
学习目标
1 经历直角三角形全等的“HL”的判定定理探索过程,进一步理解证明的必要性,掌握并利用“HL”定理解决实际问题.
2 能用尺规完成作图:已知一条直角边和斜边作直角三角形.
导入新课
(2)两边分别相等且其中一组等边的对角分别相等的两个三 角形全等吗?
(3)如果其中一组等边所对的角是直角呢?
不一定全等.
思考:(1)我们学过的判定三角形全等的方法?
SSS、 SAS、 ASA 、AAS.
这节课我们一起来探索并证明直角三角形全等的判定.
导入新课
舞台背景的形状是两个直角三角形,为了美观,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量. 你能帮工作人员想个办法吗?
讲授新课
直角三角形全等的判定(“斜边、直角边”定理)
思考:
C
B
A
如图,在Rt△ABC中,∠C =90°,直角边是AC、BC,斜边是AB.
前面学过的四种判定三角形全等的方法,对直角三角形是否适用?
完全适用
讲授新课
A
B
C
A′
B′
C′
(1)两个直角三角形中,斜边和一个锐角对应相等,这两个直角三角形全等吗?为什么?
(2)两个直角三角形中,有一条直角边和一锐角对应相等,这两个直角三角形全等吗?为什么?
(3)两个直角三角形中,两直角边对应相等,这两个直角三角形全等吗?为什么?
回答:
全等,AAS
全等,AAS或ASA
全等,SAS
讲授新课
(1)如图,已知AC=DF,BC=EF,
∠B=∠E,△ABC≌△DEF吗?
A
B
C
D
E
F
思考:
不全等.证明三角形全等不存在SSA定理.
(2)如果这两个三角形都是直角三角形,即∠B=∠E=90°,且AC=DF,BC=EF,现在能判定△ABC≌△DEF吗?
讲授新课
做一做:
已知一条直角边和斜边,求作一个直角三角形.
任意画出一个Rt△ABC,使∠C=90°.
再画一个Rt△A ′B ′C ′,使∠C′=90 °,B′C′=BC,A ′B ′=AB,
把画好的Rt△A′B′ C′ 剪下来,放到Rt△ABC上,它们能重合吗?
A
B
C
讲授新课
画图思路
(1)先画∠M C′ N=90°
A
B
C
M
C′
N
讲授新课
画图思路
(2)在射线C′M上截取B′C′=BC
M
C′
A
B
C
N
B′
M
C′
讲授新课
画图思路
(3)以点B′为圆心,AB为半径画弧,交射线C′N于A′
M
C′
A
B
C
N
B′
A′
讲授新课
画图思路
(4)连接A′B′
M
C′
A
B
C
N
B′
A′
思考:通过上面的探究,你能得出什么结论?
讲授新课
猜想:斜边和一条直角边对应相等的两个直角三角形全等;
证明:∵△ABC中,∠C=90°
∴BC2=AB2-AC2(勾股定理)
同理,B′C′2=A′B′2-A′C′2 .
∵AB=A′B′,AC=A′C′,
∴BC=B′C′.
∴ △ABC ≌ △A′B′C′(SSS).
已知:如图, 在△ABC和△A′B′C′中, ∠C=∠C′=90°, AC=A′C ′, AB=A′B′
求证:△ABC≌△A′B′C′ .
A
B
C
A′
B′
C′
知识要点
“斜边、直角边”判定方法
文字语言:
斜边和一条直角边对应相等的两个直角三角形全等
(简写成“斜边、直角边”或“HL”).
几何语言:
A
B
C
A ′
B′
C ′
在Rt△ABC和Rt△ A′B′C′ 中,
∴Rt△ABC ≌ Rt△ A′B′C′ (HL).
“SSA”可以判定两个直角三角形全等,但是“边边”指的是斜边和一直角边,而“角”指的是直角.
AB=A′B′,
BC=B′C′,
讲授新课
例:有两个长度相等的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠B和∠F的大小关系?
解:由题意,得,∠BAC=∠EDF=90°
BC=EF,AC=DF
∴Rt△BAC≌Rt△EDF (HL)
∴∠B=∠DEF (全等三角形对应角相等)
∵∠DEF+∠F=90°(直角三角形两锐角互余)
∴∠B+∠F=90°
讲授新课
方法总结:证明线段相等可通过证明三角形全等解决,作为“HL”公理就是直角三角形独有的判定方法.所以直角三角形的判定方法最多,使用时应该抓住“直角”这个隐含的已知条件.
当堂检测
1.如图,一张长方形纸片,剪去部分后得到一个三角形,则图中∠1+∠2的度数是( )
A.30° B.60° C.90° D.120°
2.由下列 条件不能判定△ABC是直角三角形的是( )
A.∠A=37°,∠C=53° B.∠A=34°,∠B=56°
C.∠B=42°,∠C=38° D.∠A=72°,∠B=18°
C
C
当堂检测
3.如图,点D在△ABC的边AC上,将△ABC沿BD翻折后,点A恰好与点C重合.若BC=5,CD=3,则BD的长为( )
A.1 B.2 C.3 D.4
D
4.如图,点P是∠BAC内一点,PE⊥AC于点E,PF⊥AB于点F,PE=PF,则直接得到△PEA≌△PFA的理由是( )
A.HL B.ASA C.AAS D.SAS
A
当堂检测
5.不能判断两个直角三角形全等的条件是( )
A.两锐角对应相等的两个直角三角形
B.一锐角和锐角所对的直角边分别对应相等的两个直角三角形
C.两条直角边分别对应相等的两个直角三角形
D.一条直角边和斜边分别对应相等的两个直角三角形
A
当堂检测
6. 如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA
C.SSA D.HL
7.如图,点D,A,E在直线l上,AB=AC,BD⊥l于点D,CE⊥ l于 点E,且BD=AE,若BD=3,CE=5,则DE= .
8
D
当堂检测
8.已知:如图,D是△ABC的BC边的中点,DE⊥AC,DF⊥AB,垂足分别是E.F,且DE=DF,
求证:△ABC是等腰三角形
证明:∵ D是△ABC的BC边的中点
∴BD=CD
∵ DE⊥AC,DF⊥AB
∴∠1=∠2=90°
∵BD=CD,DE=DF
∴Rt△BDF≌Rt△CDE (HL)
∴∠B=∠C
∴△ABC是等腰三角形
1
2
当堂检测
9.已知:如图,AB=CD,DE⊥AC,BF⊥AC,垂足分别为EF,且DE=BF,求证:(1)AE=CF(2)AB∥CD
证明:(1)∵ DE⊥AC,BF⊥AC
∴∠1=∠2=90°
∵AB=CD,DE=BF
∴Rt△ABF≌Rt△CDE (HL)
∴AF=CE
∴AF-EF=CE-EF
即AE=CF
(2) ∵Rt△ABF≌Rt△CDE (HL)
∴∠A=∠C ∴AB∥CD(内错角相等,两直线平行)
1
2
当堂检测
10.如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=3 0°,求∠ACF的度数.
当堂检测
解:(1)证明:∵∠ABC=90 °,∴∠CBF=∠ABE=90 °.
在Rt△ABE和Rt△CBF中,
∵AE=CF,AB=CB, ∴Rt△AB E≌Rt△CBF(HL).
(2)∵AB=CB,∠ABC=90 °,∴∠CAB=∠ACB=45 °.
∴∠BAE=∠CAB-∠CAE=4 5 °-30 °=15 °.
由(1)知Rt△ABE≌Rt△CBF,
∴∠BCF=∠BAE=15 °.
∴∠ACF=∠ BCF+∠ACB=15 °+45 °=60 °.
课堂小结
斜边和一条直角边对应相等的两个直角三角形全等.
“斜边、直角边”
在直角三角形中
内容
前提条件
在直角三角形中,只要有两边对应相等,则直角三角形全等
使用方法
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
