1.4.1角平分线(1) 课件(共26张PPT)
文档属性
| 名称 | 1.4.1角平分线(1) 课件(共26张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 775.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 21:00:22 | ||
图片预览





文档简介
(共26张PPT)
1.4.1 角平分线(1)
第一章
三角形的证明
2021-2022学年八年级数学下册同步(北师大版)
学习目标
1.探索证明角平分线的性质和判定.
2.能运用角平分线性质和其判定解决实际问题.
3.经历“探索-发现-猜想-证明”的过程,进一步体会证明的必要性,增强证明意识和能力,发展推理能力.
导入新课
不利用工具,请你将一张用纸片做的角分成两个相等的角. 你有什么办法?
对折
再打开纸片 ,看看折痕与这个角有何关系?
A
O
B
C
导入新课
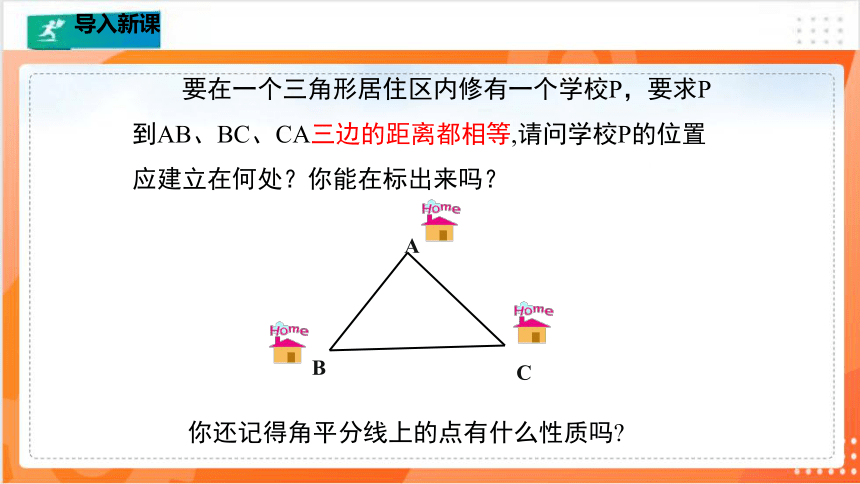
要在一个三角形居住区内修有一个学校P,要求P到AB、BC、CA三边的距离都相等,请问学校P的位置应建立在何处?你能在标出来吗?
A
B
C
你还记得角平分线上的点有什么性质吗
讲授新课
角平分线的性质
还记得角平分线上的点有什么性质吗?你是怎样得到的?请你尝试证明这性质,并与同伴交流.
角的平分线上的点到角的两边的距离相等
讲授新课
思考:角平分线的性质定理和线段垂直平分线的性质定理中都提到了“距离相等”,你认为这两个“距离”含义相同吗?
不相同.
线段垂直平分线的性质定理中“距离”是两点之间的距离,
而角平分线的性质定理中的“距离”指的是点到线的距离,
因此角平分线性质定理中才要求过点作角的两边的垂线.
讲授新课
思路总结:本定理是对三角形全等思路的优化
已知:如图,OC是∠AOB的平分线,点P在OC上,PD丄OA, PE丄OB,垂足分别为D,E.
求证:PD=PE.
A
C
B
O
D
P
E
1
2
证明:∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠PDO=∠PEO=90°.
∵∠1=∠2, OP=OP
∴△PDO≌△PEO ( AAS ).
∴PD=PE (全等三角形的对应边相等).
讲授新课
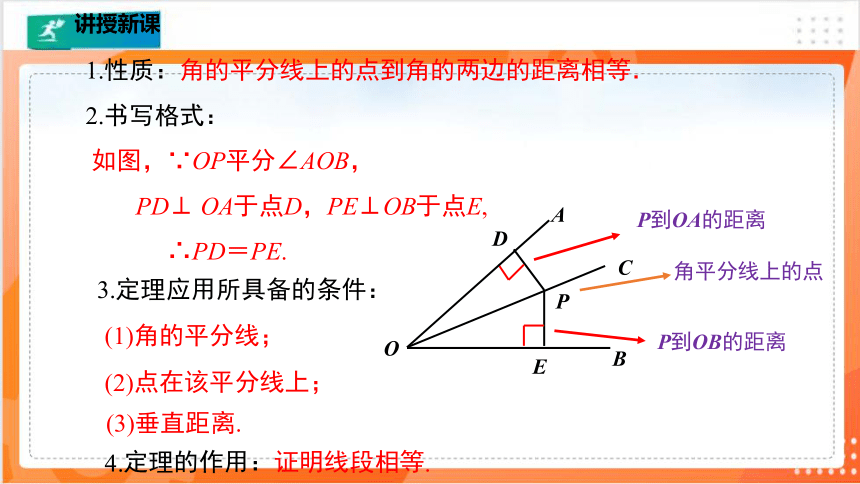
1.性质:角的平分线上的点到角的两边的距离相等.
2.书写格式:
如图,∵OP平分∠AOB,
PD⊥ OA于点D,PE⊥OB于点E,
∴PD=PE.
3.定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
4.定理的作用:证明线段相等.
D
E
P
P到OA的距离
P到OB的距离
角平分线上的点
O
A
C
B
讲授新课
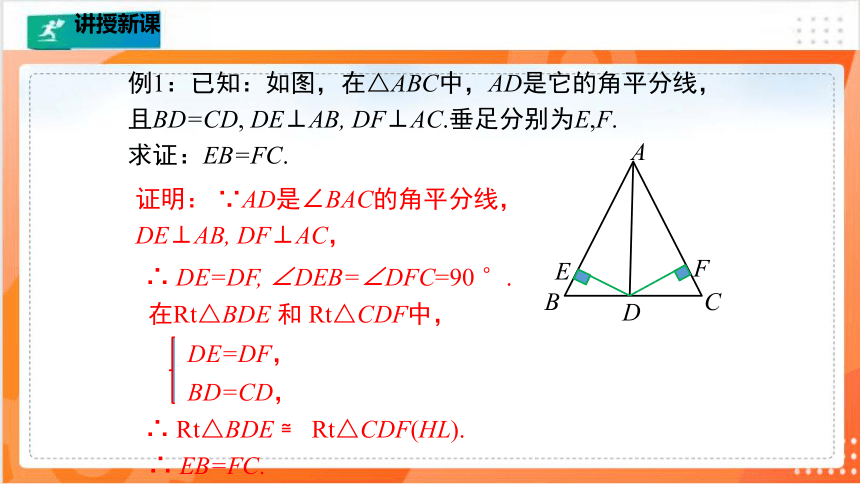
例1:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD, DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
讲授新课
角平分线的判定
想一想:你能写出这个定理的逆命题吗?它是真命题吗?
如果有一个点到角两边的距离相等,那么这个点必在这个角的平分线上.
这个命题是真的吗?如果是假的,怎么修改能成为真的呢?
讲授新课
想一想
如图,点 P是平面内一点,PD⊥OA于D,PE⊥OB于E,点P在∠AOB的角平分线上吗?
上面逆命题的准确说法应该怎样说?
在一个角的内部,到角两边距离相等的点在这个角的平分线上.
讲授新课
已知:如图,点P为∠AOB内一点,PD丄OA,PE丄OB,垂足分别为D,E,且PD=PE.
求证:OP平分∠AOB.
A
C
B
O
D
P
E
1
2
证明:∵PD丄OA, PE丄OB,垂足分别为D,E,
∴∠ODP=∠OEP=90°,
∵PD=PE,OP=OP,
∴Rt△DOP≌ Rt△EOP ( HL ).
∴∠1=∠2 (全等三角形的对应角相等).
∴OP平分∠AOB.
讲授新课
1.判定方法:
角的内部到角的两边的距离相等的点在角的平分线上.
2.书写格式:∵PD⊥OA,PE⊥OB,PD=PE,
∴点P在∠AOB的平分线上(或∠AOC=∠BOC).
3.应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
4.定理的作用:判断点是否在角平分线上.
讲授新课
例2 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求DE的长.
解: ∵DE ⊥ AB,DF ⊥ AC,DE=DF,
∴AD平分∠BAC
又∵ ∠BAC=60°,
∴ ∠BAD=30°.
在Rt △ADE中, ∠AED=90°,AD=10,
∴DE= AD= ×10=5
(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).
归纳总结
图形
已知 条件
结论
P
C
P
C
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
角的平分线的性质
1.如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:
①AS=AR;②QP∥AR;③△BRP≌△CSP.正确的是( )
A.①和② B.②和③
C.①和③ D.全对
A
当堂检测
当堂检测
2. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A
A.3 B.4 C.5 D.6
3. 如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线, ∠BAC=50°, ∠ABC=60°,则∠EAD+∠ACD= ( )
A.75° B.80° C.85° D.90°
A
当堂检测
4、如图,△ABC的两条外角平分线AP,CP相交于点P,PH⊥AC于H;如果∠ABC=60°,
则下列结论:①∠ABP=30°;②∠APC=60°;③PB=2PH;④∠APH=∠BPC,
其中正确的结论个数是 ( )
A.1 B.2
C.3 D.4
D
当堂检测
5.如图,在Rt△ABC中,∠C=90°, ∠B=45°, AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为_______.
a-m
6.如图,BD是∠ABC的平分线,DE⊥AB于点E,△ABC的面积是30 cm2,AB=18 cm,BC=12 cm,则DE=______cm.
2
当堂检测
7. 如图,在△ABC中,AD为其角平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是9 cm2,AB=5 cm,AC=4 cm,求DE的长.
解:∵在△ABC中,
AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF.
∵△ABC的面积是9 cm2,AB=5 cm,AC=4 cm,
∴ ×5DE+ ×4DF=9,
∴DE=DF=2(cm),即DE的长是2 cm.
当堂检测
8. 已知:如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDF=∠PEG=90°.
在Rt△PFD和Rt△PGE中,
∵PF=PG,DF=EG,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE.
∵P是OC上点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
当堂检测
9.如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
(1)则点P到AB的距离为_______.
4
A
B
C
P
D
当堂检测
解:由角平分线的性质,可知,PD=PC=4,
(2)求△APB的面积.
·AB·PD=28.
(3)求 PDB的周长.
A
B
C
P
D
=
解:
课堂小结
角平分线
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
判定定理
在一个角的内部,到角两边距离相等的点在这个角的平分线上
https://www.21cnjy.com/help/help_extract.php
1.4.1 角平分线(1)
第一章
三角形的证明
2021-2022学年八年级数学下册同步(北师大版)
学习目标
1.探索证明角平分线的性质和判定.
2.能运用角平分线性质和其判定解决实际问题.
3.经历“探索-发现-猜想-证明”的过程,进一步体会证明的必要性,增强证明意识和能力,发展推理能力.
导入新课
不利用工具,请你将一张用纸片做的角分成两个相等的角. 你有什么办法?
对折
再打开纸片 ,看看折痕与这个角有何关系?
A
O
B
C
导入新课
要在一个三角形居住区内修有一个学校P,要求P到AB、BC、CA三边的距离都相等,请问学校P的位置应建立在何处?你能在标出来吗?
A
B
C
你还记得角平分线上的点有什么性质吗
讲授新课
角平分线的性质
还记得角平分线上的点有什么性质吗?你是怎样得到的?请你尝试证明这性质,并与同伴交流.
角的平分线上的点到角的两边的距离相等
讲授新课
思考:角平分线的性质定理和线段垂直平分线的性质定理中都提到了“距离相等”,你认为这两个“距离”含义相同吗?
不相同.
线段垂直平分线的性质定理中“距离”是两点之间的距离,
而角平分线的性质定理中的“距离”指的是点到线的距离,
因此角平分线性质定理中才要求过点作角的两边的垂线.
讲授新课
思路总结:本定理是对三角形全等思路的优化
已知:如图,OC是∠AOB的平分线,点P在OC上,PD丄OA, PE丄OB,垂足分别为D,E.
求证:PD=PE.
A
C
B
O
D
P
E
1
2
证明:∵PD丄OA,PE丄OB,垂足分别为D,E,
∴∠PDO=∠PEO=90°.
∵∠1=∠2, OP=OP
∴△PDO≌△PEO ( AAS ).
∴PD=PE (全等三角形的对应边相等).
讲授新课
1.性质:角的平分线上的点到角的两边的距离相等.
2.书写格式:
如图,∵OP平分∠AOB,
PD⊥ OA于点D,PE⊥OB于点E,
∴PD=PE.
3.定理应用所具备的条件:
(1)角的平分线;
(2)点在该平分线上;
(3)垂直距离.
4.定理的作用:证明线段相等.
D
E
P
P到OA的距离
P到OB的距离
角平分线上的点
O
A
C
B
讲授新课
例1:已知:如图,在△ABC中,AD是它的角平分线,且BD=CD, DE⊥AB, DF⊥AC.垂足分别为E,F.
求证:EB=FC.
A
B
C
D
E
F
证明: ∵AD是∠BAC的角平分线, DE⊥AB, DF⊥AC,
∴ DE=DF, ∠DEB=∠DFC=90 °.
在Rt△BDE 和 Rt△CDF中,
DE=DF,
BD=CD,
∴ Rt△BDE ≌ Rt△CDF(HL).
∴ EB=FC.
讲授新课
角平分线的判定
想一想:你能写出这个定理的逆命题吗?它是真命题吗?
如果有一个点到角两边的距离相等,那么这个点必在这个角的平分线上.
这个命题是真的吗?如果是假的,怎么修改能成为真的呢?
讲授新课
想一想
如图,点 P是平面内一点,PD⊥OA于D,PE⊥OB于E,点P在∠AOB的角平分线上吗?
上面逆命题的准确说法应该怎样说?
在一个角的内部,到角两边距离相等的点在这个角的平分线上.
讲授新课
已知:如图,点P为∠AOB内一点,PD丄OA,PE丄OB,垂足分别为D,E,且PD=PE.
求证:OP平分∠AOB.
A
C
B
O
D
P
E
1
2
证明:∵PD丄OA, PE丄OB,垂足分别为D,E,
∴∠ODP=∠OEP=90°,
∵PD=PE,OP=OP,
∴Rt△DOP≌ Rt△EOP ( HL ).
∴∠1=∠2 (全等三角形的对应角相等).
∴OP平分∠AOB.
讲授新课
1.判定方法:
角的内部到角的两边的距离相等的点在角的平分线上.
2.书写格式:∵PD⊥OA,PE⊥OB,PD=PE,
∴点P在∠AOB的平分线上(或∠AOC=∠BOC).
3.应用所具备的条件:
(1)位置关系:点在角的内部;
(2)数量关系:该点到角两边的距离相等.
4.定理的作用:判断点是否在角平分线上.
讲授新课
例2 如图,在△ABC中,∠BAC=60°,点D在BC上,AD=10,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求DE的长.
解: ∵DE ⊥ AB,DF ⊥ AC,DE=DF,
∴AD平分∠BAC
又∵ ∠BAC=60°,
∴ ∠BAD=30°.
在Rt △ADE中, ∠AED=90°,AD=10,
∴DE= AD= ×10=5
(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半).
归纳总结
图形
已知 条件
结论
P
C
P
C
OP平分∠AOB
PD⊥OA于D
PE⊥OB于E
PD=PE
OP平分∠AOB
PD=PE
PD⊥OA于D
PE⊥OB于E
角的平分线的判定
角的平分线的性质
1.如图所示,在△ABC中,P为BC上一点,PR⊥AB,垂足为R,PS⊥AC,垂足为S,AQ=PQ,PR=PS.下面三个结论:
①AS=AR;②QP∥AR;③△BRP≌△CSP.正确的是( )
A.①和② B.②和③
C.①和③ D.全对
A
当堂检测
当堂检测
2. 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,AB=10,S△ABD=15,则CD的长为( )
A
A.3 B.4 C.5 D.6
3. 如图,在△ABC中,AD是BC边上的高,AE,BF分别是∠BAC,∠ABC的平分线, ∠BAC=50°, ∠ABC=60°,则∠EAD+∠ACD= ( )
A.75° B.80° C.85° D.90°
A
当堂检测
4、如图,△ABC的两条外角平分线AP,CP相交于点P,PH⊥AC于H;如果∠ABC=60°,
则下列结论:①∠ABP=30°;②∠APC=60°;③PB=2PH;④∠APH=∠BPC,
其中正确的结论个数是 ( )
A.1 B.2
C.3 D.4
D
当堂检测
5.如图,在Rt△ABC中,∠C=90°, ∠B=45°, AD是∠CAB的平分线,DE⊥AB于E,AB=a,CD=m,则AC的长为_______.
a-m
6.如图,BD是∠ABC的平分线,DE⊥AB于点E,△ABC的面积是30 cm2,AB=18 cm,BC=12 cm,则DE=______cm.
2
当堂检测
7. 如图,在△ABC中,AD为其角平分线,DE⊥AB于点E,DF⊥AC于点F,△ABC的面积是9 cm2,AB=5 cm,AC=4 cm,求DE的长.
解:∵在△ABC中,
AD平分∠BAC,DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF.
∵△ABC的面积是9 cm2,AB=5 cm,AC=4 cm,
∴ ×5DE+ ×4DF=9,
∴DE=DF=2(cm),即DE的长是2 cm.
当堂检测
8. 已知:如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F,G分别是OA,OB上的点,且PF=PG,DF=EG.
求证:OC是∠AOB的平分线.
证明:∵PD⊥OA,PE⊥OB,
∴∠PDF=∠PEG=90°.
在Rt△PFD和Rt△PGE中,
∵PF=PG,DF=EG,
∴Rt△PFD≌Rt△PGE(HL),
∴PD=PE.
∵P是OC上点,PD⊥OA,PE⊥OB,
∴OC是∠AOB的平分线.
当堂检测
9.如图,在Rt△ABC中,AC=BC,∠C=90°,AP平分∠BAC交BC于点P,若PC=4, AB=14.
(1)则点P到AB的距离为_______.
4
A
B
C
P
D
当堂检测
解:由角平分线的性质,可知,PD=PC=4,
(2)求△APB的面积.
·AB·PD=28.
(3)求 PDB的周长.
A
B
C
P
D
=
解:
课堂小结
角平分线
性质定理
一个点:角平分线上的点;
二距离:点到角两边的距离;
两相等:两条垂线段相等
辅助线
添加
过角平分线上一点向两边作垂线段
判定定理
在一个角的内部,到角两边距离相等的点在这个角的平分线上
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
