2021-2022学年湘教版数学八年级下册4.5一次函数的应用课时练习 (word版含答案)
文档属性
| 名称 | 2021-2022学年湘教版数学八年级下册4.5一次函数的应用课时练习 (word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 140.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 09:37:16 | ||
图片预览


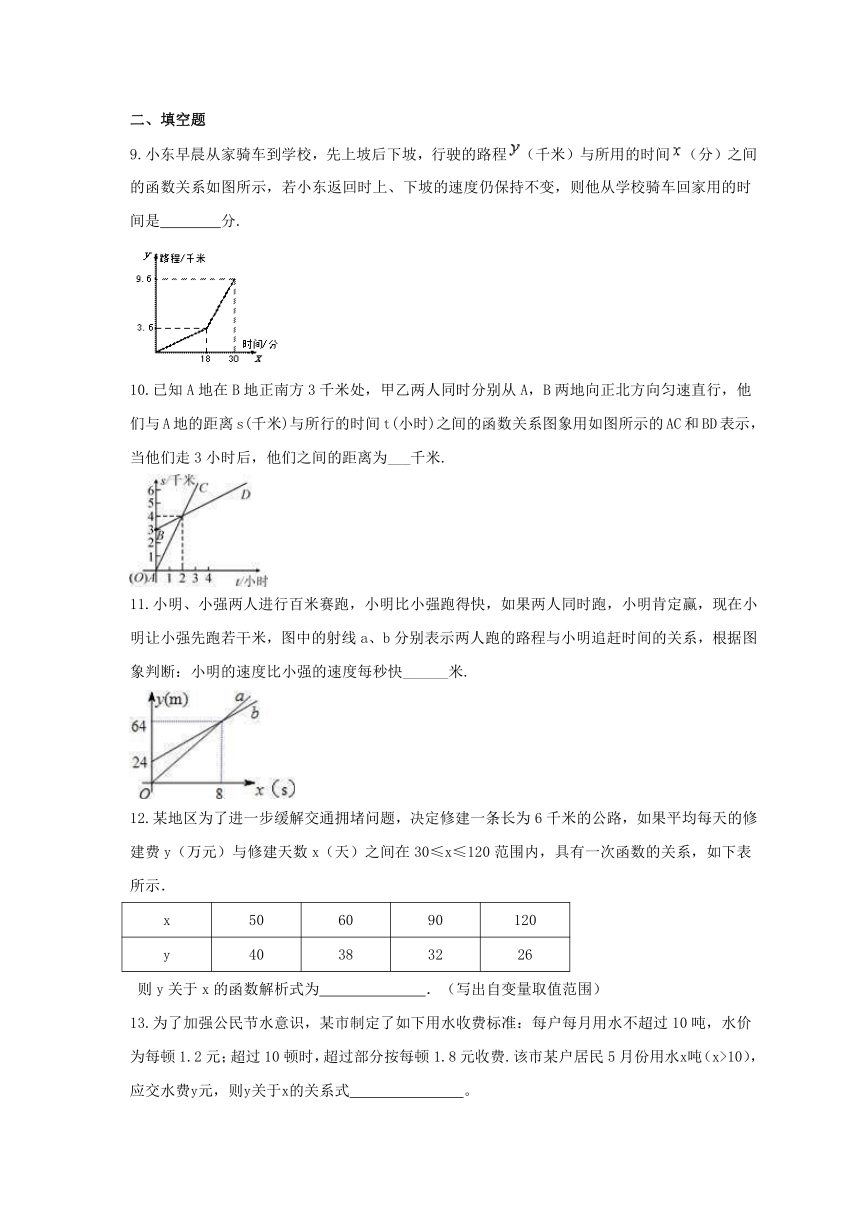

文档简介
2022年湘教版数学八年级下册
4.5《一次函数的应用》课时练习
一、选择题
1.某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
A.0.71元 B.2.3元 C.1.75元 D.1.4元
2.一辆慢车以50千米/小时的速度从甲地驶往乙地,一辆快车以75千米/小时的速度从乙地驶往甲地,甲、乙两地之间的距离为500千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与慢车行驶时间t(小时)之间的函数图象是( )
3.某种型号的计算器单价为40元,商家为了扩大销售量,现按八折销售,如果卖出x台这种计算器,共卖得y元,则用x表示y的关系式为( )
A.y=40x B.y=32x C.y=8x D.y=48x
4.甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶,甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(km)与两车行驶的时间x(h)之间的函数图象如图所示,则A,B两地之间的距离为( )
A.150 km B.300 km C.350 km D.450 km
5.甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是( )
A.甲的速度是4km/h B.乙的速度是10km/h
C.乙比甲晚出发1h D.甲比乙晚到B地3h
6.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地.已知甲、乙两地相距180千米,货车的速度为60千米/小时,小汽车的速度为90千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )
7.小明从家骑车上学,先上坡到达A地后再下坡到达学校,所用的时间与路程如图所示.如果返回时,上、下坡的速度仍然保持不变,那么他从学校回到家需要的时间是( )
A. 8.6分钟 B. 9分钟 C. 12分钟 D.16分钟
8.某市政府决定实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图,则下列说法中错误的是( )
A.甲队每天挖100米
B.乙队开挖两天后,每天挖50米
C.甲队比乙队提前2天完成任务
D.当x=3时,甲、乙两队所挖管道长度相同
二、填空题
9.小东早晨从家骑车到学校,先上坡后下坡,行驶的路程(千米)与所用的时间(分)之间的函数关系如图所示,若小东返回时上、下坡的速度仍保持不变,则他从学校骑车回家用的时间是 分.
10.已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离s(千米)与所行的时间t(小时)之间的函数关系图象用如图所示的AC和BD表示,当他们走3小时后,他们之间的距离为___千米.
11.小明、小强两人进行百米赛跑,小明比小强跑得快,如果两人同时跑,小明肯定赢,现在小明让小强先跑若干米,图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系,根据图象判断:小明的速度比小强的速度每秒快______米.
12.某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路,如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120范围内,具有一次函数的关系,如下表所示.
x 50 60 90 120
y 40 38 32 26
则y关于x的函数解析式为 .(写出自变量取值范围)
13.为了加强公民节水意识,某市制定了如下用水收费标准:每户每月用水不超过10吨,水价为每顿1.2元;超过10顿时,超过部分按每顿1.8元收费.该市某户居民5月份用水x吨(x>10),应交水费y元,则y关于x的关系式 。
14.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示.
则下列说法中:
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③甲队比乙队提前3天完成任务;
④当x=2或6时,甲乙两队所挖管道长度都相差100米.
正确的有 .(在横线上填写正确的序号)
三、解答题
15.某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示.
(1)第20天的总用水量为多少米3?
(2)当x≥20时,求y与x之间的函数关系式.
(3)种植时间为多少天时,总用水量达到7000米3?
16.为了提高天然气使用效率,保障居民的本机用气需求,某地积极推进阶梯式气价改革,若一户居民的年用气量不超过300m3,价格为2.5元/m3,若年用气量超过300m3,超出部分的价格为3元/m3,
(1)根据题意,填写下表:
(2)设一户居民的年用气量为xm3,付款金额为y元,求y关于x的解析式;
(3)若某户居民一年使用天然气所付的金额为870元,求该户居民的年用气量.
17.某果园苹果丰收,首批采摘46吨,计划租用A,B两种型号的汽车共10辆,一次性运往外地销售.A、B两种型号的汽车的满载量和租车费用如下:
A型汽车 B型汽车
满载量(吨) 5 4
费用(元)/次 800 600
设租A型汽车x辆,总租车费用为y元.
(1)求y与x之间的函数关系式;
(2)总租车费用最少是多少元?并说明此时的租车方案.
18.海洋王国暑假期间推出了两套优惠方案:
①购买成人票两张以上(包括两张),则儿童票按6折出售;
②成人票和儿童票一律按8.5折出售,已知成人票是350元/张,儿童票是240元/张,张华准备暑假期间带家人到长隆海洋王国游玩,准备购买8张成人票和若干张儿童票.
(1)请分别写出两种优惠方案中,购买的总费用y(元)与儿童人数x(人)之间的函数关系式;
(2)对x的取值情况进行分析,说明选择哪种方案购票更省钱.
参考答案
1.D.
2.C.
3.B
4.D
5.C
6.C
7.C
8.D
9.答案为:37.2
10.答案为:1.5;
11.答案为:3.
12.答案为:y=﹣0.2x+50.
13.答案为:y=1.8x-6
14.答案为:①②④
15.解:
16.解:
17.解:(1)y与x之间的函数关系式为:y=800x+600(10﹣x)=200x+6000;
(2)由题意可得:5x+4(10﹣x)≥46,∴x≥6,
∵y=200x+6000,∴当x=6时,y有最小值=7200(元),
此时租车的方案为:A型车6辆,B型车4辆.
18.解:(1)当选择方案①时,y=350×8+0.6×240x=144x+2800
当选择方案②时,y=(350×8+240)x×0.85=204x+2380
(2)当方案①费用高于方案②时
144x+2800>204x+2380,解得x<7
当方案①费用等于方案②时
144x+2800=204x+2380,解得x=7
当方案①费用低于方案②时
144x+2800<204x+2380,解得x>7
故当0<x<7时,选择方案②
当x=7时,两种方案费用一样.
当x>7时,选择方案①
4.5《一次函数的应用》课时练习
一、选择题
1.某市乘出租车需付车费y(元)与行车里程x(千米)之间函数关系的图象如图所示,那么该市乘出租车超过3千米后,每千米的费用是( )
A.0.71元 B.2.3元 C.1.75元 D.1.4元
2.一辆慢车以50千米/小时的速度从甲地驶往乙地,一辆快车以75千米/小时的速度从乙地驶往甲地,甲、乙两地之间的距离为500千米,两车同时出发,则图中折线大致表示两车之间的距离y(千米)与慢车行驶时间t(小时)之间的函数图象是( )
3.某种型号的计算器单价为40元,商家为了扩大销售量,现按八折销售,如果卖出x台这种计算器,共卖得y元,则用x表示y的关系式为( )
A.y=40x B.y=32x C.y=8x D.y=48x
4.甲、乙两车同时从A地出发,以各自的速度匀速向B地行驶,甲车先到达B地后,立即按原路以相同速度匀速返回(停留时间不作考虑),直到两车相遇.若甲、乙两车之间的距离y(km)与两车行驶的时间x(h)之间的函数图象如图所示,则A,B两地之间的距离为( )
A.150 km B.300 km C.350 km D.450 km
5.甲、乙两人沿相同的路线由A地到B地匀速前进,A、B两地间的路程为20km.他们前进的路程为s(km),甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息,下列说法正确的是( )
A.甲的速度是4km/h B.乙的速度是10km/h
C.乙比甲晚出发1h D.甲比乙晚到B地3h
6.货车和小汽车同时从甲地出发,以各自的速度匀速向乙地行驶,小汽车到达乙地后,立即以相同的速度沿原路返回甲地.已知甲、乙两地相距180千米,货车的速度为60千米/小时,小汽车的速度为90千米/小时,则下图中能分别反映出货车、小汽车离乙地的距离y(千米)与各自行驶时间t(小时)之间的函数图象是( )
7.小明从家骑车上学,先上坡到达A地后再下坡到达学校,所用的时间与路程如图所示.如果返回时,上、下坡的速度仍然保持不变,那么他从学校回到家需要的时间是( )
A. 8.6分钟 B. 9分钟 C. 12分钟 D.16分钟
8.某市政府决定实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图,则下列说法中错误的是( )
A.甲队每天挖100米
B.乙队开挖两天后,每天挖50米
C.甲队比乙队提前2天完成任务
D.当x=3时,甲、乙两队所挖管道长度相同
二、填空题
9.小东早晨从家骑车到学校,先上坡后下坡,行驶的路程(千米)与所用的时间(分)之间的函数关系如图所示,若小东返回时上、下坡的速度仍保持不变,则他从学校骑车回家用的时间是 分.
10.已知A地在B地正南方3千米处,甲乙两人同时分别从A,B两地向正北方向匀速直行,他们与A地的距离s(千米)与所行的时间t(小时)之间的函数关系图象用如图所示的AC和BD表示,当他们走3小时后,他们之间的距离为___千米.
11.小明、小强两人进行百米赛跑,小明比小强跑得快,如果两人同时跑,小明肯定赢,现在小明让小强先跑若干米,图中的射线a、b分别表示两人跑的路程与小明追赶时间的关系,根据图象判断:小明的速度比小强的速度每秒快______米.
12.某地区为了进一步缓解交通拥堵问题,决定修建一条长为6千米的公路,如果平均每天的修建费y(万元)与修建天数x(天)之间在30≤x≤120范围内,具有一次函数的关系,如下表所示.
x 50 60 90 120
y 40 38 32 26
则y关于x的函数解析式为 .(写出自变量取值范围)
13.为了加强公民节水意识,某市制定了如下用水收费标准:每户每月用水不超过10吨,水价为每顿1.2元;超过10顿时,超过部分按每顿1.8元收费.该市某户居民5月份用水x吨(x>10),应交水费y元,则y关于x的关系式 。
14.甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示.
则下列说法中:
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③甲队比乙队提前3天完成任务;
④当x=2或6时,甲乙两队所挖管道长度都相差100米.
正确的有 .(在横线上填写正确的序号)
三、解答题
15.某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示.
(1)第20天的总用水量为多少米3?
(2)当x≥20时,求y与x之间的函数关系式.
(3)种植时间为多少天时,总用水量达到7000米3?
16.为了提高天然气使用效率,保障居民的本机用气需求,某地积极推进阶梯式气价改革,若一户居民的年用气量不超过300m3,价格为2.5元/m3,若年用气量超过300m3,超出部分的价格为3元/m3,
(1)根据题意,填写下表:
(2)设一户居民的年用气量为xm3,付款金额为y元,求y关于x的解析式;
(3)若某户居民一年使用天然气所付的金额为870元,求该户居民的年用气量.
17.某果园苹果丰收,首批采摘46吨,计划租用A,B两种型号的汽车共10辆,一次性运往外地销售.A、B两种型号的汽车的满载量和租车费用如下:
A型汽车 B型汽车
满载量(吨) 5 4
费用(元)/次 800 600
设租A型汽车x辆,总租车费用为y元.
(1)求y与x之间的函数关系式;
(2)总租车费用最少是多少元?并说明此时的租车方案.
18.海洋王国暑假期间推出了两套优惠方案:
①购买成人票两张以上(包括两张),则儿童票按6折出售;
②成人票和儿童票一律按8.5折出售,已知成人票是350元/张,儿童票是240元/张,张华准备暑假期间带家人到长隆海洋王国游玩,准备购买8张成人票和若干张儿童票.
(1)请分别写出两种优惠方案中,购买的总费用y(元)与儿童人数x(人)之间的函数关系式;
(2)对x的取值情况进行分析,说明选择哪种方案购票更省钱.
参考答案
1.D.
2.C.
3.B
4.D
5.C
6.C
7.C
8.D
9.答案为:37.2
10.答案为:1.5;
11.答案为:3.
12.答案为:y=﹣0.2x+50.
13.答案为:y=1.8x-6
14.答案为:①②④
15.解:
16.解:
17.解:(1)y与x之间的函数关系式为:y=800x+600(10﹣x)=200x+6000;
(2)由题意可得:5x+4(10﹣x)≥46,∴x≥6,
∵y=200x+6000,∴当x=6时,y有最小值=7200(元),
此时租车的方案为:A型车6辆,B型车4辆.
18.解:(1)当选择方案①时,y=350×8+0.6×240x=144x+2800
当选择方案②时,y=(350×8+240)x×0.85=204x+2380
(2)当方案①费用高于方案②时
144x+2800>204x+2380,解得x<7
当方案①费用等于方案②时
144x+2800=204x+2380,解得x=7
当方案①费用低于方案②时
144x+2800<204x+2380,解得x>7
故当0<x<7时,选择方案②
当x=7时,两种方案费用一样.
当x>7时,选择方案①
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
