2021-2022学年人教版数学九年级下册26.2实际问题与反比例函数(2)课件(22张)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册26.2实际问题与反比例函数(2)课件(22张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 990.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 23:54:01 | ||
图片预览





文档简介
(共22张PPT)
26.2 实际问题与反比例函数(2)
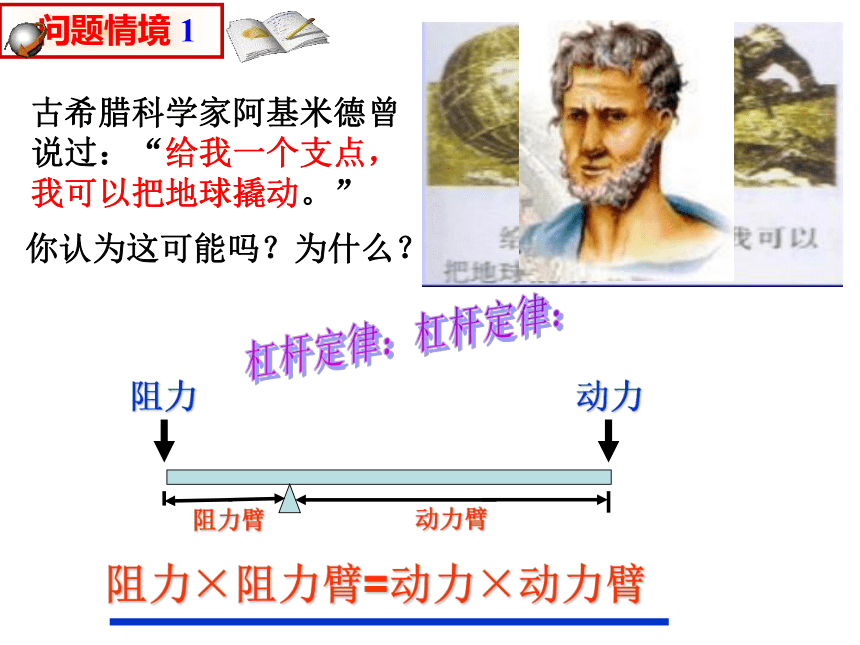
古希腊科学家阿基米德曾说过:“给我一个支点,我可以把地球撬动。”
你认为这可能吗?为什么?
阻力×阻力臂=动力×动力臂
阻力臂
阻力
动力
动力臂
问题情境 1
阻力
动力
阻力臂
动力臂
阻力×阻力臂=动力×动力臂
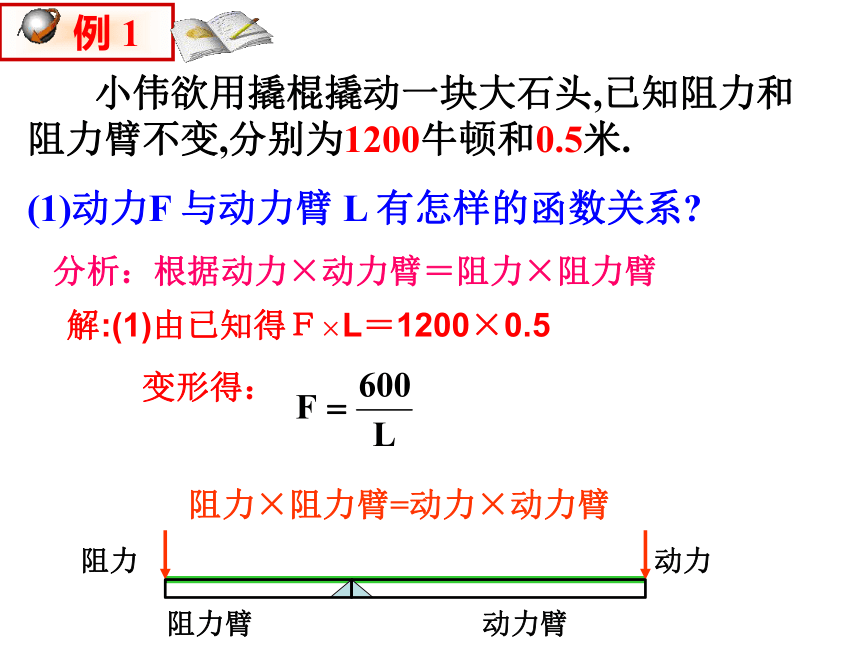
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛顿和0.5米.
(1)动力F 与动力臂 L 有怎样的函数关系
例 1
分析:根据动力×动力臂=阻力×阻力臂
解:(1)由已知得F×L=1200×0.5
变形得:
(2)小刚、小强、小健、小明分别选取了动力臂
为1米、1.5米、2米、3米的撬棍,你能得出
他们各自撬动石头至少需要多大的力吗?
从上述的运算中我们观察出什么规律?
解:(2)
发现:动力臂越长,用的力越小。
即动力臂越长就越省力
例 1.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛顿和0.5米.
阻力
动力
阻力臂
动力臂
阻力×阻力臂=动力×动力臂
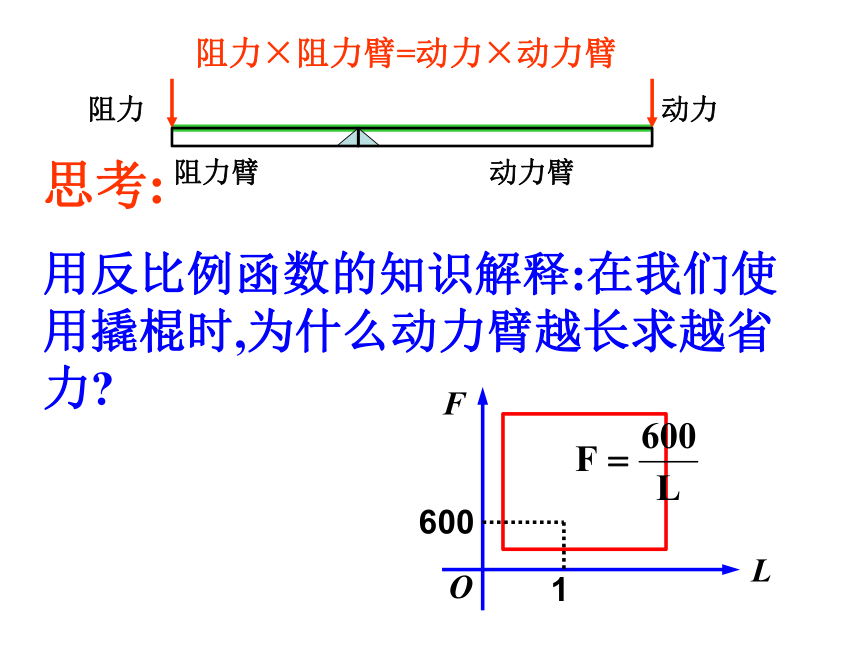
思考:
用反比例函数的知识解释:在我们使用撬棍时,为什么动力臂越长求越省力
F
600
O
1
L
思考:假定地球重量的近似值为6×1025牛顿
即为阻力),假设阿基米德有500牛顿的力量,
阻力臂为2000千米,请你帮助阿基米德设计
该用多长动力臂的杠杆才能把地球撬动.
解:(4)由已知得F×L=6×1025×2×103=1.2×1029
变形得:
当F=500时,L=2.4×1026千米
这个关系也可写为
P= ;或R=
问题情境 2
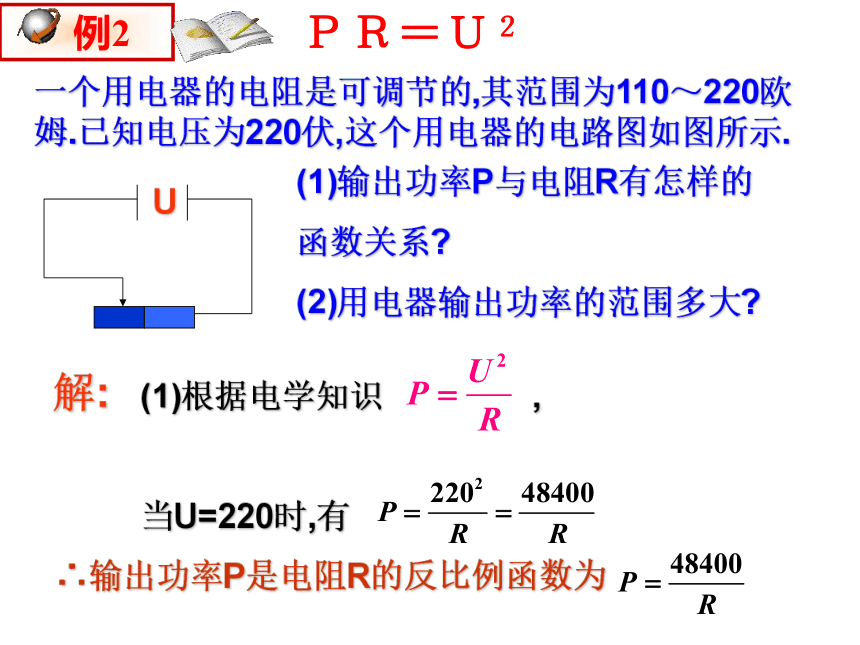
在电学知识中,用电器的输出功率P(瓦),两端的电压U(伏)及用电器的电阻R(欧姆)有如下关系:
PR=U2
一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.
U
(1)输出功率P与电阻R有怎样的
函数关系
(2)用电器输出功率的范围多大
解:
(1)根据电学知识 ,
当U=220时,有
∴输出功率P是电阻R的反比例函数为
例2
PR=U2
一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.
U
(1)输出功率P与电阻R有怎样的
函数关系
(2)用电器输出功率的范围多大
解(2)从(1)式可以看出,电阻越大则功率越小.
把电阻的最大值R=220代入①式,则得到输出功率的最小值
因此,用电器的输出功率在220瓦到440瓦之间.
把电阻的最小值R=110代入(1)式,得到输出功率最大值:
思考
结合上例,想一想为什么收音机音量、台灯的亮度以及电风扇的转速可以调节?
收音机的音量、台灯的亮度以及电风扇的转速是由用电器的输出功率决定的,通过调整输出功率的大小,就能调节收音机的音量、台灯的亮度以及电风扇的转速。
1、蓄电池的电压为定值.使用此电源时,电流I(A)与电R(Ω)之间的函数关系如图所示:
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
【解析】(1)由题意设函数表达式为
∵A(9,4)在图象上,
∴U=IR=36.
∴表达式为I= .
即蓄电池的电压是36伏.
反馈:
3
4
5
6
7
8
9
10
(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?
【解析】当I≤10A时,解得R≥3.6(Ω).所以可变电阻应不小于3.6Ω.
12 9 7.2 6 4.5 4 3.6
R
如图,为了预防“非典”,某学校对教室采用药熏消毒法进行消毒。
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例.
现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,求y与x的关系式;
(2)药物燃烧完后,求y与x的关系式;
(3)研究表明,当空气中每立方米的含药量低于1.6 mg时学生方可进入教室,那么从消毒开始,至少经过多少min后,学生才能回到教室;
(4)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?请说明理由。
例 3
如图,为了预防“非典”,某学校对教室采用药熏消毒法进行消毒。
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例.
(1)药物燃烧时,求y与x的关系式;
(2)药物燃烧完后,求y与x的关系式;
解:(1)当0≤x≤8时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
当x≥8时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
例 3
( 0≤x≤8)
(x≥8)
3
(4)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?请说明理由。
(4)把y=3代入两函数得
4
16
∴持续时间=16-4=12(min)>10(min)
答:此次消毒有效。
例 3
1、制作一种产品,需先将材料加热,达到60℃后,再进行操作,据了解,该材料加热时,温度y℃与时间x(min)成一次函数关系;停止加热进行操作时,温度y℃与时间x(min)成反比例关系,如图所示,已知该材料在操作加工前的温度为15℃,加热5min后温度达到60 ℃。
x
y
10
5
10
60
50
40
30
20
15
25
20
(1)分别求出将材料加热和停止加热进行操作时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于15 ℃时,必须停止操作,那么从开始加热到停止操作,共经历了多少时间?
( 0≤x≤5)
(x>5)
20min
反馈:
在直角坐标平面内,函数 (x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB.
(1)若⊿ABD的面积为4,求点B的坐标;
(2)求直线AB的函数解析式.
x
y
A
B
C
D
O
例4、
巩固训练
1、在某一电路中,保持电压不变,电流I(安培)和电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流I=2安培.
(1)求I与R之间的函数关系式;
(2)当电流I=0.5时,求电阻R的值.
2、一定质量的氧气,它的密度ρ (kg/m3)是它的体积V( m3) 的反比例函数, 当V=10m3时,ρ=1.43kg/m3.
(1)求ρ与V的函数关系式;
(2)求当V=2m3时求氧气的密度ρ.
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
26.2 实际问题与反比例函数(2)
古希腊科学家阿基米德曾说过:“给我一个支点,我可以把地球撬动。”
你认为这可能吗?为什么?
阻力×阻力臂=动力×动力臂
阻力臂
阻力
动力
动力臂
问题情境 1
阻力
动力
阻力臂
动力臂
阻力×阻力臂=动力×动力臂
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛顿和0.5米.
(1)动力F 与动力臂 L 有怎样的函数关系
例 1
分析:根据动力×动力臂=阻力×阻力臂
解:(1)由已知得F×L=1200×0.5
变形得:
(2)小刚、小强、小健、小明分别选取了动力臂
为1米、1.5米、2米、3米的撬棍,你能得出
他们各自撬动石头至少需要多大的力吗?
从上述的运算中我们观察出什么规律?
解:(2)
发现:动力臂越长,用的力越小。
即动力臂越长就越省力
例 1.小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂不变,分别为1200牛顿和0.5米.
阻力
动力
阻力臂
动力臂
阻力×阻力臂=动力×动力臂
思考:
用反比例函数的知识解释:在我们使用撬棍时,为什么动力臂越长求越省力
F
600
O
1
L
思考:假定地球重量的近似值为6×1025牛顿
即为阻力),假设阿基米德有500牛顿的力量,
阻力臂为2000千米,请你帮助阿基米德设计
该用多长动力臂的杠杆才能把地球撬动.
解:(4)由已知得F×L=6×1025×2×103=1.2×1029
变形得:
当F=500时,L=2.4×1026千米
这个关系也可写为
P= ;或R=
问题情境 2
在电学知识中,用电器的输出功率P(瓦),两端的电压U(伏)及用电器的电阻R(欧姆)有如下关系:
PR=U2
一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.
U
(1)输出功率P与电阻R有怎样的
函数关系
(2)用电器输出功率的范围多大
解:
(1)根据电学知识 ,
当U=220时,有
∴输出功率P是电阻R的反比例函数为
例2
PR=U2
一个用电器的电阻是可调节的,其范围为110~220欧姆.已知电压为220伏,这个用电器的电路图如图所示.
U
(1)输出功率P与电阻R有怎样的
函数关系
(2)用电器输出功率的范围多大
解(2)从(1)式可以看出,电阻越大则功率越小.
把电阻的最大值R=220代入①式,则得到输出功率的最小值
因此,用电器的输出功率在220瓦到440瓦之间.
把电阻的最小值R=110代入(1)式,得到输出功率最大值:
思考
结合上例,想一想为什么收音机音量、台灯的亮度以及电风扇的转速可以调节?
收音机的音量、台灯的亮度以及电风扇的转速是由用电器的输出功率决定的,通过调整输出功率的大小,就能调节收音机的音量、台灯的亮度以及电风扇的转速。
1、蓄电池的电压为定值.使用此电源时,电流I(A)与电R(Ω)之间的函数关系如图所示:
(1)蓄电池的电压是多少?你能写出这一函数的表达式吗?
【解析】(1)由题意设函数表达式为
∵A(9,4)在图象上,
∴U=IR=36.
∴表达式为I= .
即蓄电池的电压是36伏.
反馈:
3
4
5
6
7
8
9
10
(2)完成下表,并回答问题:如果以此蓄电池为电源的用电器限制电流不得超过10A,那么用电器的可变电阻应控制在什么范围内?
【解析】当I≤10A时,解得R≥3.6(Ω).所以可变电阻应不小于3.6Ω.
12 9 7.2 6 4.5 4 3.6
R
如图,为了预防“非典”,某学校对教室采用药熏消毒法进行消毒。
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例.
现测得药物8min燃毕,此时室内空气中每立方米的含药量为6mg。请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时,求y与x的关系式;
(2)药物燃烧完后,求y与x的关系式;
(3)研究表明,当空气中每立方米的含药量低于1.6 mg时学生方可进入教室,那么从消毒开始,至少经过多少min后,学生才能回到教室;
(4)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?请说明理由。
例 3
如图,为了预防“非典”,某学校对教室采用药熏消毒法进行消毒。
已知药物燃烧时,室内每立方米空气中的含药量y(mg)与时间x(min)成正比例,药物燃烧完后,y与x成反比例.
(1)药物燃烧时,求y与x的关系式;
(2)药物燃烧完后,求y与x的关系式;
解:(1)当0≤x≤8时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
当x≥8时设函数式为
∵函数图象经过点(8,6)
∴把(8,6)代入得
∴
例 3
( 0≤x≤8)
(x≥8)
3
(4)研究表明,当空气中每立方米的含药量不低于3mg且持续时间不低于10 min时,才能有效杀灭空气中的病菌,那么此次消毒是否有效?请说明理由。
(4)把y=3代入两函数得
4
16
∴持续时间=16-4=12(min)>10(min)
答:此次消毒有效。
例 3
1、制作一种产品,需先将材料加热,达到60℃后,再进行操作,据了解,该材料加热时,温度y℃与时间x(min)成一次函数关系;停止加热进行操作时,温度y℃与时间x(min)成反比例关系,如图所示,已知该材料在操作加工前的温度为15℃,加热5min后温度达到60 ℃。
x
y
10
5
10
60
50
40
30
20
15
25
20
(1)分别求出将材料加热和停止加热进行操作时y与x的函数关系式;
(2)根据工艺要求,当材料温度低于15 ℃时,必须停止操作,那么从开始加热到停止操作,共经历了多少时间?
( 0≤x≤5)
(x>5)
20min
反馈:
在直角坐标平面内,函数 (x>0,m是常数)的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD,DC,CB.
(1)若⊿ABD的面积为4,求点B的坐标;
(2)求直线AB的函数解析式.
x
y
A
B
C
D
O
例4、
巩固训练
1、在某一电路中,保持电压不变,电流I(安培)和电阻R(欧姆)成反比例,当电阻R=5欧姆时,电流I=2安培.
(1)求I与R之间的函数关系式;
(2)当电流I=0.5时,求电阻R的值.
2、一定质量的氧气,它的密度ρ (kg/m3)是它的体积V( m3) 的反比例函数, 当V=10m3时,ρ=1.43kg/m3.
(1)求ρ与V的函数关系式;
(2)求当V=2m3时求氧气的密度ρ.
x(cm) … 10 15 20 25 30 …
y(N) … 30 20 15 12 10 …
