2021-2022学年人教版数学九年级下册第27章相似三角形的复习课件(32张)
文档属性
| 名称 | 2021-2022学年人教版数学九年级下册第27章相似三角形的复习课件(32张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 993.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-07 00:00:00 | ||
图片预览








文档简介
(共32张PPT)
课前热身:
1、根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(1) ∠A=120°,AB=7 ,AC=14 ∠A′=120°,A′B′=3 ,A′C′=6
(2) AB=4 ,BC=6, AC=8; A′B′=12,B′C′=18 ,A′C′=21
(3) ∠A=70°,∠B=48°, ∠A′=70°, ∠C′=62°
2、在△ABC中,DE∥BC,若AD:DB=1:3,DE=2,则BC的长为( )
B
C
E
D
A
课前热身:
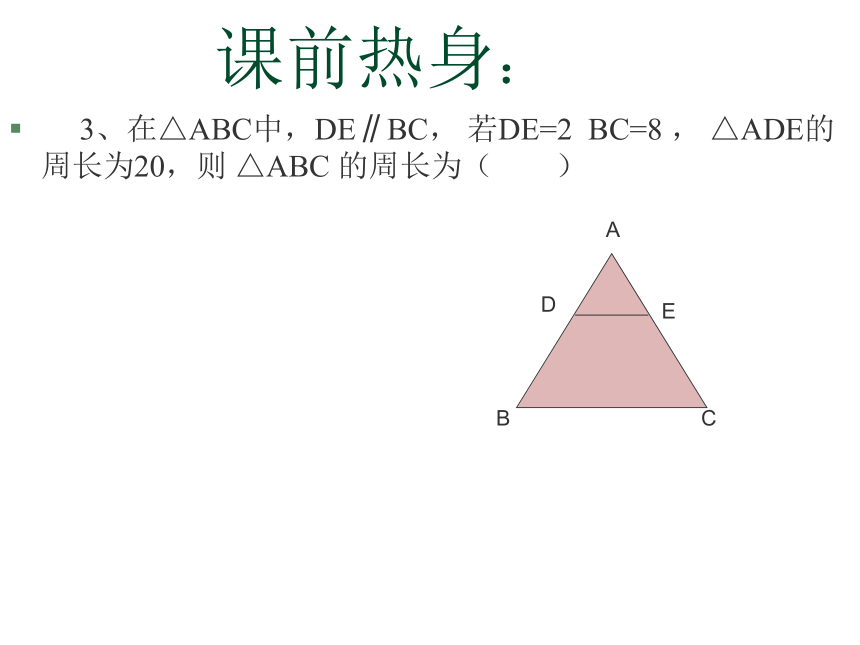
3、在△ABC中,DE∥BC, 若DE=2 BC=8 , △ADE的周长为20,则 △ABC 的周长为( )
B
C
E
D
A
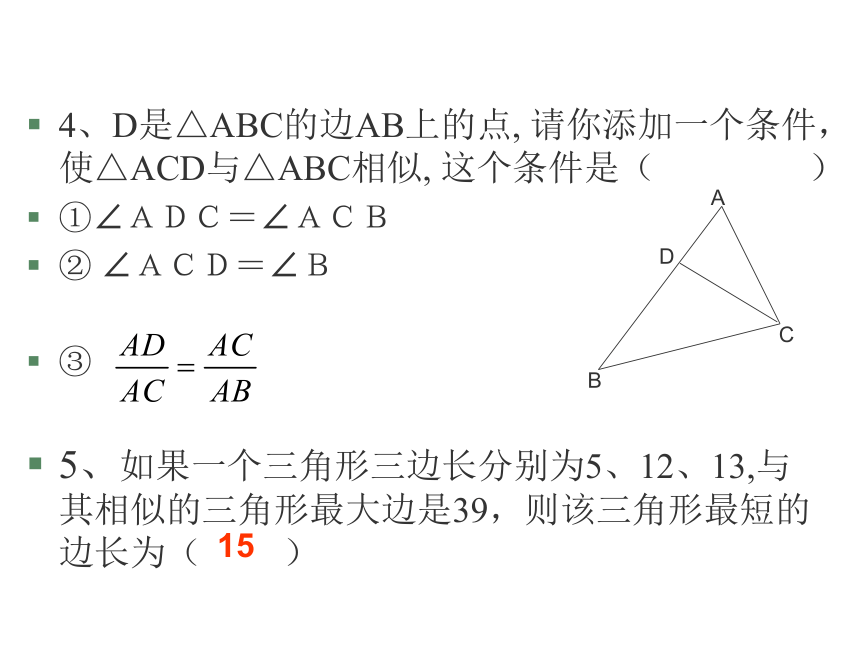
4、D是△ABC的边AB上的点, 请你添加一个条件,使△ACD与△ABC相似, 这个条件是( )
①∠ADC=∠ACB
② ∠ACD=∠B
③
5、如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为( )
A
D
C
B
15
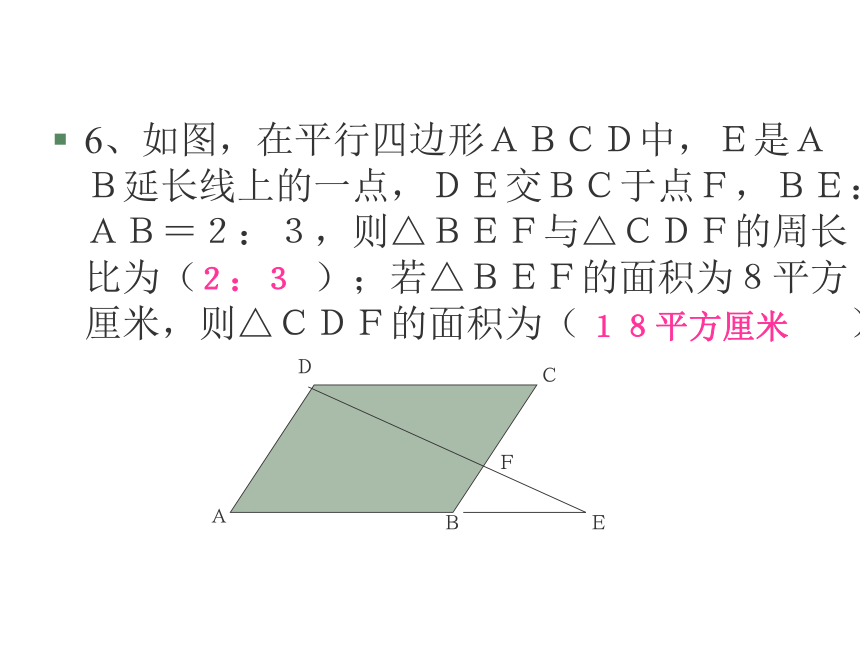
6、如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F,BE:AB=2:3,则△BEF与△CDF的周长比为( );若△BEF的面积为8平方厘米,则△CDF的面积为( )
2:3
18平方厘米
A
B
E
C
D
F
A
B
C
D
E
F
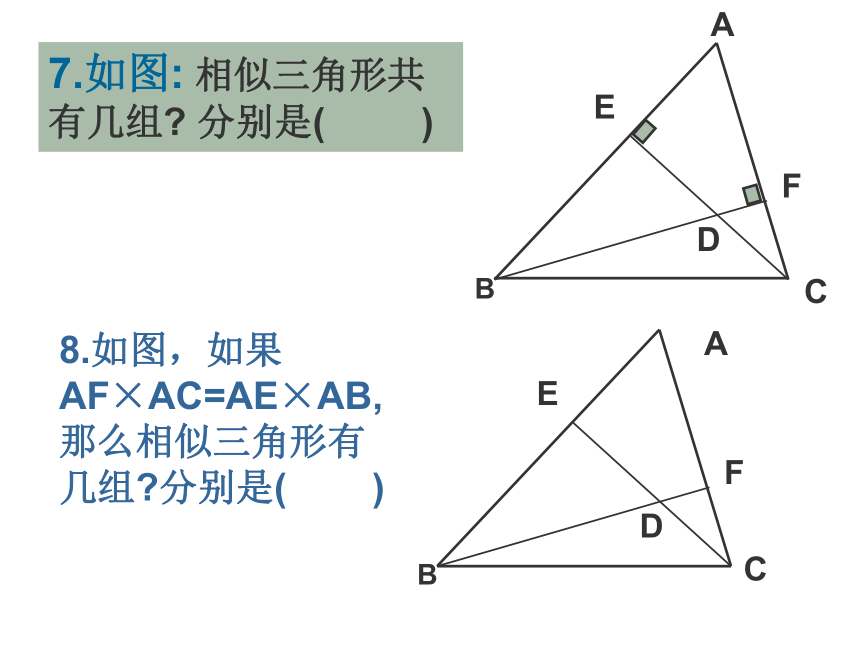
7.如图: 相似三角形共有几组 分别是( )
B
C
D
E
F
A
8.如图,如果AF×AC=AE×AB,那么相似三角形有几组 分别是( )
1. 成比例的项:
叫做成比例的项。
那么
或
若
,
:
:
c
b
a
d
d
c
b
a
d
c
b
a
=
=
,
,
,
其中 :a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
若 四条线段 a、b、c、d 中,如果
(或a:b=c:d),那么这四条线段a、b、 c 、 d
叫做成比例的线段,简称比例线段.
a c
b d
=
比例的性质:
bc
ad
d
c
b
a
=
=
;
1.若a, b, c, d成比例,且a=2, b=3, c=4,那么d=
6
2、下列各组线段的长度成比例的是( )
A. 2 , 3, 4, 1 B. 1.5 ,2.5 ,6.5 , 4.5
C. 1.1 ,2.2 ,3.3 ,4.4 D. 1 , 2 , 2 , 4
m
n
m
=
n
5
6
已知 ,求 的值.
解:方法(1)由对调比例式的两内项比例式仍成立得:
m
n
6
5
=
方法(2)因为 ,所以5m=6n
m
6
n
5
=
6
m
n
=
所以
5
3、
4、已知 1) x:(x+1)=(1—x):3,求x。
(2)若 , 求 。
(3) 若 ,求 ,
.
=
-
2x
3y
+
y
x
1
2
y
x
a+b
b
=
6
5
a
b
a-b
b
5
6 已知1, 2, 3三个数,请你再添上一个数,写出一个比例式。
2.比例中项:
当两个比例内项相等时,
即
a b
b c
= ,
(或 a:b=b:c),
那么线段 b 叫做线段 a 和 c 的比例中项.
2
ac
b
=
即:
3.黄金分割:
A
C
B
4
1.相似三角形的定义:
对应角相等、对应边成比例的三角形叫做相似三角形。
2.相似比:
相似三角形的对应边的比,叫做相似三角形的相似比。
△ABC∽△A/B/C/,如果BC=3,B/C/=1.5,那么△A/B/C/与
△ABC的相似比为_________.
3.相似三角形的判定
(1)通过平行线。
(2)三边对应成比例.
(3)两边对应成比例且夹角相等 。
(4)两角相等。
4.相似三角形的性质
(1)对应边的比相等,对应角相等
(2)相似三角形的周长比等于相似比
(3)相似三角形的面积比等于相似比的平方
(4)相似三角形的对应边上的高、中线、角 平分线的比等于相似比
5.相似三角形的应用:
1、利用三角形相似,可证明角相等;线段成比例(或等积式);
2、利用三角形相似,求线段的长等
3、利用三角形相似,可以解决一些不能直接测量的物体的长度。如求河的宽度、求建筑物的高度等。
例1、如图,△ABC∽△A`B`C`,它们的周长分别为60cm和72cm,且AB=15cm,B`C`=24cm,
求BC、AC、A`B` 、 A`C`的长。
A
B
C
A`
B`
C`
证明:∵CD⊥AB, E为AC的中点
∴ DE=AE
∴∠EDA=∠A
∵ ∠EDA=∠FDB
∴∠A=∠FDB
∵∠ACB= Rt ∠
∴ ∠A=∠FCD
∴ ∠FDB=∠FCD
∵ △FDB∽△FCD
∴ BD:CD=DF:CF
∴ BD·CF=CD·DF
例2、 如图,CD是Rt△ABC斜边上的高,E为AC的中点,
ED交CB的延长线于F。
C
E
A
D
F
B
求证:BD·CF=CD·DF
例3、 过 ABC的顶点C任作一直线,与边AB及中线AD分别交于点F和E,
求证:AE:ED=2AF:FB。
C
A
B
F
D
E
二.知识应用:
1.找一找:
(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.
(2) 如图2,已知:△ABC中, ∠ACB=Rt∠ ,CD⊥ AB于D,DE⊥BC于E,则图中共有_____个三角形和△ABC相似.
A
B
C
D
E
F
如图(1)
3
E
A
B
C
D
如图(2)
4
(3)如图3,∠1= ∠2= ∠3,则图中相似三角形的组数为
________.
A
D
B
E
C
1
3
2
如图(3)
4
(4)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,则图中共有_____对三角形相似.
·
A
B
C
D
E
O
(5)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,且AC平分∠BAD,则图中共有_____对三角形相似.
·
A
B
C
D
E
O
1
2
3
4
6
2
2.画一画:
如图,在△ABC和△DEF中, ∠A=∠D=700, ∠B=500, ∠E=300,画直线a,把△ABC分成两个三角形,画直线b ,把△DEF分成两个三角形,使△ABC分成的两个三角形和△DEF分成的两个三角形分别相似.(要求标注数据)
300
300
C
A
B
700
500
E
D
F
700
300
a
b
C
A
B
700
500
E
D
F
700
300
a
b
200
200
3.已知,如图,梯形ABCD中,AD∥BC, ∠A=900,对角线BD⊥CD
求证:(1) △ABD∽△DCB;
(2)BD2=AD·BC
A
B
C
D
4.如图,P是△ABC中AB边上的一点,要使△ACP和△ABC相似,则需添加一个条件:_____________________________________
。
A
B
C
P
∠ACP=∠B;
或∠APC=∠ACB;
或AP:AC=AC:AB即AC2=AP·AB
如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足什么关系时, △ACP∽ △PDB.
(2)当△ACP∽ △PDB时,求∠APB的度数.
5.想一想:
A
B
C
D
P
6.练一练:
将两块完全相同的等腰直角三角形摆放成如图所示的样子,假设图形中的所有点,线都在同一平面内,试写出一对相似三角形(不全等)______________.
G
A
B
C
D
E
F
1
7.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE的形状相同。
E
A
B
C
D
M
N
8.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
·P
9.已知:如图, ∠ACB=90°,AD=DB,DE⊥AB于D交AC于E,交BC的延长线于F,试说明: DC2=DE·DF
利用相似三角形的性质
A
D
B
F
C
E
10.已知,如图,CE是直角△ABC的斜边AB上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP,垂足为G,交CE于D, 试说明:CE2=ED·EP.
利用等积式代换
P
G
A
B
E
C
D
.如图, △ABC中,AB=6,BC=4,AC=3,点P在BC上运动,过P点作∠DPB=∠A,PD交AB于D,设PB=x,AD=y.
(1)求y关于x的函数关系式和x的取值范围.
(2)当x取何值时,y最小,最小值是多少
11.思考题:
P
A
B
C
D
P
B
A
C
D
E
F
M
N
B
A
C
D
E
F
图一
图二
课外拓展:
右图中,在一直角三角形余料中截出一个面积最大的正方形零件,应如何截取? (设三角形的三边分别是3、4、5、那么最大的面积是多少?)
B
A
C
课前热身:
1、根据下列条件能否判定△ABC与△A′B′C′相似?为什么?
(1) ∠A=120°,AB=7 ,AC=14 ∠A′=120°,A′B′=3 ,A′C′=6
(2) AB=4 ,BC=6, AC=8; A′B′=12,B′C′=18 ,A′C′=21
(3) ∠A=70°,∠B=48°, ∠A′=70°, ∠C′=62°
2、在△ABC中,DE∥BC,若AD:DB=1:3,DE=2,则BC的长为( )
B
C
E
D
A
课前热身:
3、在△ABC中,DE∥BC, 若DE=2 BC=8 , △ADE的周长为20,则 △ABC 的周长为( )
B
C
E
D
A
4、D是△ABC的边AB上的点, 请你添加一个条件,使△ACD与△ABC相似, 这个条件是( )
①∠ADC=∠ACB
② ∠ACD=∠B
③
5、如果一个三角形三边长分别为5、12、13,与其相似的三角形最大边是39,则该三角形最短的边长为( )
A
D
C
B
15
6、如图,在平行四边形ABCD中,E是AB延长线上的一点,DE交BC于点F,BE:AB=2:3,则△BEF与△CDF的周长比为( );若△BEF的面积为8平方厘米,则△CDF的面积为( )
2:3
18平方厘米
A
B
E
C
D
F
A
B
C
D
E
F
7.如图: 相似三角形共有几组 分别是( )
B
C
D
E
F
A
8.如图,如果AF×AC=AE×AB,那么相似三角形有几组 分别是( )
1. 成比例的项:
叫做成比例的项。
那么
或
若
,
:
:
c
b
a
d
d
c
b
a
d
c
b
a
=
=
,
,
,
其中 :a、b、c、d 叫做组成比例的项,
线段 a、d 叫做比例外项,
线段 b、c 叫做比例内项,
若 四条线段 a、b、c、d 中,如果
(或a:b=c:d),那么这四条线段a、b、 c 、 d
叫做成比例的线段,简称比例线段.
a c
b d
=
比例的性质:
bc
ad
d
c
b
a
=
=
;
1.若a, b, c, d成比例,且a=2, b=3, c=4,那么d=
6
2、下列各组线段的长度成比例的是( )
A. 2 , 3, 4, 1 B. 1.5 ,2.5 ,6.5 , 4.5
C. 1.1 ,2.2 ,3.3 ,4.4 D. 1 , 2 , 2 , 4
m
n
m
=
n
5
6
已知 ,求 的值.
解:方法(1)由对调比例式的两内项比例式仍成立得:
m
n
6
5
=
方法(2)因为 ,所以5m=6n
m
6
n
5
=
6
m
n
=
所以
5
3、
4、已知 1) x:(x+1)=(1—x):3,求x。
(2)若 , 求 。
(3) 若 ,求 ,
.
=
-
2x
3y
+
y
x
1
2
y
x
a+b
b
=
6
5
a
b
a-b
b
5
6 已知1, 2, 3三个数,请你再添上一个数,写出一个比例式。
2.比例中项:
当两个比例内项相等时,
即
a b
b c
= ,
(或 a:b=b:c),
那么线段 b 叫做线段 a 和 c 的比例中项.
2
ac
b
=
即:
3.黄金分割:
A
C
B
4
1.相似三角形的定义:
对应角相等、对应边成比例的三角形叫做相似三角形。
2.相似比:
相似三角形的对应边的比,叫做相似三角形的相似比。
△ABC∽△A/B/C/,如果BC=3,B/C/=1.5,那么△A/B/C/与
△ABC的相似比为_________.
3.相似三角形的判定
(1)通过平行线。
(2)三边对应成比例.
(3)两边对应成比例且夹角相等 。
(4)两角相等。
4.相似三角形的性质
(1)对应边的比相等,对应角相等
(2)相似三角形的周长比等于相似比
(3)相似三角形的面积比等于相似比的平方
(4)相似三角形的对应边上的高、中线、角 平分线的比等于相似比
5.相似三角形的应用:
1、利用三角形相似,可证明角相等;线段成比例(或等积式);
2、利用三角形相似,求线段的长等
3、利用三角形相似,可以解决一些不能直接测量的物体的长度。如求河的宽度、求建筑物的高度等。
例1、如图,△ABC∽△A`B`C`,它们的周长分别为60cm和72cm,且AB=15cm,B`C`=24cm,
求BC、AC、A`B` 、 A`C`的长。
A
B
C
A`
B`
C`
证明:∵CD⊥AB, E为AC的中点
∴ DE=AE
∴∠EDA=∠A
∵ ∠EDA=∠FDB
∴∠A=∠FDB
∵∠ACB= Rt ∠
∴ ∠A=∠FCD
∴ ∠FDB=∠FCD
∵ △FDB∽△FCD
∴ BD:CD=DF:CF
∴ BD·CF=CD·DF
例2、 如图,CD是Rt△ABC斜边上的高,E为AC的中点,
ED交CB的延长线于F。
C
E
A
D
F
B
求证:BD·CF=CD·DF
例3、 过 ABC的顶点C任作一直线,与边AB及中线AD分别交于点F和E,
求证:AE:ED=2AF:FB。
C
A
B
F
D
E
二.知识应用:
1.找一找:
(1) 如图1,已知:DE∥BC,EF ∥AB,则图中共有_____对三角形相似.
(2) 如图2,已知:△ABC中, ∠ACB=Rt∠ ,CD⊥ AB于D,DE⊥BC于E,则图中共有_____个三角形和△ABC相似.
A
B
C
D
E
F
如图(1)
3
E
A
B
C
D
如图(2)
4
(3)如图3,∠1= ∠2= ∠3,则图中相似三角形的组数为
________.
A
D
B
E
C
1
3
2
如图(3)
4
(4)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,则图中共有_____对三角形相似.
·
A
B
C
D
E
O
(5)已知:四边形ABCD内接于⊙O,连结AC和BD交于点E,且AC平分∠BAD,则图中共有_____对三角形相似.
·
A
B
C
D
E
O
1
2
3
4
6
2
2.画一画:
如图,在△ABC和△DEF中, ∠A=∠D=700, ∠B=500, ∠E=300,画直线a,把△ABC分成两个三角形,画直线b ,把△DEF分成两个三角形,使△ABC分成的两个三角形和△DEF分成的两个三角形分别相似.(要求标注数据)
300
300
C
A
B
700
500
E
D
F
700
300
a
b
C
A
B
700
500
E
D
F
700
300
a
b
200
200
3.已知,如图,梯形ABCD中,AD∥BC, ∠A=900,对角线BD⊥CD
求证:(1) △ABD∽△DCB;
(2)BD2=AD·BC
A
B
C
D
4.如图,P是△ABC中AB边上的一点,要使△ACP和△ABC相似,则需添加一个条件:_____________________________________
。
A
B
C
P
∠ACP=∠B;
或∠APC=∠ACB;
或AP:AC=AC:AB即AC2=AP·AB
如图,点C,D在线段AB上, △PCD是等边三角形.
(1)当AC,CD,DB满足什么关系时, △ACP∽ △PDB.
(2)当△ACP∽ △PDB时,求∠APB的度数.
5.想一想:
A
B
C
D
P
6.练一练:
将两块完全相同的等腰直角三角形摆放成如图所示的样子,假设图形中的所有点,线都在同一平面内,试写出一对相似三角形(不全等)______________.
G
A
B
C
D
E
F
1
7.如图,正方形ABCD的边长为8,E是AB的中点,点M,N分别在BC,CD上,且CM=2,则当CN=_________时,△CMN与△ADE的形状相同。
E
A
B
C
D
M
N
8.在平面直角坐标系,B(1,0), A(3,-3), C(3,0),点P在y轴的正半轴上运动,若以O,B,P为顶点的三角形与△ABC相似,则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
·P
9.已知:如图, ∠ACB=90°,AD=DB,DE⊥AB于D交AC于E,交BC的延长线于F,试说明: DC2=DE·DF
利用相似三角形的性质
A
D
B
F
C
E
10.已知,如图,CE是直角△ABC的斜边AB上的高,在EC的延长线上任取一点P,连接AP,作BG⊥AP,垂足为G,交CE于D, 试说明:CE2=ED·EP.
利用等积式代换
P
G
A
B
E
C
D
.如图, △ABC中,AB=6,BC=4,AC=3,点P在BC上运动,过P点作∠DPB=∠A,PD交AB于D,设PB=x,AD=y.
(1)求y关于x的函数关系式和x的取值范围.
(2)当x取何值时,y最小,最小值是多少
11.思考题:
P
A
B
C
D
P
B
A
C
D
E
F
M
N
B
A
C
D
E
F
图一
图二
课外拓展:
右图中,在一直角三角形余料中截出一个面积最大的正方形零件,应如何截取? (设三角形的三边分别是3、4、5、那么最大的面积是多少?)
B
A
C
