2021-2022学年北师大版九年级数学下册3.2圆的对称性课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.2圆的对称性课件(共16张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 13:34:01 | ||
图片预览






文档简介
(共16张PPT)
九年级下册
3.2 圆的对称性
学习目标
理解圆的轴对称性和中心对称性,会画出圆的对称轴,会找圆的对称。
掌握圆心角、弧和弦之间的关系,并会用它们之间的关系解题。
1
2
通过对圆心角、弧和弦之间的关系的探究,掌握解题的方法和技巧。
3
情景引入
请观察下列三个银行标志有何共同点
自主学习
圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
圆是中心对称图形吗?
如果是,它的对称中心是什么 你能找到多少个对称中心?
你又是用什么方法解决这个问题的
结论归纳
利用折叠的方法,我们可以得到
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
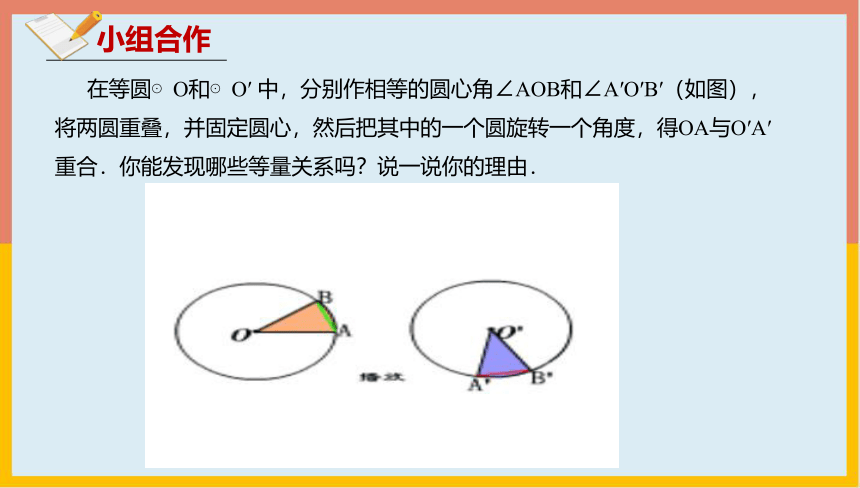
小组合作
在等圆⊙O和⊙O′ 中,分别作相等的圆心角∠AOB和∠A′O′B′(如图),将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,得OA与O′A′重合.你能发现哪些等量关系吗?说一说你的理由.
合作探究
小红认为AB=A'B',AB=A'B'.
解:∵ 半径OA与O'A'重合,∠AOB=∠A'O'B'
∴ 半径OB与O'B'重合
∵ 点A与点A'重合,点B与点B'重合
∴ AB与A'B'重合,弦AB与弦A'B'重合
∴ AB=A'B',AB=A'B'.
结论归纳
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?你是怎么想的?
如果弦相等呢?你能得出什么结论?
合作探究
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们对应的其余各组量都分别相等.
在同圆或等圆中,如果轮换下面五组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论 与同伴交流你的想法和理由.
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
拓展与深化
典例精析
例 如图,AB,DE是⊙O的直径,C是⊙O上一点,且AD=CE,BE与CE的大小有什么关系?为什么?
解:BE=CE。 理由是:
∵ ∠AOD=∠BOE
∴ BE=CE
∴ AD=CE
∴ BE=CE
典例精析
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E、F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系?AB与CD的大小有什么关系?为什么? ∠AOB与∠COD呢?
解:(1)如果∠AOB=∠COD
那么OE=OF. 理由是:
∵∠AOB=∠COD,∴AB=CD
∵OE⊥AB,OF⊥CD
∴AE= AB,CF= CD
∴AE=CF
又∵OA=OC
∴Rt△OAE≌Rt△OCF
∴OE=OF
(2)如果OE=OF,那么
AB=CD,AB=CD,∠AOB=∠COD
理由是:∵OA=OC,OE=OF
∴Rt△OAE≌Rt△OCF
∴AE=CF,
∵OE⊥AB,OF⊥CD
∴AE= AB,CF= CD
∴AB=2AE,CD=2CF,
∴AB=CD
∴AB=CD,∠AOB=∠COD
解析一览
随堂检测
1.在同圆或等圆中,相等的圆心角所对的___,相等,所对的___相等.
2.在同圆或等圆中,如果两个______,两条___,两条___中有一组量相等,那么它们所对应的其余各组量都分别相等.
3.一条弦把圆分成1:3两部分,则弦所对的圆心角为______.
4.弦心距是弦的一半时,弦与直径的比是_______,弦所对的圆心角是____.
5.如图,AB、CD是⊙O的
直径OE⊥AB,OF⊥CD,
则∠EOD____∠BOF,
AC___AE,AC___AE.
课堂小结
这节课你有何收获或困惑?说出来大家分享。
个性化作业
1.完成九年级下册3.2圆的对称性A组 课后作业。
2.预习课本垂径定理及推论,完成下一节自主学习检测题目。
A组
B组
九年级下册
3.2 圆的对称性
学习目标
理解圆的轴对称性和中心对称性,会画出圆的对称轴,会找圆的对称。
掌握圆心角、弧和弦之间的关系,并会用它们之间的关系解题。
1
2
通过对圆心角、弧和弦之间的关系的探究,掌握解题的方法和技巧。
3
情景引入
请观察下列三个银行标志有何共同点
自主学习
圆是轴对称图形吗?
如果是,它的对称轴是什么 你能找到多少条对称轴?
你是用什么方法解决上述问题的
圆是中心对称图形吗?
如果是,它的对称中心是什么 你能找到多少个对称中心?
你又是用什么方法解决这个问题的
结论归纳
利用折叠的方法,我们可以得到
圆是轴对称图形,其对称轴是任意一条过圆心的直线.
圆也是中心对称图形.
它的对称中心就是圆心.
用旋转的方法即可解决这个问题.
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.
小组合作
在等圆⊙O和⊙O′ 中,分别作相等的圆心角∠AOB和∠A′O′B′(如图),将两圆重叠,并固定圆心,然后把其中的一个圆旋转一个角度,得OA与O′A′重合.你能发现哪些等量关系吗?说一说你的理由.
合作探究
小红认为AB=A'B',AB=A'B'.
解:∵ 半径OA与O'A'重合,∠AOB=∠A'O'B'
∴ 半径OB与O'B'重合
∵ 点A与点A'重合,点B与点B'重合
∴ AB与A'B'重合,弦AB与弦A'B'重合
∴ AB=A'B',AB=A'B'.
结论归纳
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等.
在同圆或等圆中,如果两个圆心角所对的弧相等,那么它们所对的弦相等吗?这两个圆心角相等吗?你是怎么想的?
如果弦相等呢?你能得出什么结论?
合作探究
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们对应的其余各组量都分别相等.
在同圆或等圆中,如果轮换下面五组条件:
①两个圆心角,②两条弧,③两条弦,④两条弦心距,你能得出什么结论 与同伴交流你的想法和理由.
如由条件:
②AB=A′B′
⌒ ⌒
③AB=A′B′
④ OD=O′D′
可推出
①∠AOB=∠A′O′B′
拓展与深化
典例精析
例 如图,AB,DE是⊙O的直径,C是⊙O上一点,且AD=CE,BE与CE的大小有什么关系?为什么?
解:BE=CE。 理由是:
∵ ∠AOD=∠BOE
∴ BE=CE
∴ AD=CE
∴ BE=CE
典例精析
如图,在⊙O中,AB,CD是两条弦,OE⊥AB,OF⊥CD,垂足分别为E、F.
(1)如果∠AOB=∠COD,那么OE与OF的大小有什么关系?为什么?
(2)如果OE=OF,那么AB与CD的大小有什么关系?AB与CD的大小有什么关系?为什么? ∠AOB与∠COD呢?
解:(1)如果∠AOB=∠COD
那么OE=OF. 理由是:
∵∠AOB=∠COD,∴AB=CD
∵OE⊥AB,OF⊥CD
∴AE= AB,CF= CD
∴AE=CF
又∵OA=OC
∴Rt△OAE≌Rt△OCF
∴OE=OF
(2)如果OE=OF,那么
AB=CD,AB=CD,∠AOB=∠COD
理由是:∵OA=OC,OE=OF
∴Rt△OAE≌Rt△OCF
∴AE=CF,
∵OE⊥AB,OF⊥CD
∴AE= AB,CF= CD
∴AB=2AE,CD=2CF,
∴AB=CD
∴AB=CD,∠AOB=∠COD
解析一览
随堂检测
1.在同圆或等圆中,相等的圆心角所对的___,相等,所对的___相等.
2.在同圆或等圆中,如果两个______,两条___,两条___中有一组量相等,那么它们所对应的其余各组量都分别相等.
3.一条弦把圆分成1:3两部分,则弦所对的圆心角为______.
4.弦心距是弦的一半时,弦与直径的比是_______,弦所对的圆心角是____.
5.如图,AB、CD是⊙O的
直径OE⊥AB,OF⊥CD,
则∠EOD____∠BOF,
AC___AE,AC___AE.
课堂小结
这节课你有何收获或困惑?说出来大家分享。
个性化作业
1.完成九年级下册3.2圆的对称性A组 课后作业。
2.预习课本垂径定理及推论,完成下一节自主学习检测题目。
A组
B组
