1.7.1整式的除法(1) 课件(共21张PPT)
文档属性
| 名称 | 1.7.1整式的除法(1) 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 668.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 17:52:15 | ||
图片预览






文档简介
(共21张PPT)
1.7.1整式的除法(1)
第一章
整式的乘除
2021-2022学年七年级数学下册同步(北师大版)
学习目标
1.理解和掌握单项式除以单项式的运算法则,运用运
算法则熟练、准确地进行计算.
2.通过总结法则,培养概括能力;训练综合解题能力
和计算能力.
导入新课
木星的质量约是1.9×1024吨,地球的质量约是5.98×1021吨,你知道木星的质量约为地球质量的多少倍吗
木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.
想一想:上面的式子该如何计算
地球
木星
学习了今天的知识,我们就能解决这个问题了!
讲授新课
单项式除以单项式
你能计算下列各题吗?如果能,说说你的理由.
(1)x5y÷x2=;
(2)8m2n2÷2m2n=;
(3)a4b2c÷3a2b=.
除法
乘法
互逆运算
( ). x2 =x5y
( ).2m2n=8m2n2
( ). 3a2b=a4b2c
讲授新课
方法2:利用类似分数约分的方法
约分时,先约系数,再约同底数幂,分子中单独存在的字母及其指数直接作为商的因式.
单项式相除, 把系数、同底数幂分别相除作为商的因式;对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
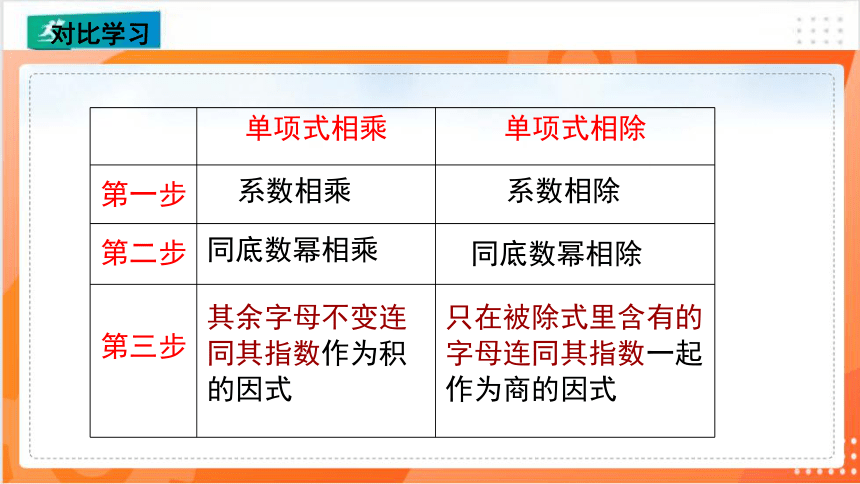
知识要点
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里作为因式.
被除式的系数
除式的系数
单项式除以单项式的法则
单项式相乘 单项式相除
第一步
第二步
第三步
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
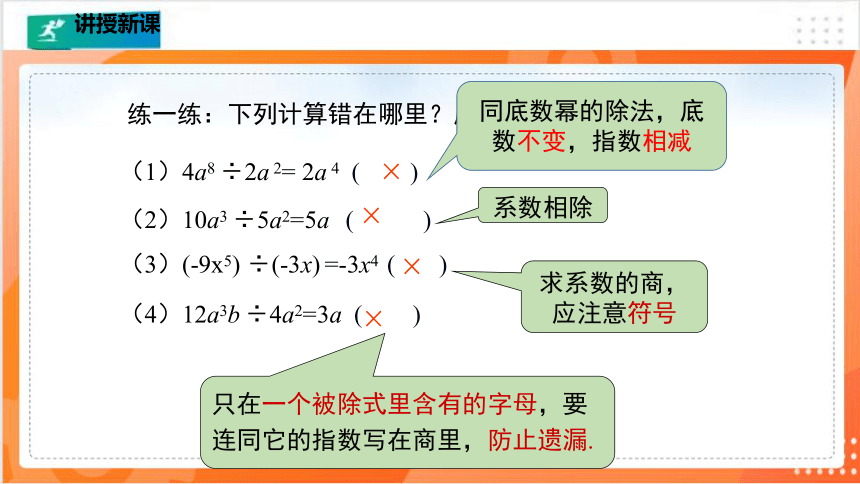
对比学习
讲授新课
练一练:下列计算错在哪里?应怎样改正?
×
×
×
×
(1)4a8 ÷2a 2= 2a 4 ( )
(2)10a3 ÷5a2=5a ( )
(3)(-9x5) ÷(-3x) =-3x4 ( )
(4)12a3b ÷4a2=3a ( )
系数相除
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求系数的商,应注意符号
同底数幂的除法,底数不变,指数相减
讲授新课
例1 计算:
(1) ; (2)10a4b3c2÷5a3bc ;
(3)(2x2y)3·(-7xy2) ÷14x4y3;(4)(2a+b)4÷ (2a+b)2.
解:(1)
(2)10a4b3c2÷5a3bc =(10÷5) a4-3b3-1c2-1=2ab2c;
(3)(2x2y)3·(-7xy2) ÷14x4y3 = 8x6y3·(-7xy2) ÷14x4y3
= -56x7y5 ÷14x4y3 = -4x3y2 ;
(4)(2a+b)4÷ (2a+b)2 = (2a+b)4-2
= (2a+b)2 = 4a2+4ab+b2 .
可以把(2a+b)看成一个整体,转化为单项式除以单项式
讲授新课
例2.计算下列各式
(1)
(2) (x+y)3 ÷ (x+y)2
注意运算顺序:同级运算,从左至右,依次计算
解:(1)原式
讲授新课
例2.计算下列各式
(1)
(2) (x+y)3 ÷ (x+y)2
可以把 (x+y)
看成一个整体
(2)原式
当堂检测
1. 计算(-2a3)2÷a2的结果是( )
A.-2a3 B.-2a4 C.4a3 D.4a4
2. 已知a≠0,下列运算中正确的是( )
A.3a+2a2=5a3 B.6a3÷2a2=3a
C.(3a3)2=6a6 D.3a3÷2a2=5a5
D
B
当堂检测
4.下列算式中,不正确的是( )
A.(-12a5b)÷(-3ab)=4a4
B.9xmyn-1÷3xm-2yn-3=3x2y2
C.4a2b3÷2ab=2ab2
D.x(x-y)2÷(y-x)=x(x-y)
3.下列运算中,正确的是( )
A.4a-a=3 B.a2+a3=a5 C.(-2a)3=-6a3 D.ab2÷a=b2
D
D
当堂检测
7. 计算:6x3÷2x=____.
3x2
6.计算12a5b4c4÷(-3a2b2c)÷2a3b2c3,其结果正确的是( )
A.-2 B.0 C.1 D.2
A
5.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
当堂检测
8.计算
(1)(2a2b2c)4z÷(-2ab2c2)2;
(2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
当堂检测
9.计算:
(1)28x4y2 ÷7x3y;
(2)-5a5b3c ÷15a4b.
=4xy;
(2)原式=(-5÷15)a5-4b3-1c
解:(1)原式=(28 ÷7)x4-3y2-1
= ab2c.
当堂检测
10.计算:(1)
(2)(b-2a)4÷(b-2a)2.
解: (1)原式
(2)原式=(b-2a)4-2
=(b-2a)2
=b2-4ab+4a2.
当堂检测
11.月球距离地球大约3.84×105千米, 一架飞机的速度约为 8×102 千米/时.如果乘坐此飞机飞行这么远的距离, 大约需要多少时间
解:3.84×105 ÷( 8×102 )
= 0.48×103 =480(小时) =20(天) .
答:如果乘坐此飞机飞行这么远的距离, 大约需要20天时间.
课堂小结
单项式除以单项式
法则
1.系数相除;
2.同底数的幂相除;
3.只在被除式里的因式照搬作为商的一个因式
注意
1.一个不变:对于只在被除式中含有的字母,连同它的指数一起作为商的一个因式.
2.二个相除:把各个单项式中的系数、同底数幂分别相除.
3.三个检验:单项式除以单项式的结果是否正确,可从以下三个方面来检验:(1)结果仍是单项式;(2)结果中的字母少于或等于被除式中的字母;(3)结果的次数等于被除式与除式的次数之差.
1.7.1整式的除法(1)
第一章
整式的乘除
2021-2022学年七年级数学下册同步(北师大版)
学习目标
1.理解和掌握单项式除以单项式的运算法则,运用运
算法则熟练、准确地进行计算.
2.通过总结法则,培养概括能力;训练综合解题能力
和计算能力.
导入新课
木星的质量约是1.9×1024吨,地球的质量约是5.98×1021吨,你知道木星的质量约为地球质量的多少倍吗
木星的质量约为地球质量的(1.90×1024)÷(5.98×1021)倍.
想一想:上面的式子该如何计算
地球
木星
学习了今天的知识,我们就能解决这个问题了!
讲授新课
单项式除以单项式
你能计算下列各题吗?如果能,说说你的理由.
(1)x5y÷x2=;
(2)8m2n2÷2m2n=;
(3)a4b2c÷3a2b=.
除法
乘法
互逆运算
( ). x2 =x5y
( ).2m2n=8m2n2
( ). 3a2b=a4b2c
讲授新课
方法2:利用类似分数约分的方法
约分时,先约系数,再约同底数幂,分子中单独存在的字母及其指数直接作为商的因式.
单项式相除, 把系数、同底数幂分别相除作为商的因式;对于只在被除式中出现的字母,则连同它的指数一起作为商的一个因式.
知识要点
商式=系数 同底的幂 被除式里单独有的幂
底数不变,
指数相减.
保留在商里作为因式.
被除式的系数
除式的系数
单项式除以单项式的法则
单项式相乘 单项式相除
第一步
第二步
第三步
系数相乘
系数相除
同底数幂相乘
同底数幂相除
其余字母不变连同其指数作为积的因式
只在被除式里含有的字母连同其指数一起作为商的因式
对比学习
讲授新课
练一练:下列计算错在哪里?应怎样改正?
×
×
×
×
(1)4a8 ÷2a 2= 2a 4 ( )
(2)10a3 ÷5a2=5a ( )
(3)(-9x5) ÷(-3x) =-3x4 ( )
(4)12a3b ÷4a2=3a ( )
系数相除
只在一个被除式里含有的字母,要连同它的指数写在商里,防止遗漏.
求系数的商,应注意符号
同底数幂的除法,底数不变,指数相减
讲授新课
例1 计算:
(1) ; (2)10a4b3c2÷5a3bc ;
(3)(2x2y)3·(-7xy2) ÷14x4y3;(4)(2a+b)4÷ (2a+b)2.
解:(1)
(2)10a4b3c2÷5a3bc =(10÷5) a4-3b3-1c2-1=2ab2c;
(3)(2x2y)3·(-7xy2) ÷14x4y3 = 8x6y3·(-7xy2) ÷14x4y3
= -56x7y5 ÷14x4y3 = -4x3y2 ;
(4)(2a+b)4÷ (2a+b)2 = (2a+b)4-2
= (2a+b)2 = 4a2+4ab+b2 .
可以把(2a+b)看成一个整体,转化为单项式除以单项式
讲授新课
例2.计算下列各式
(1)
(2) (x+y)3 ÷ (x+y)2
注意运算顺序:同级运算,从左至右,依次计算
解:(1)原式
讲授新课
例2.计算下列各式
(1)
(2) (x+y)3 ÷ (x+y)2
可以把 (x+y)
看成一个整体
(2)原式
当堂检测
1. 计算(-2a3)2÷a2的结果是( )
A.-2a3 B.-2a4 C.4a3 D.4a4
2. 已知a≠0,下列运算中正确的是( )
A.3a+2a2=5a3 B.6a3÷2a2=3a
C.(3a3)2=6a6 D.3a3÷2a2=5a5
D
B
当堂检测
4.下列算式中,不正确的是( )
A.(-12a5b)÷(-3ab)=4a4
B.9xmyn-1÷3xm-2yn-3=3x2y2
C.4a2b3÷2ab=2ab2
D.x(x-y)2÷(y-x)=x(x-y)
3.下列运算中,正确的是( )
A.4a-a=3 B.a2+a3=a5 C.(-2a)3=-6a3 D.ab2÷a=b2
D
D
当堂检测
7. 计算:6x3÷2x=____.
3x2
6.计算12a5b4c4÷(-3a2b2c)÷2a3b2c3,其结果正确的是( )
A.-2 B.0 C.1 D.2
A
5.已知28a3bm÷28anb2=b2,那么m,n的取值为( )
A.m=4,n=3 B.m=4,n=1
C.m=1,n=3 D.m=2,n=3
A
当堂检测
8.计算
(1)(2a2b2c)4z÷(-2ab2c2)2;
(2)(3x3y3z)4÷(3x3y2z)2÷x2y6z.
解:(1)原式=16a8b8c4z÷4a2b4c4=4a6b4z;
(2)原式=81x12y12z4÷9x6y4z2÷x2y6z=9x4y2z.
当堂检测
9.计算:
(1)28x4y2 ÷7x3y;
(2)-5a5b3c ÷15a4b.
=4xy;
(2)原式=(-5÷15)a5-4b3-1c
解:(1)原式=(28 ÷7)x4-3y2-1
= ab2c.
当堂检测
10.计算:(1)
(2)(b-2a)4÷(b-2a)2.
解: (1)原式
(2)原式=(b-2a)4-2
=(b-2a)2
=b2-4ab+4a2.
当堂检测
11.月球距离地球大约3.84×105千米, 一架飞机的速度约为 8×102 千米/时.如果乘坐此飞机飞行这么远的距离, 大约需要多少时间
解:3.84×105 ÷( 8×102 )
= 0.48×103 =480(小时) =20(天) .
答:如果乘坐此飞机飞行这么远的距离, 大约需要20天时间.
课堂小结
单项式除以单项式
法则
1.系数相除;
2.同底数的幂相除;
3.只在被除式里的因式照搬作为商的一个因式
注意
1.一个不变:对于只在被除式中含有的字母,连同它的指数一起作为商的一个因式.
2.二个相除:把各个单项式中的系数、同底数幂分别相除.
3.三个检验:单项式除以单项式的结果是否正确,可从以下三个方面来检验:(1)结果仍是单项式;(2)结果中的字母少于或等于被除式中的字母;(3)结果的次数等于被除式与除式的次数之差.
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
