1.7.2整式的除法(2) 课件(共23张PPT)
文档属性
| 名称 | 1.7.2整式的除法(2) 课件(共23张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 637.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
1.7.2整式的除法(2)
第一章
整式的乘除
2021-2022学年七年级数学下册同步(北师大版)
学习目标
1、经历探索多项式除以单项式法则的过程,会进行多项式除以单项式的运算。
2、掌握多项式除以单项式的运算算理.
3、在发展推理能力和有条理的表达能力的同时,体会学习数学的兴趣,培养学习数学的信心。
导入新课
(l)用式子表示乘法分配律.
(2)单项式除以单项式法则是什么?
单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
导入新课
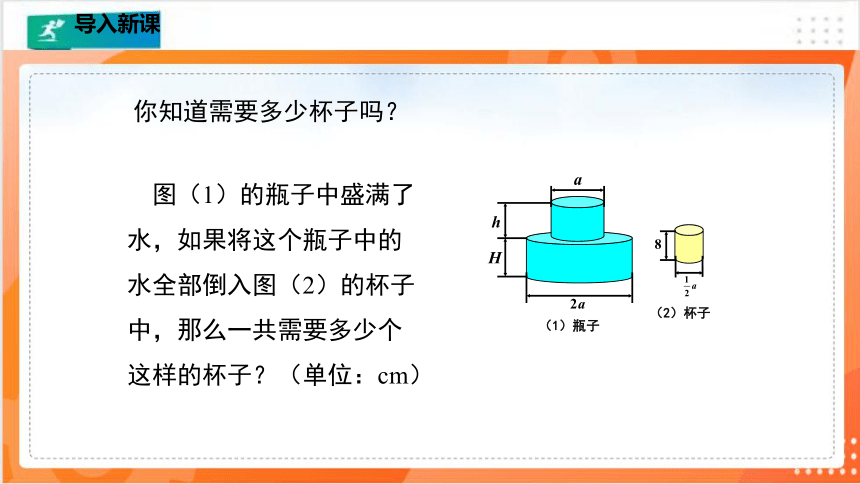
(1)瓶子
(2)杯子
图(1)的瓶子中盛满了水,如果将这个瓶子中的水全部倒入图(2)的杯子中,那么一共需要多少个这样的杯子?(单位:cm)
你知道需要多少杯子吗?
讲授新课
多项式除以单项式
完成下列各题:
(1)因为(____)c=ac+bc,所以(ac+bc)÷c=____.
(2)因为(______)b=ab2+3ab,所(ab2+3ab)÷b=______.
(3)由于(_____)xy=xy-xy2,所以(xy-xy2)÷xy= _____.
a+b
a+b
ab+3a
ab+3a
1-y
1-y
讲授新课
由以上解题我们不难得出:
(ac+bc)÷c=____=ac÷__+bc÷__.
(ab2+3ab)÷b=______=a2b÷__+3ab÷__.
(xy-xy2)÷xy= _____=xy÷___-xy2÷___.
a+b
ab+3a
b
1-y
xy
xy
c
c
b
讲授新课
由此,你能归纳出多项式除以单项式的法则吗?
【归纳】多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
【点拨】多项式除以单项式的运算是转化为单项式除以单项式来计算的,所以计算中要特别注意每项的符号.
讲授新课
【思考】
多项式中的某一项与除式完全相同时,相除后的结果是多少?
提示:相除的结果是1而不是0.
讲授新课
例1 计算:
(1) (6ab+8b)÷2b ;(2) (27a3-15a2+6a)÷3a ;
(3) (9x2y-6xy2)÷3xy;(4)
解:(1) (6ab+8b)÷2b
= 6ab÷2b+8b÷2b
= 3a+4 ;
(2) (27a3-15a2+6a)÷3a
= 27a3÷3a +(-15a2)÷3a +6a÷3a
=9a2-5a+2 ;
讲授新课
解:(3) (9x2y-6xy2)÷3xy
= 9x2y÷3xy +(-6xy2) ÷3xy
= 3x -2y;
(4)
例1 计算:
(1) (6ab+8b)÷2b ;(2) (27a3-15a2+6a)÷3a ;
(3) (9x2y-6xy2)÷3xy;(4)
讲授新课
总结:多项式除以单项式实质是转化为单项式除以单项式,计算时应注意逐项相除,不要漏项,并且要注意符号的变化,最后的结果通常要按某一字母升幂或降幂的顺序排列.
讲授新课
总结:多项式除以单项式中的“三数变化特点”
(1)项数:被除式有几项,则商就有几项,计算中不可漏项;
(2)系数:各项系数相除时,应包含前面的符号,当被除式的系数为负数时,商式的各项符号与被除多项式各项的符号相反;
(3)次数:商的次数小于或等于被除式的次数。
讲授新课
例2 已知一个多项式除以2x2,所得的商是2x2+1,余式是3x-2,请求出这个多项式.
解:根据题意得
2x2(2x2+1)+3x-2
=4x4+2x2+3x-2,
则这个多项式为4x4+2x2+3x-2.
方法总结:“被除式=商×除式+余式”
讲授新课
例3 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2017,y=2016.
解:[2x(x2y-xy2)+xy(xy-x2)]÷x2y
=[2x3y-2x2y2+x2y2-x3y]÷x2y
=x-y.
当x=2017,y=2016时,
原式=x-y=2017-2016=1.
方法总结:熟练掌握去括号,合并同类项,整式的除法的法则
当堂检测
1.计算(3x2-x)÷(-x)的正确结果是( )
A.3x B.3x-1
C.-3x+1 D.-3x-1
C
2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,则这个多项式为( )
A.4x2-3y2 B.4x2y-3xy2
C.4x2-3y2+14xy4 D.4x2-3y2+7xy3
C
当堂检测
5. 已知一多项式与单项式-7x5y4 的积为21x5y7-28x6y5,则这个多项式是 .
-3y3+4xy
4.一个长方形的面积为a2+2a,若一边长为a,则另一边长为_____________.
a+2
B
3.如果(4a2b-3ab2)÷M=-4a+3b,那么单项式M等于( )
A.ab B.-ab C.a D.-b
当堂检测
6.计算:(1)(6x3y4z-4x2y3z+2xy3)÷2xy3;
(2)(72x3y4-36x2y3+9xy2)÷(-9xy2).
(2)原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)
+9xy2÷(-9xy2)
=-8x2y2+4xy-1.
解:(1)原式=6x3y4z÷2xy3-4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz-2xz+1;
当堂检测
7.计算:(1)(12a3-6a2+3a) ÷3a;
解:(1) (12a3-6a2+3a) ÷3a
=12a3÷3a+(-6a2) ÷3a+3a÷3a
=4a2+(-2a)+1
=4a2-2a+1.
(2)(14m3-7m2+14m)÷7m.
(2)(14m3-7m2+14m)÷7m
=14m3÷7m-7m2÷7m+14m÷7m
= 2m2-m+2.
当堂检测
8.求值:(21x4y3-35x3y2+7x2y2)÷(-7x2y)
其中x=1,y=-2
解:原式
=21x4y3 ÷(-7x2y) -35x3y2
÷(-7x2y) +7x2y2 ÷(-7x2y)
=-3x2y2 + 5xy - y
把x=1,y=-2代入上式,得
原式=-3×12× (-2)2+5×1× (-2)-(-2)
=-12-10+2=-20.
当堂检测
9.先化简,再求值:(x+y)(x-y)-(4x3y-8xy3)÷2xy,其中x=1,y=-3.
解:原式=x2-y2-2x2+4y2
原式=-12+3×(-3)2=-1+27=26.
当x=1,y=-3时,
=-x2+3y2.
课堂小结
多项式除以单项式
法则
注意
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
(a+b+c) ÷m=a÷m+b÷m+c÷m (m≠0)
1.被除式有几项,则商就有几项,不可丢项.
2.各项系数相除时,应包含前面的符号.当除式的系数为负数时,商式的各项符号与被除多项式各项的符号相反.
3.商的次数小于或等于被除式的次数.
方法
转化为单项式除以单项式的问题
https://www.21cnjy.com/help/help_extract.php
1.7.2整式的除法(2)
第一章
整式的乘除
2021-2022学年七年级数学下册同步(北师大版)
学习目标
1、经历探索多项式除以单项式法则的过程,会进行多项式除以单项式的运算。
2、掌握多项式除以单项式的运算算理.
3、在发展推理能力和有条理的表达能力的同时,体会学习数学的兴趣,培养学习数学的信心。
导入新课
(l)用式子表示乘法分配律.
(2)单项式除以单项式法则是什么?
单项式相除,把系数、同底数幂分别相除后,作为商的因式;对于只在被除式里含有的字母,则连同它的指数一起作为商的一个因式.
导入新课
(1)瓶子
(2)杯子
图(1)的瓶子中盛满了水,如果将这个瓶子中的水全部倒入图(2)的杯子中,那么一共需要多少个这样的杯子?(单位:cm)
你知道需要多少杯子吗?
讲授新课
多项式除以单项式
完成下列各题:
(1)因为(____)c=ac+bc,所以(ac+bc)÷c=____.
(2)因为(______)b=ab2+3ab,所(ab2+3ab)÷b=______.
(3)由于(_____)xy=xy-xy2,所以(xy-xy2)÷xy= _____.
a+b
a+b
ab+3a
ab+3a
1-y
1-y
讲授新课
由以上解题我们不难得出:
(ac+bc)÷c=____=ac÷__+bc÷__.
(ab2+3ab)÷b=______=a2b÷__+3ab÷__.
(xy-xy2)÷xy= _____=xy÷___-xy2÷___.
a+b
ab+3a
b
1-y
xy
xy
c
c
b
讲授新课
由此,你能归纳出多项式除以单项式的法则吗?
【归纳】多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.
【点拨】多项式除以单项式的运算是转化为单项式除以单项式来计算的,所以计算中要特别注意每项的符号.
讲授新课
【思考】
多项式中的某一项与除式完全相同时,相除后的结果是多少?
提示:相除的结果是1而不是0.
讲授新课
例1 计算:
(1) (6ab+8b)÷2b ;(2) (27a3-15a2+6a)÷3a ;
(3) (9x2y-6xy2)÷3xy;(4)
解:(1) (6ab+8b)÷2b
= 6ab÷2b+8b÷2b
= 3a+4 ;
(2) (27a3-15a2+6a)÷3a
= 27a3÷3a +(-15a2)÷3a +6a÷3a
=9a2-5a+2 ;
讲授新课
解:(3) (9x2y-6xy2)÷3xy
= 9x2y÷3xy +(-6xy2) ÷3xy
= 3x -2y;
(4)
例1 计算:
(1) (6ab+8b)÷2b ;(2) (27a3-15a2+6a)÷3a ;
(3) (9x2y-6xy2)÷3xy;(4)
讲授新课
总结:多项式除以单项式实质是转化为单项式除以单项式,计算时应注意逐项相除,不要漏项,并且要注意符号的变化,最后的结果通常要按某一字母升幂或降幂的顺序排列.
讲授新课
总结:多项式除以单项式中的“三数变化特点”
(1)项数:被除式有几项,则商就有几项,计算中不可漏项;
(2)系数:各项系数相除时,应包含前面的符号,当被除式的系数为负数时,商式的各项符号与被除多项式各项的符号相反;
(3)次数:商的次数小于或等于被除式的次数。
讲授新课
例2 已知一个多项式除以2x2,所得的商是2x2+1,余式是3x-2,请求出这个多项式.
解:根据题意得
2x2(2x2+1)+3x-2
=4x4+2x2+3x-2,
则这个多项式为4x4+2x2+3x-2.
方法总结:“被除式=商×除式+余式”
讲授新课
例3 先化简,后求值:[2x(x2y-xy2)+xy(xy-x2)]÷x2y,其中x=2017,y=2016.
解:[2x(x2y-xy2)+xy(xy-x2)]÷x2y
=[2x3y-2x2y2+x2y2-x3y]÷x2y
=x-y.
当x=2017,y=2016时,
原式=x-y=2017-2016=1.
方法总结:熟练掌握去括号,合并同类项,整式的除法的法则
当堂检测
1.计算(3x2-x)÷(-x)的正确结果是( )
A.3x B.3x-1
C.-3x+1 D.-3x-1
C
2.5x3y2与一个多项式的积为20x5y2-15x3y4+70(x2y3)2,则这个多项式为( )
A.4x2-3y2 B.4x2y-3xy2
C.4x2-3y2+14xy4 D.4x2-3y2+7xy3
C
当堂检测
5. 已知一多项式与单项式-7x5y4 的积为21x5y7-28x6y5,则这个多项式是 .
-3y3+4xy
4.一个长方形的面积为a2+2a,若一边长为a,则另一边长为_____________.
a+2
B
3.如果(4a2b-3ab2)÷M=-4a+3b,那么单项式M等于( )
A.ab B.-ab C.a D.-b
当堂检测
6.计算:(1)(6x3y4z-4x2y3z+2xy3)÷2xy3;
(2)(72x3y4-36x2y3+9xy2)÷(-9xy2).
(2)原式=72x3y4÷(-9xy2)+(-36x2y3)÷(-9xy2)
+9xy2÷(-9xy2)
=-8x2y2+4xy-1.
解:(1)原式=6x3y4z÷2xy3-4x2y3z÷2xy3+2xy3÷2xy3
=3x2yz-2xz+1;
当堂检测
7.计算:(1)(12a3-6a2+3a) ÷3a;
解:(1) (12a3-6a2+3a) ÷3a
=12a3÷3a+(-6a2) ÷3a+3a÷3a
=4a2+(-2a)+1
=4a2-2a+1.
(2)(14m3-7m2+14m)÷7m.
(2)(14m3-7m2+14m)÷7m
=14m3÷7m-7m2÷7m+14m÷7m
= 2m2-m+2.
当堂检测
8.求值:(21x4y3-35x3y2+7x2y2)÷(-7x2y)
其中x=1,y=-2
解:原式
=21x4y3 ÷(-7x2y) -35x3y2
÷(-7x2y) +7x2y2 ÷(-7x2y)
=-3x2y2 + 5xy - y
把x=1,y=-2代入上式,得
原式=-3×12× (-2)2+5×1× (-2)-(-2)
=-12-10+2=-20.
当堂检测
9.先化简,再求值:(x+y)(x-y)-(4x3y-8xy3)÷2xy,其中x=1,y=-3.
解:原式=x2-y2-2x2+4y2
原式=-12+3×(-3)2=-1+27=26.
当x=1,y=-3时,
=-x2+3y2.
课堂小结
多项式除以单项式
法则
注意
多项式除以单项式,先把这个多项式的每一项除以这个单项式,再把所得的商相加.
(a+b+c) ÷m=a÷m+b÷m+c÷m (m≠0)
1.被除式有几项,则商就有几项,不可丢项.
2.各项系数相除时,应包含前面的符号.当除式的系数为负数时,商式的各项符号与被除多项式各项的符号相反.
3.商的次数小于或等于被除式的次数.
方法
转化为单项式除以单项式的问题
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
