11.2全等三角形的判定(1)学案
文档属性
| 名称 | 11.2全等三角形的判定(1)学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 24.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-26 00:00:00 | ||
图片预览

文档简介
§11.2全等三角形的判定(1)课堂练习学案
一、判定定理
1、探究:按下列要求画三角形(与同桌所画的三角形比较):
(1)画△ABC,使∠A=30゜,∠B=50゜;(2)画△ABC,使∠A=30゜,AB=3cm;
(3)画△ABC,使AB=3cm,BC=4cm.
结论:满足一个或两个条件, (能否)判定两个三角形全等.
2、探究:按下列要求画三角形(与同桌所画的三角形比较):
(1)画△ABC,使∠A=30゜,∠B=60゜,∠C=90゜;
结论: .
(2)已知线段AB,作线段A1B1=AB.
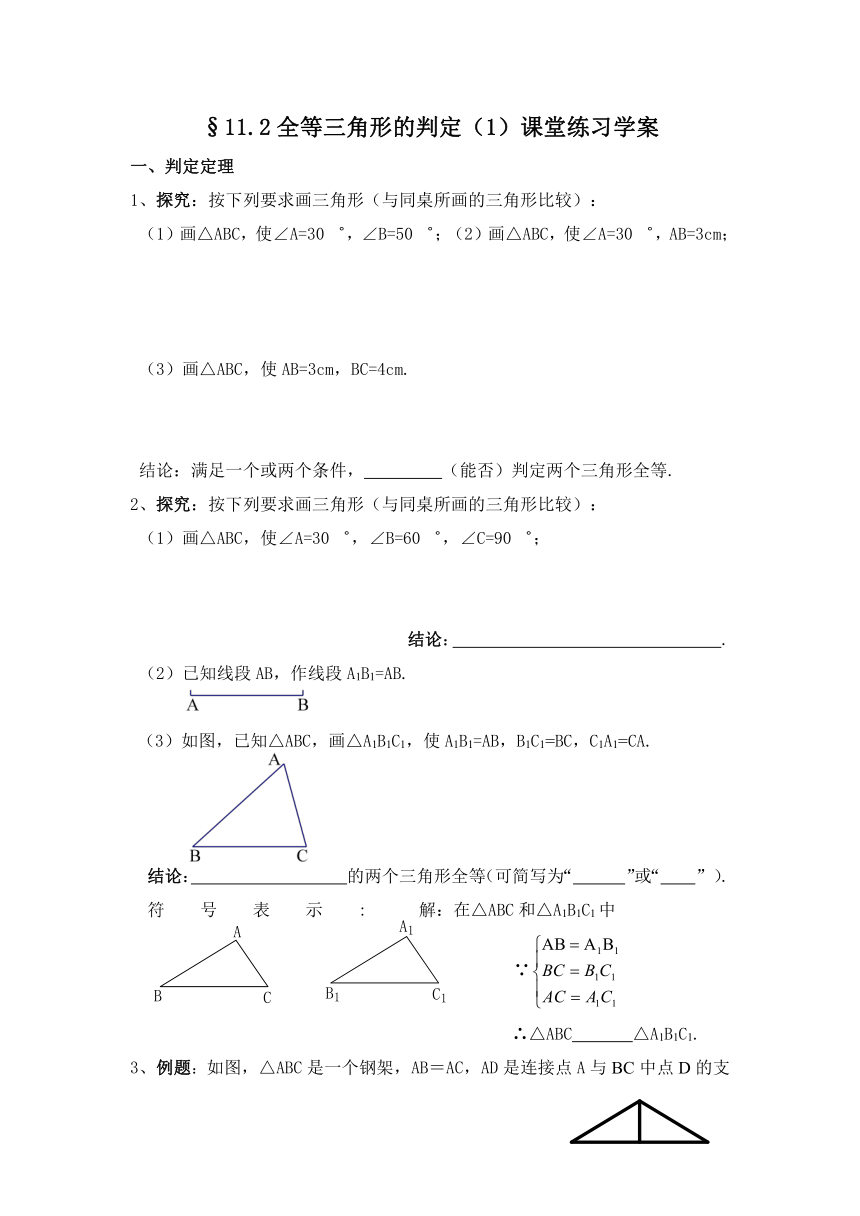
(3)如图,已知△ABC,画△A1B1C1,使A1B1=AB,B1C1=BC,C1A1=CA.
结论: 的两个三角形全等(可简写为“ ”或“ ” ).
符号表示: 解:在△ABC和△A1B1C1中
∵
∴△ABC △A1B1C1.
3、例题:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
课堂练习:
1、如图,点A、C、F、D在同一直线上,AB=DE,BC=EF,AF=DC.求证:∠B=∠E.
2、如右图,AB=DC,AC=DB,∠2=40o,
∠3=80o,则∠A的度数是 .
3、如图,AB=CD,AD=CB.求证:(1)∠A=∠C;(2)AB∥DC,AD∥BC.
4、作图:已知∠AOB,求作∠A1O1B1,使∠A1O1B1=∠AOB.
一、判定定理
1、探究:按下列要求画三角形(与同桌所画的三角形比较):
(1)画△ABC,使∠A=30゜,∠B=50゜;(2)画△ABC,使∠A=30゜,AB=3cm;
(3)画△ABC,使AB=3cm,BC=4cm.
结论:满足一个或两个条件, (能否)判定两个三角形全等.
2、探究:按下列要求画三角形(与同桌所画的三角形比较):
(1)画△ABC,使∠A=30゜,∠B=60゜,∠C=90゜;
结论: .
(2)已知线段AB,作线段A1B1=AB.
(3)如图,已知△ABC,画△A1B1C1,使A1B1=AB,B1C1=BC,C1A1=CA.
结论: 的两个三角形全等(可简写为“ ”或“ ” ).
符号表示: 解:在△ABC和△A1B1C1中
∵
∴△ABC △A1B1C1.
3、例题:如图,△ABC是一个钢架,AB=AC,AD是连接点A与BC中点D的支架.求证△ABD≌△ACD.
课堂练习:
1、如图,点A、C、F、D在同一直线上,AB=DE,BC=EF,AF=DC.求证:∠B=∠E.
2、如右图,AB=DC,AC=DB,∠2=40o,
∠3=80o,则∠A的度数是 .
3、如图,AB=CD,AD=CB.求证:(1)∠A=∠C;(2)AB∥DC,AD∥BC.
4、作图:已知∠AOB,求作∠A1O1B1,使∠A1O1B1=∠AOB.
