6.4三角形的中位线定理同步练习2021-2022学年青岛版八年级数学下册(word版含答案)
文档属性
| 名称 | 6.4三角形的中位线定理同步练习2021-2022学年青岛版八年级数学下册(word版含答案) |

|
|
| 格式 | docx | ||
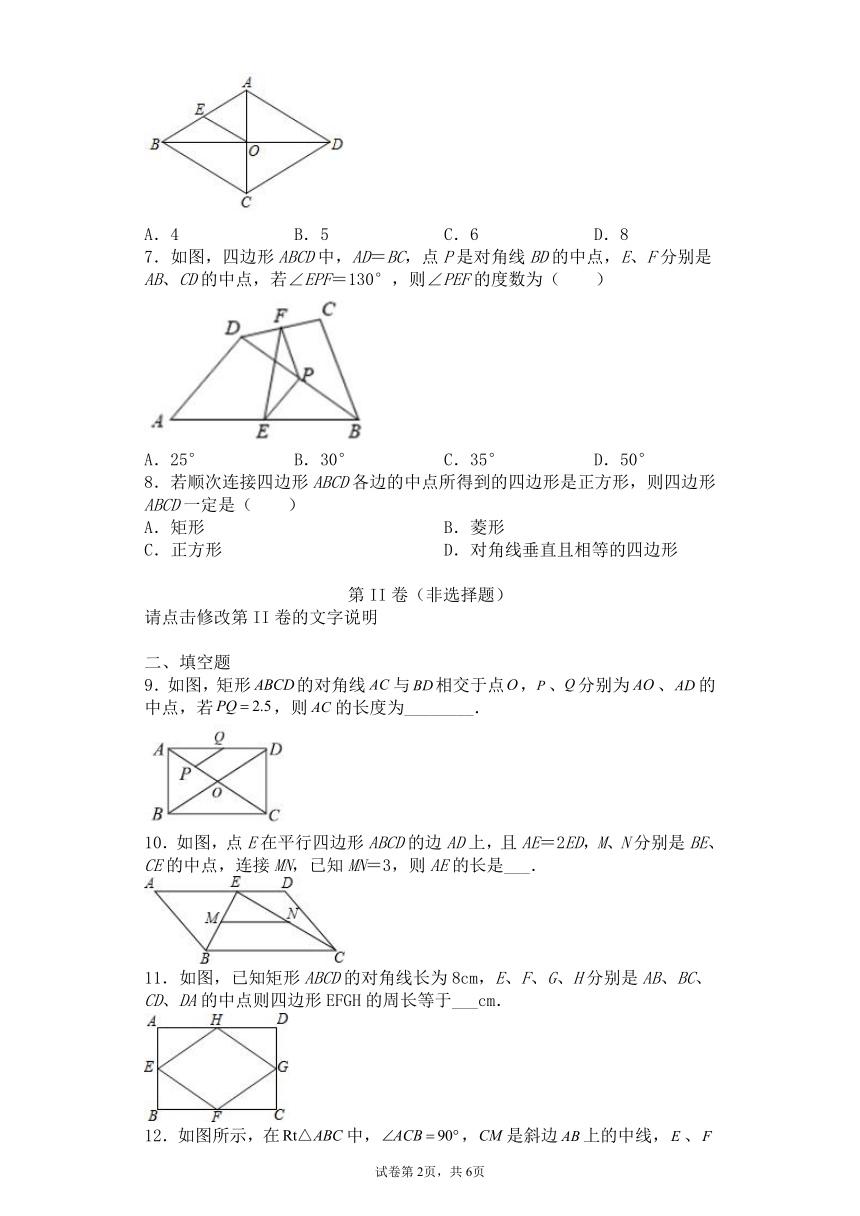
| 文件大小 | 481.6KB | ||
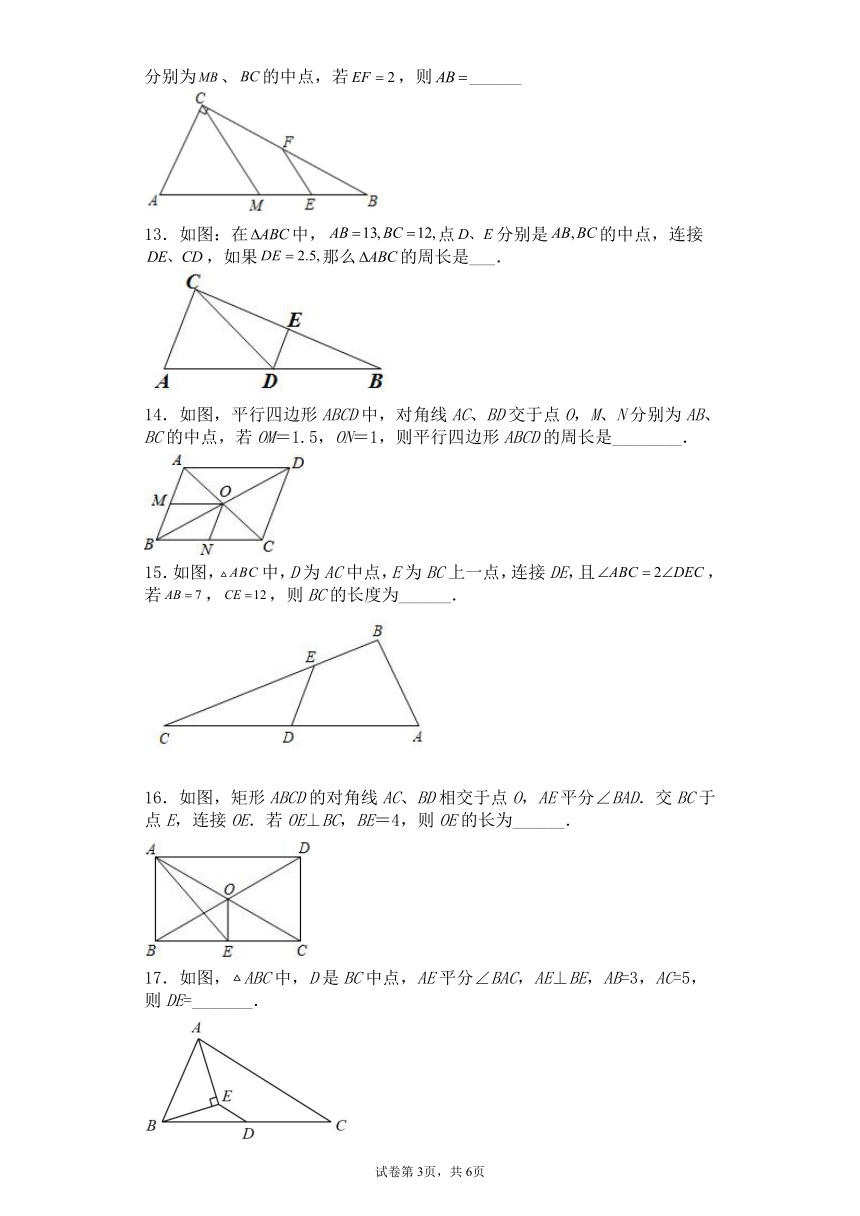
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览

文档简介
6.4 三角形的中位线定理
一、选择题
1.如图,DE是的中位线,若,则BC的长为( )
A.8 B.7 C.6 D.7.5
2.如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐变小
C.线段EF的长不变 D.无法确定
3.连结三角形两边中点的线段叫做三角形的( )
A.中线 B.中垂线 C.中位线 D.中间线
4.如图,在菱形ABCD中,E,F分别是AD、AC的中点,若,则菱形ABCD的周长是( )
A.6 B.18 C.24 D.30
5.如图,在中,、分别为、的中点,平分,交于点,若,则的长为( )
A.1 B.2 C.3 D.4
6.菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点.若菱形ABCD的周长为32,则OE的长为( )
A.4 B.5 C.6 D.8
7.如图,四边形ABCD中,AD=BC,点P是对角线BD的中点,E、F分别是AB、CD的中点,若∠EPF=130°,则∠PEF的度数为( )
A.25° B.30° C.35° D.50°
8.若顺次连接四边形ABCD各边的中点所得到的四边形是正方形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.正方形 D.对角线垂直且相等的四边形
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
9.如图,矩形的对角线与相交于点,、分别为、的中点,若,则的长度为________.
10.如图,点E在平行四边形ABCD的边AD上,且AE=2ED,M、N分别是BE、CE的中点,连接MN,已知MN=3,则AE的长是___.
11.如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点则四边形EFGH的周长等于___cm.
12.如图所示,在中,,是斜边上的中线,、分别为、的中点,若,则______
13.如图:在中,点分别是的中点,连接,如果那么的周长是___.
14.如图,平行四边形ABCD中,对角线AC、BD交于点O,M、N分别为AB、BC的中点,若OM=1.5,ON=1,则平行四边形ABCD的周长是________.
15.如图,中,D为AC中点,E为BC上一点,连接DE,且,若,,则BC的长度为______.
16.如图,矩形ABCD的对角线AC、BD相交于点O,AE平分∠BAD.交BC于点E,连接OE.若OE⊥BC,BE=4,则OE的长为______.
17.如图,ABC中,D是BC中点,AE平分∠BAC,AE⊥BE,AB=3,AC=5,则DE=_______.
三、解答题
18.如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF.求证:四边形ADEF是平行四边形.
19.如图,点D、F分别为AC、BC的中点,,,求证:
20.如图,在□ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
21.已知:平行四边形ABCD,对角线AC,BD相交于点O.E是AD的中点,连接OE并延长至F使得,连接FD,FC,FC交BD于点G.
(1)求证:四边形FOCD是平行四边形;
(2)当AB与AC的数量关系满足______时,四边形FOCD是菱形.
22.如图,ABC的中线BE,CD相交于点O,F、G分别是BO、CO的中点,连结DF,EG,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.
23.如图,在中,,,是的中位线,连接,.求证:.
24.在ABC中,D、E、F分别是AB、AC、BC的中点,连接DE、DF.
(1)如图1,若AC=BC,求证:四边形DECF为菱形;
(2)如图2,过C作CGAB交DE延长线于点G,连接EF,AG,在不添加任何辅助线的情况下,写出图中所有与ADG面积相等的平行四边形.
25.如图,BE,CF是△ABC的角平分线,AN⊥BE于N,AM⊥CF于M,求证:MN∥BC.
26.如图,四边形ABCD中,已知:A(a,0),B(0,b),C(c,0)和D(0,d).
(1)当四边形ABCD正方形时,写出a,b,c,d满足的等式关系 :
(2)若AB、BC、CD、DA的中点分别为E、F、G、H.
①直接写出E、F、G、H四点的坐标;
②证明:四边形EFGH是矩形;
③若矩形EFGH是正方形,则a,b,c,d满足的等式关系是 .
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】
是的中位线,,
,
故选:A.
2.C
【解析】
解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,为定值.
∴线段EF的长不改变.
故选:C.
3.C
【解析】
解:连结三角形两边中点的线段叫做三角形的中位线.
故选择C.
4.C
【解析】
解:∵E、F分别是AD、AC的中点,
∴EF是△ADC的中位线,
∴DC=2EF=2×3=6,
∴菱形ABCD的周长=4×6=24.
故选:C.
5.B
【解析】
解:∵、分别为、的中点,
∴,,
∴,
∵平分,
∴,
∴,
∴,
故选:B.
6.A
【解析】
解:∵四边形ABCD是菱形,对角线AC,BD相交于点O,
∴AB=BC=CD=AD,O是AC的中点,
∵菱形ABCD的周长为32,
∴AD=8,
∵E为AB边中点,
∴OE是△ABD的中位线,
∴,
故选A.
7.A
【解析】
解:∵点P是对角线BD的中点,E、F分别是AB、CD的中点,
∴ ,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∵∠EPF=130°,
∴ .
故选:A
8.D
【解析】
已知:如下图,四边形EFGH是正方形,且E、F、G、H分别是AB、BC、CD、AD的中点,
求证:四边形ABCD是对角线垂直且相等的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是正方形,即EF⊥FG,FE=FG,
∴AC⊥BD,AC=BD,
故选:D.
9.
【解析】
解:∵、分别为、的中点,
∴PQ是△AOD的中位线,
∴OD=2PQ=5.
又∵四边形ABCD是矩形,
∴AC=BD=2OD=25=10.
故答案为:10.
10.4
【解析】
解:∵M、N分别是BE、CE的中点,
∴BC=2MN=6,
∵四边形ABCD是平行四边形,
∴AD=BC=6,
∵AE=2ED,
∴ ,
故答案为:4.
11.16.
【解析】
如图,连接AC、BD,
∵四边形ABCD是矩形,
∴AC=BD=8cm,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HG=EF=AC=4cm,
EH=FG=BD=4cm,
∴四边形EFGH的周长=HG+EF+EH+FG=4cm+4cm+4cm+4cm=16cm,
故答案为:16.
12.8
【解析】
解:∵,是斜边上的中线,
∴CM=AM=BM=,
∵、分别为、的中点,
∴EF为△BCM的中位线,
∴CM=2EF,
∵,
∴CM=2EF=4,
∴CM==4,
∴AB=8,
故答案为:8.
13.30
【解析】
∵点 D 、 E 分别是 AB 、 BC 的中点,
∴DE是ΔABC的中位线,
∴ DE=AC ,
∵ DE=2.5 ,
∴ AC=5 ,
∵ AB=13 , BC=12 ,
∴ C△ABC=AB+BC+AC=13+12+5=30.
故答案为:30.
14.10
【解析】
解:∵四边形ABCD是平行四边形,
∴BO=DO,AD=BC,AB=CD,
∵M、N分别为AB、BC的中点,
∴MO=AD,NO=CD,
∵OM=1.5,ON=1,
∴AD=3,CD=2,
∴平行四边形ABCD的周长是:3+3+2+2=10,
故答案为:10.
15.17
【解析】
如图,取BC的中点F,连接DF
则BC=2CF
∵D点是AC的中点
∴DF是△ABC的中位线
∴,DF∥AB
∴∠CFD=∠ABC
∵
∴∠CFD=2∠DEC
∵∠CFD=∠DEC+∠FDE
∴∠DEC=∠FDE
∴
∴
∴
故答案为:17
16.2
【解析】
解:在矩形ABCD中,∠BAD=∠ABC=90°,OA=OC,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴AB= BE=4,
∵OE⊥BC,
∴AB,
∴OE=,
故答案为:2.
17.1
【解析】
解:延长BE交AC于F,
∵AE平分∠BAC,BE⊥AE,
∴∠BAE=∠CAE,∠AEB=∠AEF=90°,
在△ABE与△AFE中,
,
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,
∵AB=3,
∴AF=3,
∵AC=5,
∴CF=AC-AF=5-3=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=CF=1,
故答案为:1.
18.
【解析】
证明:∵点D,E分别是边BC,AC的中点,
∴DE∥BF,DE=AB,
∵AF=AB,
∴DE=AF,
∴四边形ADEF是平行四边形.
19.
【解析】
证明:∵点分别为的中点,
是的中位线,
∴,
∴,
在和中,,
∴,
∴.
20.
【解析】
证明:连接AC,如图所示.
∵点E是AB的中点,点F是BC的中点,
∴EF∥AC,EF=AC.
同理,可得出:HG∥AC,HG=AC,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形.
21.(1)见解析;(2)AB=AC.
(1)解:证明:在△ACD中,点O,E分别为边AC,AD中点,
∴OE为△ACD的中位线,
∴OE∥CD,OE=CD,
又∵OE=OF,
∴OF∥CD,OF=CD,
∴四边形OCDF为平行四边形;
(2)解:当AB=AC时,四边形FOCD是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,OC=AC,
∵AB=AC,
∴AB=CD=OC,
由(1)得:四边形OCDF为平行四边形,
∴平行四边形FOCD是菱形,
故答案案为:AB=AC.
22.DF∥EG,DF=EG,证明见解析
【解析】
解:DF∥EG,DF=EG,证明如下:
连接AO,
∵BE是AC的中线,
∴E是AC的中点,
又∵G是OC的中点,
∴GE是△ACO的中位线,
∴,GE∥AO,
同理可证明DF是△ABO的中位线,
∴,DF∥AO,
∴DF∥EG,DF=EG.
23.
【解析】
证明:∵DE、DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形DEAF是平行四边形,
∵∠CAB=90°,
∴四边形DEAF是矩形,
∴EF=AD.
24.
【解析】
解:(1)∵D、E、F分别是AB、AC、BC的中点,
∴DE、DF分别是△ABC中BC边、AC边上的中位线,
∴DE∥BC,DE=BC,DF∥AC,DF=AC,
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形,
又∵AC=BC,
∴DF=DE,
∴为菱形;
(2)∵,,
∴四边形是平行四边形,
∴与ADG面积相等的平行四边形有:
DECF,DEFB,EGCF,AEFD.
25.
【解析】
证明:如图,延长AN、AM分别交BC于点D、G.
∵BE为∠ABC的角平分线,BE⊥AG,
∴∠ABN=∠GBN,∠ANB=∠GNB=90°,
∴∠BAG=∠BGA,
∴△ABG为等腰三角形,
∴BN也为等腰三角形的中线,即AN=GN.
同理AM=DM,
∴MN为△ADG的中位线,
∴MN∥DG,
∴MN∥BC.
26.
【解析】
(1)解:四边形是正方形,
,
;
(2)①解:,,,,、、、的中点分别为、、、,
,,,,,,,;
②证明:、为、的中点,
是的中位线,
,,
同理:,,
,,
四边形是平行四边形,
,,,
,
,
平行四边形是矩形;
③解:由①得:,,,,,,,,
矩形是正方形,
,
,
,
故答案为:.
答案第8页,共9页
一、选择题
1.如图,DE是的中位线,若,则BC的长为( )
A.8 B.7 C.6 D.7.5
2.如图,已知P、R分别是长方形ABCD的边BC、CD上的点,E、F分别是PA、PR的中点,点P在BC上从B向C移动,点R不动,那么下列结论成立的是( )
A.线段EF的长逐渐增大 B.线段EF的长逐渐变小
C.线段EF的长不变 D.无法确定
3.连结三角形两边中点的线段叫做三角形的( )
A.中线 B.中垂线 C.中位线 D.中间线
4.如图,在菱形ABCD中,E,F分别是AD、AC的中点,若,则菱形ABCD的周长是( )
A.6 B.18 C.24 D.30
5.如图,在中,、分别为、的中点,平分,交于点,若,则的长为( )
A.1 B.2 C.3 D.4
6.菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点.若菱形ABCD的周长为32,则OE的长为( )
A.4 B.5 C.6 D.8
7.如图,四边形ABCD中,AD=BC,点P是对角线BD的中点,E、F分别是AB、CD的中点,若∠EPF=130°,则∠PEF的度数为( )
A.25° B.30° C.35° D.50°
8.若顺次连接四边形ABCD各边的中点所得到的四边形是正方形,则四边形ABCD一定是( )
A.矩形 B.菱形
C.正方形 D.对角线垂直且相等的四边形
第II卷(非选择题)
请点击修改第II卷的文字说明
二、填空题
9.如图,矩形的对角线与相交于点,、分别为、的中点,若,则的长度为________.
10.如图,点E在平行四边形ABCD的边AD上,且AE=2ED,M、N分别是BE、CE的中点,连接MN,已知MN=3,则AE的长是___.
11.如图,已知矩形ABCD的对角线长为8cm,E、F、G、H分别是AB、BC、CD、DA的中点则四边形EFGH的周长等于___cm.
12.如图所示,在中,,是斜边上的中线,、分别为、的中点,若,则______
13.如图:在中,点分别是的中点,连接,如果那么的周长是___.
14.如图,平行四边形ABCD中,对角线AC、BD交于点O,M、N分别为AB、BC的中点,若OM=1.5,ON=1,则平行四边形ABCD的周长是________.
15.如图,中,D为AC中点,E为BC上一点,连接DE,且,若,,则BC的长度为______.
16.如图,矩形ABCD的对角线AC、BD相交于点O,AE平分∠BAD.交BC于点E,连接OE.若OE⊥BC,BE=4,则OE的长为______.
17.如图,ABC中,D是BC中点,AE平分∠BAC,AE⊥BE,AB=3,AC=5,则DE=_______.
三、解答题
18.如图,△ABC中,点D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF.求证:四边形ADEF是平行四边形.
19.如图,点D、F分别为AC、BC的中点,,,求证:
20.如图,在□ABCD中,点E,F,G,H分别是AB,BC,CD,DA的中点.求证:四边形EFGH是平行四边形.
21.已知:平行四边形ABCD,对角线AC,BD相交于点O.E是AD的中点,连接OE并延长至F使得,连接FD,FC,FC交BD于点G.
(1)求证:四边形FOCD是平行四边形;
(2)当AB与AC的数量关系满足______时,四边形FOCD是菱形.
22.如图,ABC的中线BE,CD相交于点O,F、G分别是BO、CO的中点,连结DF,EG,试猜想DF与EG有怎样的数量关系和位置关系?并证明你的猜想.
23.如图,在中,,,是的中位线,连接,.求证:.
24.在ABC中,D、E、F分别是AB、AC、BC的中点,连接DE、DF.
(1)如图1,若AC=BC,求证:四边形DECF为菱形;
(2)如图2,过C作CGAB交DE延长线于点G,连接EF,AG,在不添加任何辅助线的情况下,写出图中所有与ADG面积相等的平行四边形.
25.如图,BE,CF是△ABC的角平分线,AN⊥BE于N,AM⊥CF于M,求证:MN∥BC.
26.如图,四边形ABCD中,已知:A(a,0),B(0,b),C(c,0)和D(0,d).
(1)当四边形ABCD正方形时,写出a,b,c,d满足的等式关系 :
(2)若AB、BC、CD、DA的中点分别为E、F、G、H.
①直接写出E、F、G、H四点的坐标;
②证明:四边形EFGH是矩形;
③若矩形EFGH是正方形,则a,b,c,d满足的等式关系是 .
试卷第2页,共2页
试卷第1页,共1页
参考答案
1.A
【解析】
是的中位线,,
,
故选:A.
2.C
【解析】
解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,为定值.
∴线段EF的长不改变.
故选:C.
3.C
【解析】
解:连结三角形两边中点的线段叫做三角形的中位线.
故选择C.
4.C
【解析】
解:∵E、F分别是AD、AC的中点,
∴EF是△ADC的中位线,
∴DC=2EF=2×3=6,
∴菱形ABCD的周长=4×6=24.
故选:C.
5.B
【解析】
解:∵、分别为、的中点,
∴,,
∴,
∵平分,
∴,
∴,
∴,
故选:B.
6.A
【解析】
解:∵四边形ABCD是菱形,对角线AC,BD相交于点O,
∴AB=BC=CD=AD,O是AC的中点,
∵菱形ABCD的周长为32,
∴AD=8,
∵E为AB边中点,
∴OE是△ABD的中位线,
∴,
故选A.
7.A
【解析】
解:∵点P是对角线BD的中点,E、F分别是AB、CD的中点,
∴ ,
∵AD=BC,
∴PE=PF,
∴∠PEF=∠PFE,
∵∠EPF=130°,
∴ .
故选:A
8.D
【解析】
已知:如下图,四边形EFGH是正方形,且E、F、G、H分别是AB、BC、CD、AD的中点,
求证:四边形ABCD是对角线垂直且相等的四边形.
证明:由于E、F、G、H分别是AB、BC、CD、AD的中点,
根据三角形中位线定理得:EH∥FG∥BD,EF∥AC∥HG;
∵四边形EFGH是正方形,即EF⊥FG,FE=FG,
∴AC⊥BD,AC=BD,
故选:D.
9.
【解析】
解:∵、分别为、的中点,
∴PQ是△AOD的中位线,
∴OD=2PQ=5.
又∵四边形ABCD是矩形,
∴AC=BD=2OD=25=10.
故答案为:10.
10.4
【解析】
解:∵M、N分别是BE、CE的中点,
∴BC=2MN=6,
∵四边形ABCD是平行四边形,
∴AD=BC=6,
∵AE=2ED,
∴ ,
故答案为:4.
11.16.
【解析】
如图,连接AC、BD,
∵四边形ABCD是矩形,
∴AC=BD=8cm,
∵E、F、G、H分别是AB、BC、CD、DA的中点,
∴HG=EF=AC=4cm,
EH=FG=BD=4cm,
∴四边形EFGH的周长=HG+EF+EH+FG=4cm+4cm+4cm+4cm=16cm,
故答案为:16.
12.8
【解析】
解:∵,是斜边上的中线,
∴CM=AM=BM=,
∵、分别为、的中点,
∴EF为△BCM的中位线,
∴CM=2EF,
∵,
∴CM=2EF=4,
∴CM==4,
∴AB=8,
故答案为:8.
13.30
【解析】
∵点 D 、 E 分别是 AB 、 BC 的中点,
∴DE是ΔABC的中位线,
∴ DE=AC ,
∵ DE=2.5 ,
∴ AC=5 ,
∵ AB=13 , BC=12 ,
∴ C△ABC=AB+BC+AC=13+12+5=30.
故答案为:30.
14.10
【解析】
解:∵四边形ABCD是平行四边形,
∴BO=DO,AD=BC,AB=CD,
∵M、N分别为AB、BC的中点,
∴MO=AD,NO=CD,
∵OM=1.5,ON=1,
∴AD=3,CD=2,
∴平行四边形ABCD的周长是:3+3+2+2=10,
故答案为:10.
15.17
【解析】
如图,取BC的中点F,连接DF
则BC=2CF
∵D点是AC的中点
∴DF是△ABC的中位线
∴,DF∥AB
∴∠CFD=∠ABC
∵
∴∠CFD=2∠DEC
∵∠CFD=∠DEC+∠FDE
∴∠DEC=∠FDE
∴
∴
∴
故答案为:17
16.2
【解析】
解:在矩形ABCD中,∠BAD=∠ABC=90°,OA=OC,
∵AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴∠AEB=45°,
∴AB= BE=4,
∵OE⊥BC,
∴AB,
∴OE=,
故答案为:2.
17.1
【解析】
解:延长BE交AC于F,
∵AE平分∠BAC,BE⊥AE,
∴∠BAE=∠CAE,∠AEB=∠AEF=90°,
在△ABE与△AFE中,
,
∴△ABE≌△AFE(ASA),
∴BE=EF,AB=AF,
∵AB=3,
∴AF=3,
∵AC=5,
∴CF=AC-AF=5-3=2,
∵D为BC中点,
∴BD=CD,
∴DE是△BCF的中位线,
∴DE=CF=1,
故答案为:1.
18.
【解析】
证明:∵点D,E分别是边BC,AC的中点,
∴DE∥BF,DE=AB,
∵AF=AB,
∴DE=AF,
∴四边形ADEF是平行四边形.
19.
【解析】
证明:∵点分别为的中点,
是的中位线,
∴,
∴,
在和中,,
∴,
∴.
20.
【解析】
证明:连接AC,如图所示.
∵点E是AB的中点,点F是BC的中点,
∴EF∥AC,EF=AC.
同理,可得出:HG∥AC,HG=AC,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形.
21.(1)见解析;(2)AB=AC.
(1)解:证明:在△ACD中,点O,E分别为边AC,AD中点,
∴OE为△ACD的中位线,
∴OE∥CD,OE=CD,
又∵OE=OF,
∴OF∥CD,OF=CD,
∴四边形OCDF为平行四边形;
(2)解:当AB=AC时,四边形FOCD是菱形,理由如下:
∵四边形ABCD是平行四边形,
∴AB=CD,OC=AC,
∵AB=AC,
∴AB=CD=OC,
由(1)得:四边形OCDF为平行四边形,
∴平行四边形FOCD是菱形,
故答案案为:AB=AC.
22.DF∥EG,DF=EG,证明见解析
【解析】
解:DF∥EG,DF=EG,证明如下:
连接AO,
∵BE是AC的中线,
∴E是AC的中点,
又∵G是OC的中点,
∴GE是△ACO的中位线,
∴,GE∥AO,
同理可证明DF是△ABO的中位线,
∴,DF∥AO,
∴DF∥EG,DF=EG.
23.
【解析】
证明:∵DE、DF是△ABC的中位线,
∴DE∥AB,DF∥AC,
∴四边形DEAF是平行四边形,
∵∠CAB=90°,
∴四边形DEAF是矩形,
∴EF=AD.
24.
【解析】
解:(1)∵D、E、F分别是AB、AC、BC的中点,
∴DE、DF分别是△ABC中BC边、AC边上的中位线,
∴DE∥BC,DE=BC,DF∥AC,DF=AC,
∵DE∥FC,DF∥EC,
∴四边形DECF为平行四边形,
又∵AC=BC,
∴DF=DE,
∴为菱形;
(2)∵,,
∴四边形是平行四边形,
∴与ADG面积相等的平行四边形有:
DECF,DEFB,EGCF,AEFD.
25.
【解析】
证明:如图,延长AN、AM分别交BC于点D、G.
∵BE为∠ABC的角平分线,BE⊥AG,
∴∠ABN=∠GBN,∠ANB=∠GNB=90°,
∴∠BAG=∠BGA,
∴△ABG为等腰三角形,
∴BN也为等腰三角形的中线,即AN=GN.
同理AM=DM,
∴MN为△ADG的中位线,
∴MN∥DG,
∴MN∥BC.
26.
【解析】
(1)解:四边形是正方形,
,
;
(2)①解:,,,,、、、的中点分别为、、、,
,,,,,,,;
②证明:、为、的中点,
是的中位线,
,,
同理:,,
,,
四边形是平行四边形,
,,,
,
,
平行四边形是矩形;
③解:由①得:,,,,,,,,
矩形是正方形,
,
,
,
故答案为:.
答案第8页,共9页
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
