2021-2022学年人教版数学八下17.1勾股定理的证明及简单应用 分层练课件((共21张PPT))
文档属性
| 名称 | 2021-2022学年人教版数学八下17.1勾股定理的证明及简单应用 分层练课件((共21张PPT)) |

|
|
| 格式 | ppt | ||
| 文件大小 | 781.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
勾股定理的证明及简单应用
1.在 Rt△ABC中,∠C=90°,
(1)如果a=1,b=2,求c;
(2)如果c=5,b=4,求a.
解:(1) ;
(2)
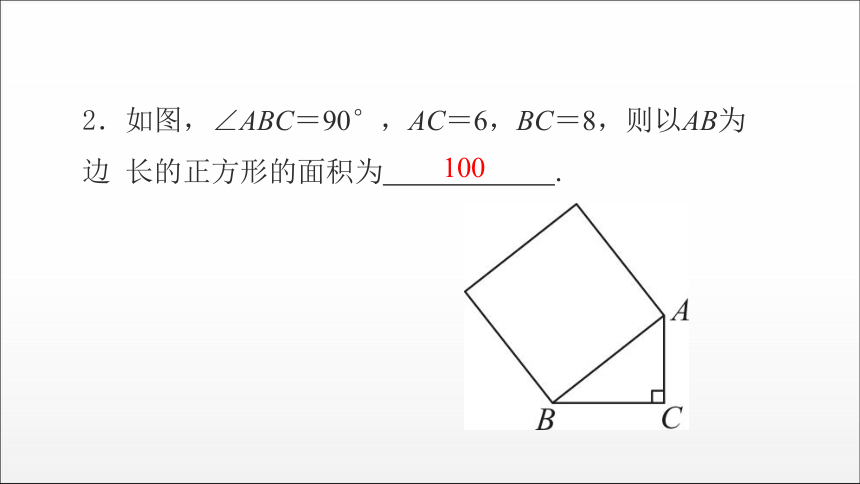
2.如图,∠ABC=90°,AC=6,BC=8,则以AB为边 长的正方形的面积为 .
100
3.如图,在 Rt△ABC中,∠C=90°,BC=5,AB=13.
求:(1)AC的长;
(2)△ABC的面积.
解:(1)
(2)
4.如图,等边△ABC的边长为4,求△ABC的高AB和面积.
解:
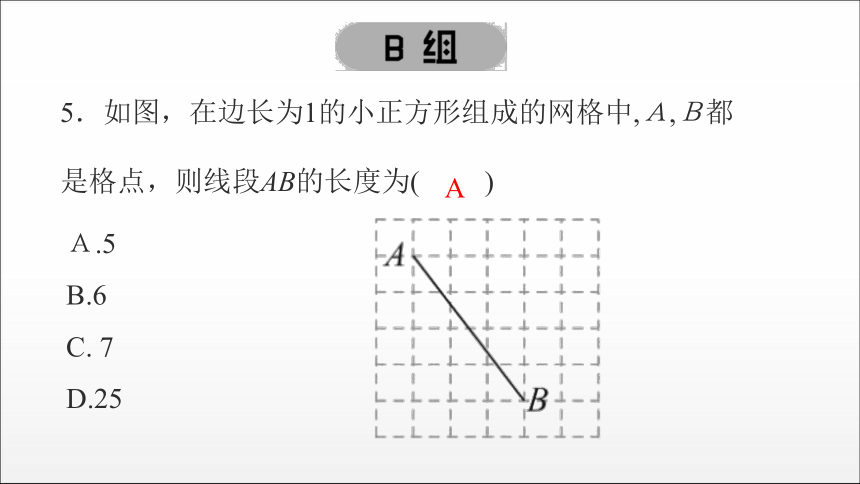
5.如图,在边长为1的小正方形组成的网格中,A,B都是格点,则线段AB的长度为( )
A.5
B.6
C. 7
D.25
A
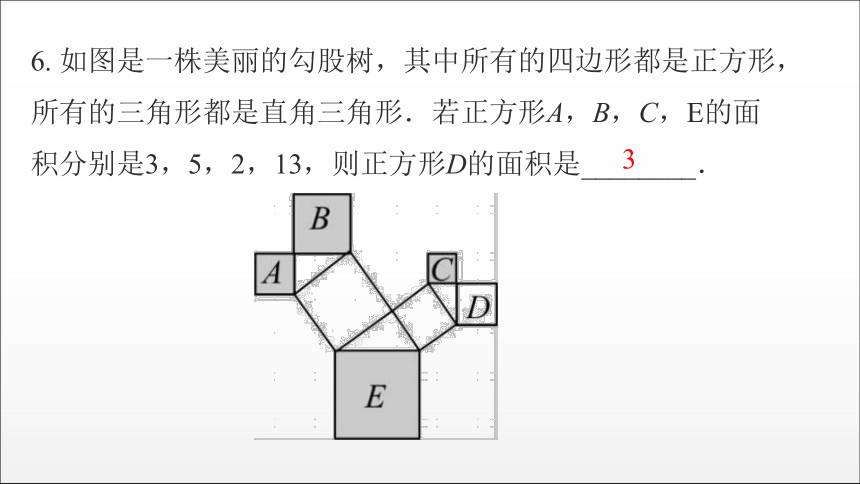
6. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,E的面积分别是3,5,2,13,则正方形D的面积是________.
3
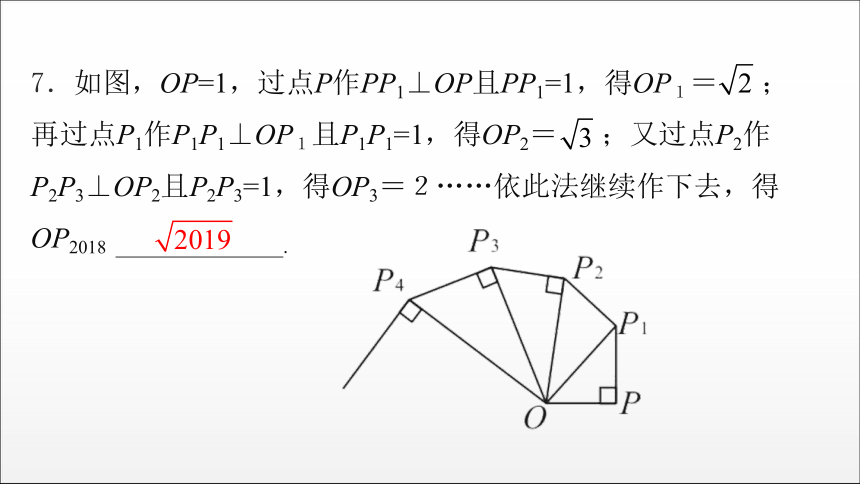
7.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1= ;再过点P1作P1P1⊥OP1且P1P1=1,得OP2= ;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2018 .
8.如图是美国总统Garfield于1876年给出的一种验证勾股定理的方法,你能利用它来验证勾股定理吗?
证明:由 BE=CF=b ,BF=CG=a,EF=GF=c
知△BEF≌△CFG , ∴∠EFB=∠FGC
∵∠FGC+∠CFG=90°,
∴∠EFB+∠CFG=90°∴∠EFG=90°
∴△EFG是等腰直角三角形
∴S△EFG=
∵∠EBF=90°,∠GCF=90°
∴BE∥CG,∴四边形BCGE是直角梯形.
∴
又∵ , ,
∴
∴
∴
谢谢!
勾股定理的应用
1.求下列各图中未知的边的长度.
(1)
(2)
解:(1)
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,AC= ,求BC的长.
解:设 BC=x,则 AB=2x
由勾股定理得(2x)2=x2+( )2
解得 x=2
所以BC的长为 2
3.如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒 0.5米的速度收绳子.问:
(1) 未开始收绳子的时候,图中绳子BC的长度是多少米?
(2) 收绳2秒后船离岸边多少米?(结果保留根号)
(1)在Rt△ABC中,∠ABC=30°,
∴BC=2AC=4(米)
(2)如图,收绳2秒后,绳子BC缩短了1米,此时绳子只有3米,即CD=3米,在Rt△ACD中,根据勾股定理得船到河岸的距离为
AD= = = (米).
即收绳2秒后船离岸边 米.
4.如图,在 Rt△ABC中,∠C=90°,D是BC边上一 点,且BD=AD=10,∠ADC=60°,求△ABC的面积.
解:∵∠C=90°,∠ADC=60°
∴∠CAD=30°, ∵BD=AD=10,
∴DC=5,AC= = , ∴BC=BD+CD=15
∴
5.如图,∠A=60°,∠B=∠D=90°,AB=2,CD=1,
求BC和AD的长.
解:延长AD与BC,两延长线交于点E,如图所示,
∵∠B=90°,∠A=60°, ∴∠E=30°
在 Rt△CDE中,CD=1, ∴ CE=2CD=2.
根据勾股定理得:DE= =
在 Rt△ABE中,AB=2, ∴ AE=2AB=4.
根据勾股定理得:BE= = .
则BC=BE-CE= , AD=AE-DE= .
6.如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
求证:AE2+AD2=2AC2.(提示:连接BD)
证明:连接BD,如图所示:
∵△ACB与△ECD都是等腰直角三角形
∴∠ECD=∠ACB=90°, ∠E=∠ADC=∠CAB=45°
EC=DC,AC=BC,AC2+BC2=AB2
∴2AC2=AB2,∠ECD-∠ACD=∠ACB-∠ACD
∴∠ACE=∠BCD
在△AEC和△BDC中
∴△AEC≌△BDC(SAS)
∴AE=BD, ∠E=∠BDC
∴∠BDC=45°,∠BDC+∠ADC=90°,即∠ADB=90°
∴AD2+BD2=AB2 ,
∴AD2+AE2=2AC2
谢谢!
勾股定理的证明及简单应用
1.在 Rt△ABC中,∠C=90°,
(1)如果a=1,b=2,求c;
(2)如果c=5,b=4,求a.
解:(1) ;
(2)
2.如图,∠ABC=90°,AC=6,BC=8,则以AB为边 长的正方形的面积为 .
100
3.如图,在 Rt△ABC中,∠C=90°,BC=5,AB=13.
求:(1)AC的长;
(2)△ABC的面积.
解:(1)
(2)
4.如图,等边△ABC的边长为4,求△ABC的高AB和面积.
解:
5.如图,在边长为1的小正方形组成的网格中,A,B都是格点,则线段AB的长度为( )
A.5
B.6
C. 7
D.25
A
6. 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,E的面积分别是3,5,2,13,则正方形D的面积是________.
3
7.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1= ;再过点P1作P1P1⊥OP1且P1P1=1,得OP2= ;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2……依此法继续作下去,得OP2018 .
8.如图是美国总统Garfield于1876年给出的一种验证勾股定理的方法,你能利用它来验证勾股定理吗?
证明:由 BE=CF=b ,BF=CG=a,EF=GF=c
知△BEF≌△CFG , ∴∠EFB=∠FGC
∵∠FGC+∠CFG=90°,
∴∠EFB+∠CFG=90°∴∠EFG=90°
∴△EFG是等腰直角三角形
∴S△EFG=
∵∠EBF=90°,∠GCF=90°
∴BE∥CG,∴四边形BCGE是直角梯形.
∴
又∵ , ,
∴
∴
∴
谢谢!
勾股定理的应用
1.求下列各图中未知的边的长度.
(1)
(2)
解:(1)
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,AC= ,求BC的长.
解:设 BC=x,则 AB=2x
由勾股定理得(2x)2=x2+( )2
解得 x=2
所以BC的长为 2
3.如图,在离水面高度(AC)为2米的岸上有人用绳子拉船靠岸,开始时绳子与水面的夹角为30°,此人以每秒 0.5米的速度收绳子.问:
(1) 未开始收绳子的时候,图中绳子BC的长度是多少米?
(2) 收绳2秒后船离岸边多少米?(结果保留根号)
(1)在Rt△ABC中,∠ABC=30°,
∴BC=2AC=4(米)
(2)如图,收绳2秒后,绳子BC缩短了1米,此时绳子只有3米,即CD=3米,在Rt△ACD中,根据勾股定理得船到河岸的距离为
AD= = = (米).
即收绳2秒后船离岸边 米.
4.如图,在 Rt△ABC中,∠C=90°,D是BC边上一 点,且BD=AD=10,∠ADC=60°,求△ABC的面积.
解:∵∠C=90°,∠ADC=60°
∴∠CAD=30°, ∵BD=AD=10,
∴DC=5,AC= = , ∴BC=BD+CD=15
∴
5.如图,∠A=60°,∠B=∠D=90°,AB=2,CD=1,
求BC和AD的长.
解:延长AD与BC,两延长线交于点E,如图所示,
∵∠B=90°,∠A=60°, ∴∠E=30°
在 Rt△CDE中,CD=1, ∴ CE=2CD=2.
根据勾股定理得:DE= =
在 Rt△ABE中,AB=2, ∴ AE=2AB=4.
根据勾股定理得:BE= = .
则BC=BE-CE= , AD=AE-DE= .
6.如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上.
求证:AE2+AD2=2AC2.(提示:连接BD)
证明:连接BD,如图所示:
∵△ACB与△ECD都是等腰直角三角形
∴∠ECD=∠ACB=90°, ∠E=∠ADC=∠CAB=45°
EC=DC,AC=BC,AC2+BC2=AB2
∴2AC2=AB2,∠ECD-∠ACD=∠ACB-∠ACD
∴∠ACE=∠BCD
在△AEC和△BDC中
∴△AEC≌△BDC(SAS)
∴AE=BD, ∠E=∠BDC
∴∠BDC=45°,∠BDC+∠ADC=90°,即∠ADB=90°
∴AD2+BD2=AB2 ,
∴AD2+AE2=2AC2
谢谢!
