2021-2022学年人教版八年级数学下册17.1勾股定理 课件(共41张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级数学下册17.1勾股定理 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 772.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 20:04:02 | ||
图片预览



文档简介
(共41张PPT)
勾股定理
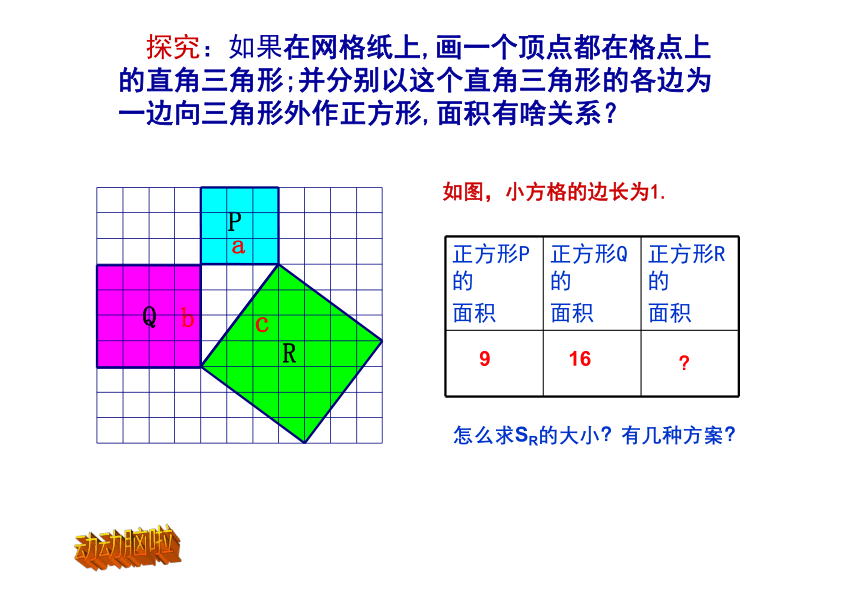
探究:如果在网格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方形,面积有啥关系?
正方形P的 面积 正方形Q的 面积 正方形R的
面积
9
16
?
怎么求SR的大小?有几种方案?
动动脑啦
如图,小方格的边长为1.
P
Q
R
a
c
b
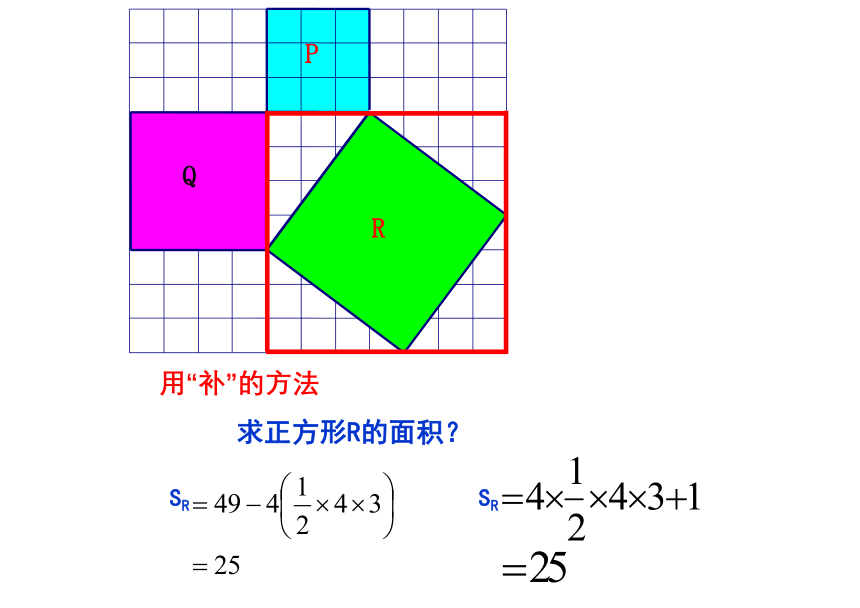
求正方形R的面积?
用“补”的方法
P
Q
C
R
SR
SR
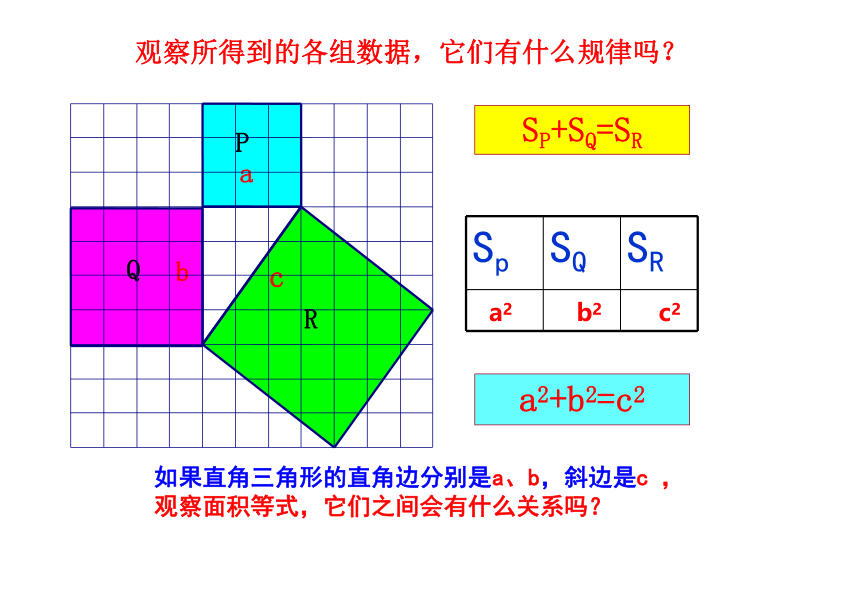
SP+SQ=SR
如果直角三角形的直角边分别是a、b,斜边是c ,观察面积等式,它们之间会有什么关系吗?
a2+b2=c2
P
Q
R
a
c
b
Sp SQ SR
观察所得到的各组数据,它们有什么规律吗?
a2
b2
c2
勾
股
勾
股
弦
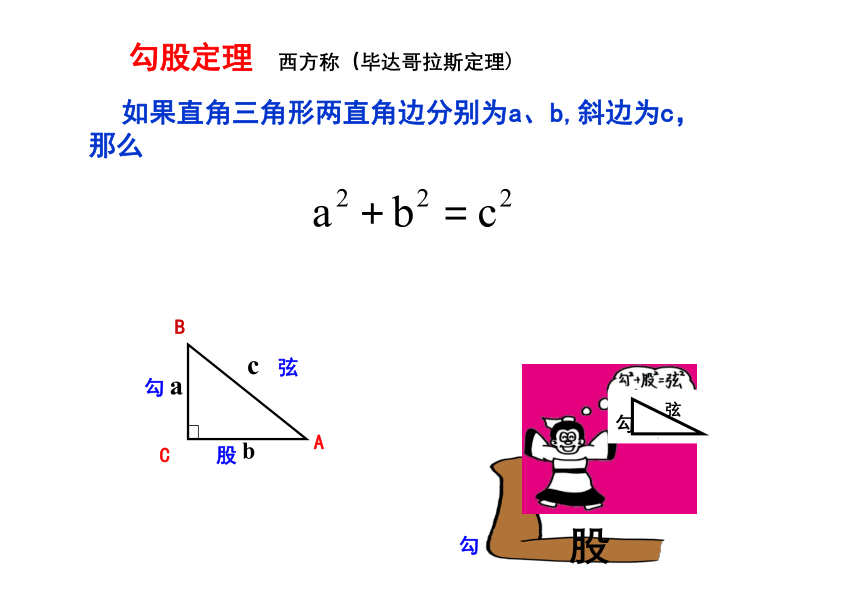
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形两直角边的平方和等于斜边的平方
西方称(毕达哥拉斯定理)
A
C
B
弦
勾
股
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾股世界
数学史
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
在西方,一般认为这个定理是毕达哥拉斯发现的,所以人们称这个定理为毕达哥拉斯定理。
c
a
b
c
a
b
c
a
b
c
a
b
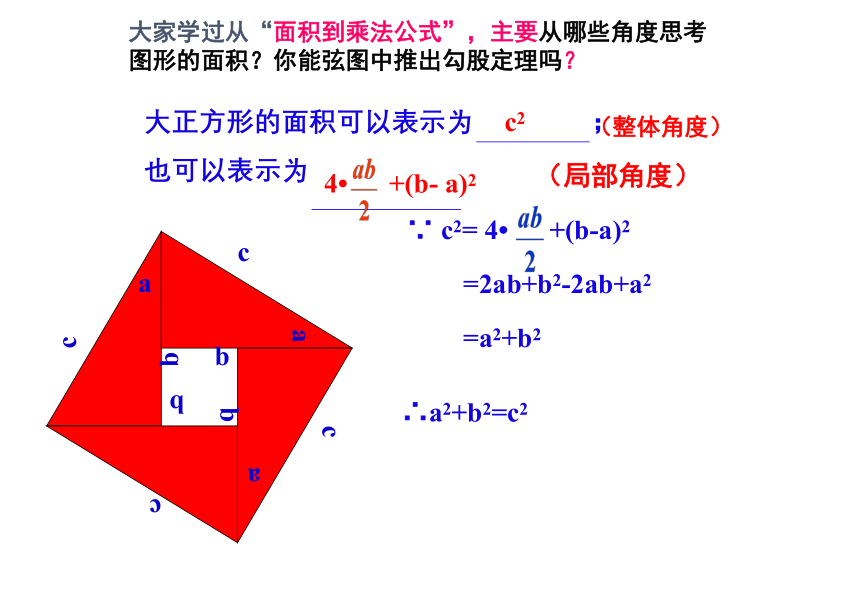
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 +(b- a)2
∵ c2= 4 +(b-a)2
大家学过从“面积到乘法公式”,主要从哪些角度思考图形的面积?你能弦图中推出勾股定理吗?
(整体角度)
(局部角度)
c
a
b
c
a
b
c
a
b
c
a
b
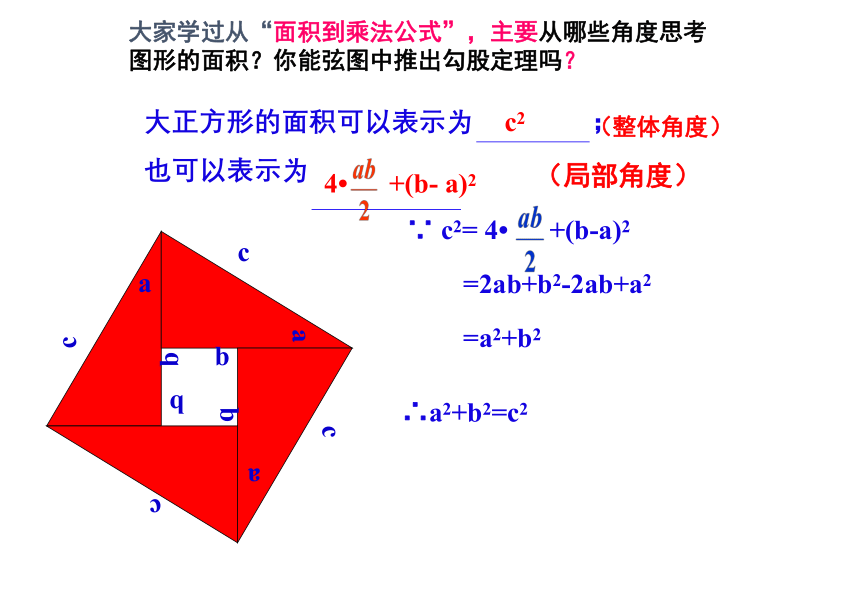
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 +(b- a)2
∵ c2= 4 +(b-a)2
大家学过从“面积到乘法公式”,主要从哪些角度思考图形的面积?你能弦图中推出勾股定理吗?
(整体角度)
(局部角度)
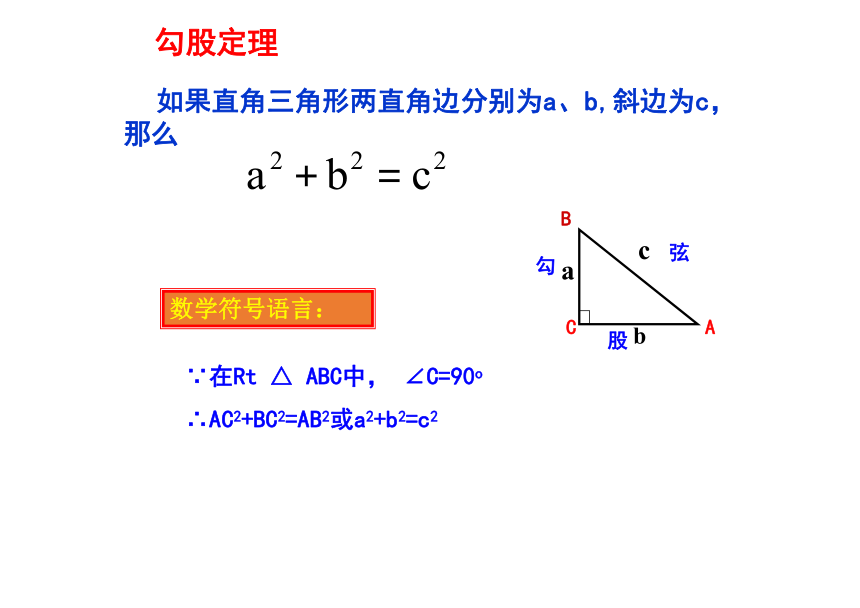
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
A
C
B
数学符号语言:
∵在Rt △ ABC中, ∠C=90o
∴AC2+BC2=AB2或a2+b2=c2
弦
勾
股
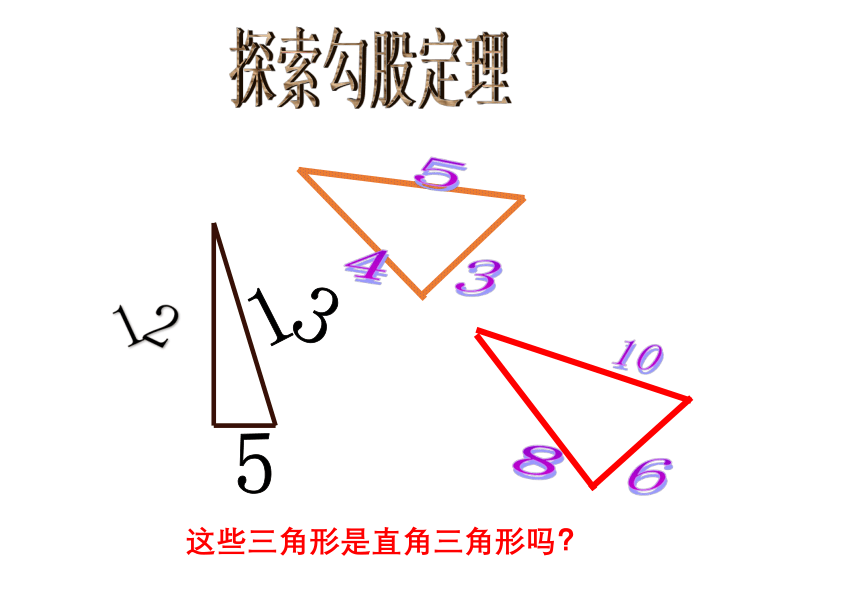
探索勾股定理
5
13
3
4
12
5
10
6
8
这些三角形是直角三角形吗?
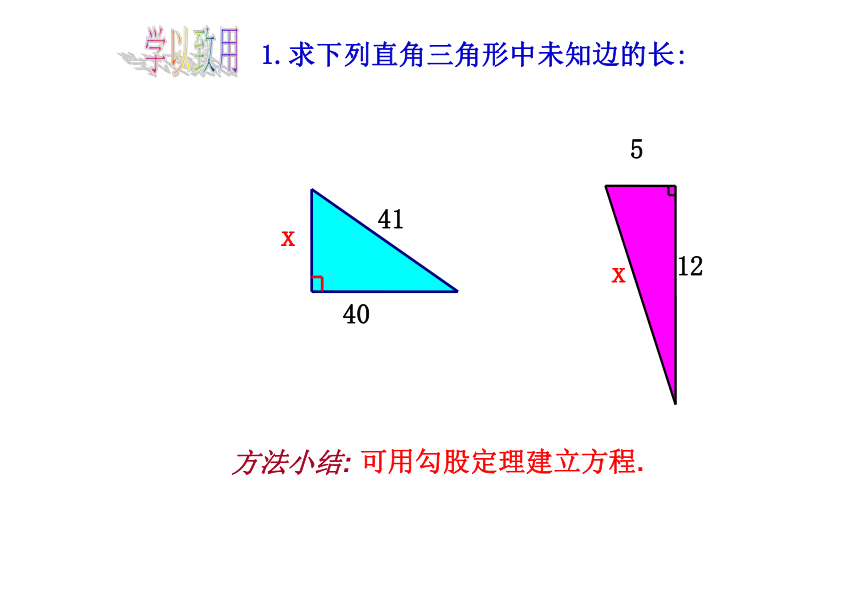
1.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
40
x
41
12
5
x
学以致用
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕长只有58厘米和宽46厘米,他认为是售货员搞错了。你同意他的看法吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度,对角线怎么求?
例
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
解:∵
议一议
∴荧屏对角线大约为74厘米
46
58
例2、已知△ABC中, ∠C= 90o,BC= a ,AC= b ,AB=c
已知: a=3, b=4, 求 c;
已知: a =6 , c =8, 求 c;
(3)已知:c=15 , a : b = 3 : 4,求 a ,b.
(4)若假设 BC=ma,AC=mb,m为正整数
求 c;
C
A
B
例2、已知△ABC中, ∠C= 90o,BC= a ,AC= b ,AB=c
已知: a=3, b=4, 求 c; c=5
已知: a =6 , c =8, 求 c; c=5
(3)已知:c=15 , a : b = 3 : 4,求 a ,b.
a=9 ,b=12
(4)若假设 BC=ma,AC=mb,m为正整数,求AB;
AB=mc
C
A
B
1、已知:Rt△ABC中,AB=4,AC=3,则BC是 .
巩固练习
2.有两棵树,一颗高8m,另一棵2m,两树相距8m,一只小鸟从一棵树梢飞到另一棵树梢,至少飞了多少米?
2.有两棵树,一颗高8m,另一棵2m,两树相距8m,一只小鸟从一棵树梢飞到另一棵树梢,至少飞了多少米?
A
B
C
解: AC=8-2=6, BC=8,
AB2=AC2+BC2=36+64=100
∴AB=10
80
60
35
20
B
A
3. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
80
60
35
20
B
A
3. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
C
解: AC=60-35=25,
BC=80-20=60,
AB2=AC2+BC2=625+3600=4225
∴AB=65
A
C
O
B
D
4.一个5m长的梯子AB,斜靠在一竖直的墙AO上,
这时AO的距离为4m,如果梯子的顶端A沿墙
下滑1m,那么梯子底端B也外移多少
经典例题
A
C
O
B
D
4.一个5m长的梯子AB,斜靠在一竖直的墙AO上,
这时AO的距离为4m,如果梯子的顶端A沿墙
下滑1m,那么梯子底端B也外移多少
经典例题
解: ∵AO=4, AB=5
∴OB=3,
∵AC=1, OC=3 ,CD=5
∴OD=4,
∴BD=1
5.已知:△ABC,AB=AC=17,BC=16.
(1)求高AD的长;
(2)求S△ABC .
A
B
C
D
17
解: ∵AB=AC ,AD为高,BC=16,
∴BD=8
∴AD2=AB2-BD2=172-82=225
∴AD=15
0
1
2
3
-1
-2
-3
如图,AB=ACA,则数轴上点C所表示的数为________.
8.如果Rt△的两直角边长分别为n2-1,2n(n>1),那么它的斜边长是( )
A、2n B、n+1 C、n -1 D、n +1
经典例题
D
3、一个直立的火柴盒在桌面上倒下,人们发现勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A'B'C'D'的位置,连接CC,设AB=a,BC=b,AC=c,用四边形BCC'D'的面积证明勾股定理:a2+b2=c2.
9.如图,Rt△ABC中,两直角边AC=6 ,BC=8 ,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等( )
A、2 B、3 C、4 D、5
经典例题
B
1.如图,一只蚂蚁从边长为5的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬的最短路线的长为 _______
经典例题
A
B
2.如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
A
B
·
A
B ·
8
2×3×2
6
C
10
5
4
3
2
1
观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
49
7.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A、B、C、D的面积的和是_____
经典例题
49
△ABC三边a,b,c为边向外作正方形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
A
B
C
a
b
c
S1
S2
S3
B
S
S
S
C
B
A
△ABC三边a,b,c,以三边为边长分别作等边三角形,若S1+S2=S3成立,则△ABC
是直角三角形吗?
1、如图,直线1上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A、4 B、6 C、16 D、55
a
b
c
巩固练习
C
2.如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,
求:(1)FC的长;(2)EF的长.
A
D
C
B
E
F
经典例题
2.如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,
求:(1)FC的长;(2)EF的长.
A
D
C
B
E
F
经典例题
解:由折叠得:AF=AD=BC=10,∵AB=8,
∴BF=6,
∴CF=BC=BF=10-6=4
设EF=x,则DE=x,CE=8-x,
∵∠C=90°,
∴CF2+CE2=EF2
∴42+(8-x)2=x2
解得 x=5
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC。已知AB=5,DE=1,BD=8,
求AC+CE的最小值
拓展提优
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC。已知AB=5,DE=1,BD=8,
求AC+CE的最小值
拓展提优
解: 作点A关于BD得对称点H,
则 AC+CE=CH+CE,
当C,E,H三点共线时,和最小为EH。
AB=BH=5,EM=ED+DM=6,MH=BD=8
∴由勾股定理得 :EH=10
∴AC+CE的最小值为10.
H
M
13.如图,海中有一小岛A,在该岛周围10海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45 的B处,往东航行20海里后达到该岛南偏西30 的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?
拓展提优
13.如图,海中有一小岛A,在该岛周围20海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45 的B处,往东航行10海里后达到该岛南偏西30 的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?
拓展提优
D
解,作AD⊥BC于D,
设AD=x, ∵∠BAD=45°,∠CAD=30°,
∴BD=AD=x,
∵BD-CD=BC
因为AD>20,所以不会有4触礁危险。
勾股定理
探究:如果在网格纸上,画一个顶点都在格点上的直角三角形;并分别以这个直角三角形的各边为一边向三角形外作正方形,面积有啥关系?
正方形P的 面积 正方形Q的 面积 正方形R的
面积
9
16
?
怎么求SR的大小?有几种方案?
动动脑啦
如图,小方格的边长为1.
P
Q
R
a
c
b
求正方形R的面积?
用“补”的方法
P
Q
C
R
SR
SR
SP+SQ=SR
如果直角三角形的直角边分别是a、b,斜边是c ,观察面积等式,它们之间会有什么关系吗?
a2+b2=c2
P
Q
R
a
c
b
Sp SQ SR
观察所得到的各组数据,它们有什么规律吗?
a2
b2
c2
勾
股
勾
股
弦
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
直角三角形两直角边的平方和等于斜边的平方
西方称(毕达哥拉斯定理)
A
C
B
弦
勾
股
我国是最早了解勾股定理的国家之一。早在三千多年前,周朝数学家商高就提出,将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”,它被记载于我国古代著名的数学著作《周髀算经》中。
勾股世界
数学史
1945年,人们在研究古巴比伦人遗留下的一块数学泥板时,惊讶地发现上面竟然刻有15组能构成直角三角形三边的数,其年代远在商高之前。
在西方,一般认为这个定理是毕达哥拉斯发现的,所以人们称这个定理为毕达哥拉斯定理。
c
a
b
c
a
b
c
a
b
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 +(b- a)2
∵ c2= 4 +(b-a)2
大家学过从“面积到乘法公式”,主要从哪些角度思考图形的面积?你能弦图中推出勾股定理吗?
(整体角度)
(局部角度)
c
a
b
c
a
b
c
a
b
c
a
b
=2ab+b2-2ab+a2
=a2+b2
∴a2+b2=c2
大正方形的面积可以表示为 ;
也可以表示为
c2
4 +(b- a)2
∵ c2= 4 +(b-a)2
大家学过从“面积到乘法公式”,主要从哪些角度思考图形的面积?你能弦图中推出勾股定理吗?
(整体角度)
(局部角度)
勾股定理
如果直角三角形两直角边分别为a、b,斜边为c,那么
a
b
c
A
C
B
数学符号语言:
∵在Rt △ ABC中, ∠C=90o
∴AC2+BC2=AB2或a2+b2=c2
弦
勾
股
探索勾股定理
5
13
3
4
12
5
10
6
8
这些三角形是直角三角形吗?
1.求下列直角三角形中未知边的长:
可用勾股定理建立方程.
方法小结:
40
x
41
12
5
x
学以致用
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕长只有58厘米和宽46厘米,他认为是售货员搞错了。你同意他的看法吗?
我们通常所说的29英寸或74厘米的电视机,是指其荧屏对角线的长度,对角线怎么求?
例
小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
解:∵
议一议
∴荧屏对角线大约为74厘米
46
58
例2、已知△ABC中, ∠C= 90o,BC= a ,AC= b ,AB=c
已知: a=3, b=4, 求 c;
已知: a =6 , c =8, 求 c;
(3)已知:c=15 , a : b = 3 : 4,求 a ,b.
(4)若假设 BC=ma,AC=mb,m为正整数
求 c;
C
A
B
例2、已知△ABC中, ∠C= 90o,BC= a ,AC= b ,AB=c
已知: a=3, b=4, 求 c; c=5
已知: a =6 , c =8, 求 c; c=5
(3)已知:c=15 , a : b = 3 : 4,求 a ,b.
a=9 ,b=12
(4)若假设 BC=ma,AC=mb,m为正整数,求AB;
AB=mc
C
A
B
1、已知:Rt△ABC中,AB=4,AC=3,则BC是 .
巩固练习
2.有两棵树,一颗高8m,另一棵2m,两树相距8m,一只小鸟从一棵树梢飞到另一棵树梢,至少飞了多少米?
2.有两棵树,一颗高8m,另一棵2m,两树相距8m,一只小鸟从一棵树梢飞到另一棵树梢,至少飞了多少米?
A
B
C
解: AC=8-2=6, BC=8,
AB2=AC2+BC2=36+64=100
∴AB=10
80
60
35
20
B
A
3. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
80
60
35
20
B
A
3. 如图所示是某机械零件的平面图,尺寸如图所示, 求两孔中心A, B之间的距离.(单位:毫米)
C
解: AC=60-35=25,
BC=80-20=60,
AB2=AC2+BC2=625+3600=4225
∴AB=65
A
C
O
B
D
4.一个5m长的梯子AB,斜靠在一竖直的墙AO上,
这时AO的距离为4m,如果梯子的顶端A沿墙
下滑1m,那么梯子底端B也外移多少
经典例题
A
C
O
B
D
4.一个5m长的梯子AB,斜靠在一竖直的墙AO上,
这时AO的距离为4m,如果梯子的顶端A沿墙
下滑1m,那么梯子底端B也外移多少
经典例题
解: ∵AO=4, AB=5
∴OB=3,
∵AC=1, OC=3 ,CD=5
∴OD=4,
∴BD=1
5.已知:△ABC,AB=AC=17,BC=16.
(1)求高AD的长;
(2)求S△ABC .
A
B
C
D
17
解: ∵AB=AC ,AD为高,BC=16,
∴BD=8
∴AD2=AB2-BD2=172-82=225
∴AD=15
0
1
2
3
-1
-2
-3
如图,AB=ACA,则数轴上点C所表示的数为________.
8.如果Rt△的两直角边长分别为n2-1,2n(n>1),那么它的斜边长是( )
A、2n B、n+1 C、n -1 D、n +1
经典例题
D
3、一个直立的火柴盒在桌面上倒下,人们发现勾股定理的一种新的证明方法,如图所示,火柴盒的一个侧面ABCD倒下到A'B'C'D'的位置,连接CC,设AB=a,BC=b,AC=c,用四边形BCC'D'的面积证明勾股定理:a2+b2=c2.
9.如图,Rt△ABC中,两直角边AC=6 ,BC=8 ,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等( )
A、2 B、3 C、4 D、5
经典例题
B
1.如图,一只蚂蚁从边长为5的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬的最短路线的长为 _______
经典例题
A
B
2.如图是 一大厦的柱子,它是圆柱形的 ,它的高是8米,底面半径是2米,一只壁虎在A点,想要吃到B点的昆虫,它爬行的最短距离 是多少?(圆周率取3)
A
B
·
A
B ·
8
2×3×2
6
C
10
5
4
3
2
1
观察下列图形,正方形1的边长为7,则
正方形2、3、4、5的面积之和为多少?
49
7.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形A、B、C、D的面积的和是_____
经典例题
49
△ABC三边a,b,c为边向外作正方形,以三边为直径作半圆,若S1+S2=S3成立,则△ABC
是直角三角形吗?
A
C
a
b
c
S1
S2
S3
A
B
C
a
b
c
S1
S2
S3
B
S
S
S
C
B
A
△ABC三边a,b,c,以三边为边长分别作等边三角形,若S1+S2=S3成立,则△ABC
是直角三角形吗?
1、如图,直线1上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )
A、4 B、6 C、16 D、55
a
b
c
巩固练习
C
2.如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,
求:(1)FC的长;(2)EF的长.
A
D
C
B
E
F
经典例题
2.如图,折叠长方形一边AD,点D落在BC边的点F处,BC=10cm,AB=8cm,
求:(1)FC的长;(2)EF的长.
A
D
C
B
E
F
经典例题
解:由折叠得:AF=AD=BC=10,∵AB=8,
∴BF=6,
∴CF=BC=BF=10-6=4
设EF=x,则DE=x,CE=8-x,
∵∠C=90°,
∴CF2+CE2=EF2
∴42+(8-x)2=x2
解得 x=5
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC。已知AB=5,DE=1,BD=8,
求AC+CE的最小值
拓展提优
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC。已知AB=5,DE=1,BD=8,
求AC+CE的最小值
拓展提优
解: 作点A关于BD得对称点H,
则 AC+CE=CH+CE,
当C,E,H三点共线时,和最小为EH。
AB=BH=5,EM=ED+DM=6,MH=BD=8
∴由勾股定理得 :EH=10
∴AC+CE的最小值为10.
H
M
13.如图,海中有一小岛A,在该岛周围10海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45 的B处,往东航行20海里后达到该岛南偏西30 的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?
拓展提优
13.如图,海中有一小岛A,在该岛周围20海里内有暗礁,今有货船由西向东航行,开始在A岛南偏西45 的B处,往东航行10海里后达到该岛南偏西30 的C处,之后继续向东航行,你认为货船继续向东航行会有触礁的危险吗?
拓展提优
D
解,作AD⊥BC于D,
设AD=x, ∵∠BAD=45°,∠CAD=30°,
∴BD=AD=x,
∵BD-CD=BC
因为AD>20,所以不会有4触礁危险。
