2021--2022学年人教版八年级数学下册17.1勾股定理 课件(共22张PPT)
文档属性
| 名称 | 2021--2022学年人教版八年级数学下册17.1勾股定理 课件(共22张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1018.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 20:05:27 | ||
图片预览



文档简介
(共22张PPT)
17.1.1 勾股定理
一、情境引入
会标中央的图案是赵爽弦图,它与“勾股定理”有关,数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号.
2002年世界数学家大会在我国北京召开,下图是本届数学家大会的会标:
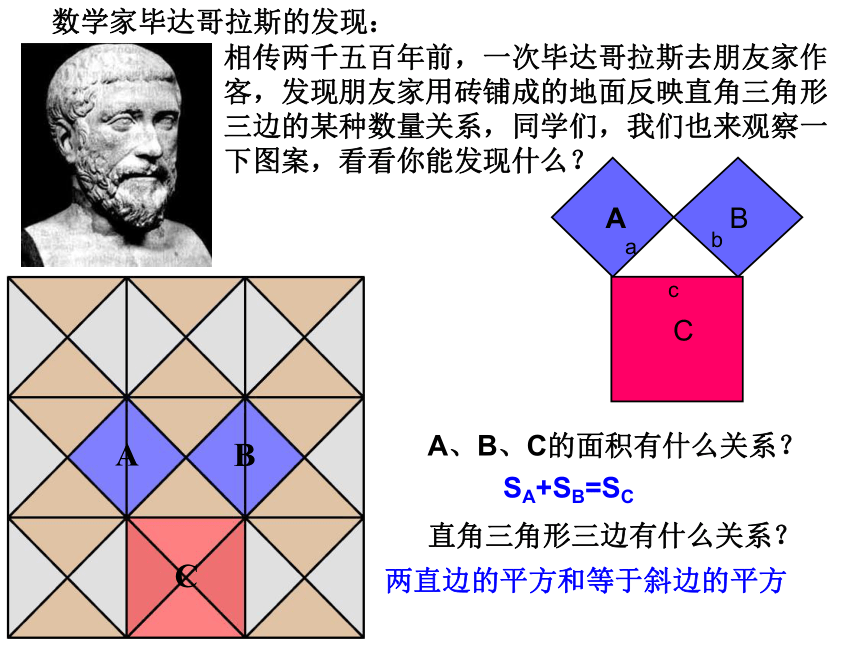
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
B
A
C
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察一下图案,看看你能发现什么?
b
a
c
A
B
C
A
B
C
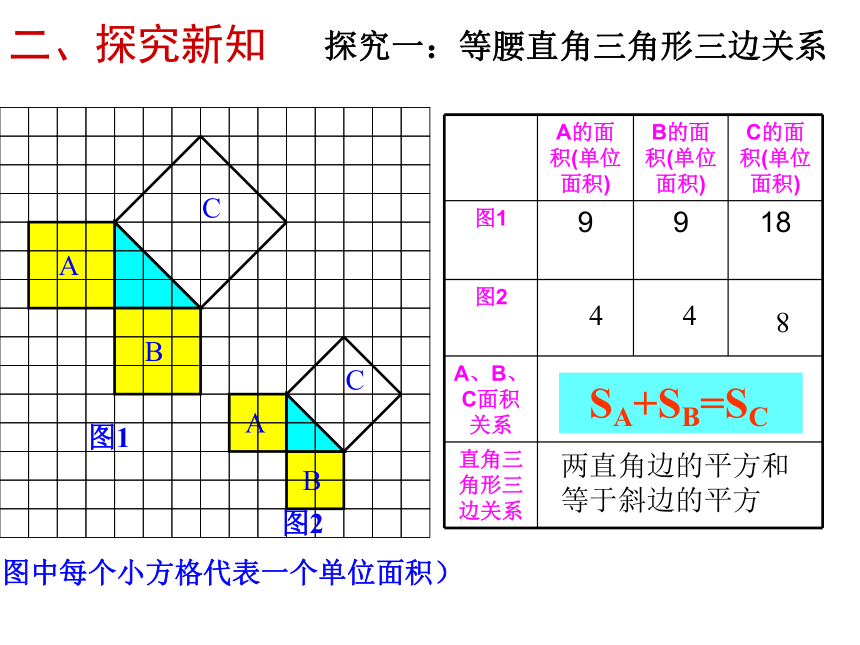
(图中每个小方格代表一个单位面积)
图1
图2
SA+SB=SC
直角三角形三边关系
A、B、C面积关系
图2
18
9
9
图1
C的面积(单位面积)
B的面积(单位面积)
A的面积(单位面积)
4
4
8
两直角边的平方和
等于斜边的平方
探究一:等腰直角三角形三边关系
二、探究新知
A
B
C
图3
A
B
C
图4
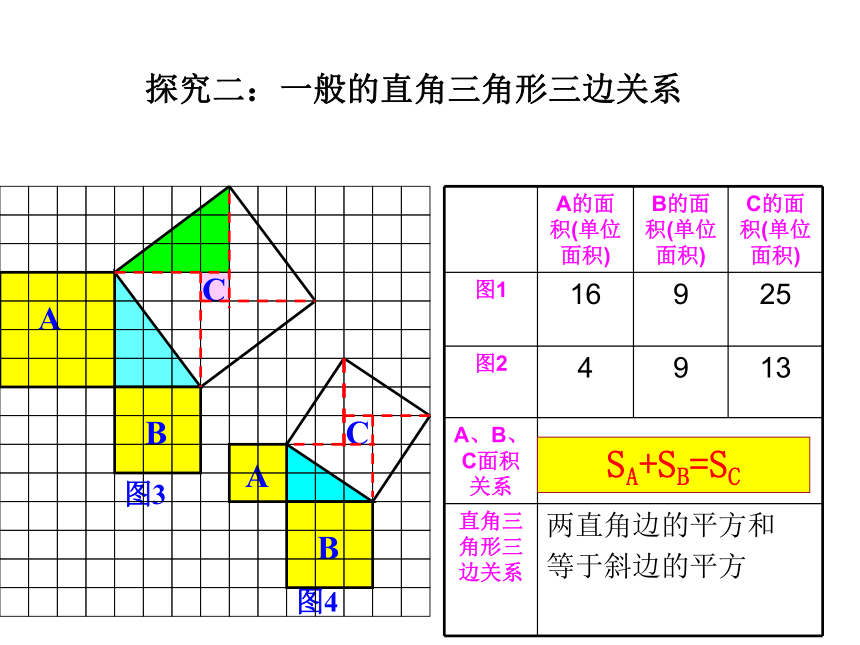
探究二:一般的直角三角形三边关系
两直角边的平方和
等于斜边的平方
直角三角形三边关系
A、B、C面积关系
13
9
4
图2
25
9
16
图1
C的面积(单位面积)
B的面积(单位面积)
A的面积(单位面积)
SA+SB=SC
A
B
C
a
c
b
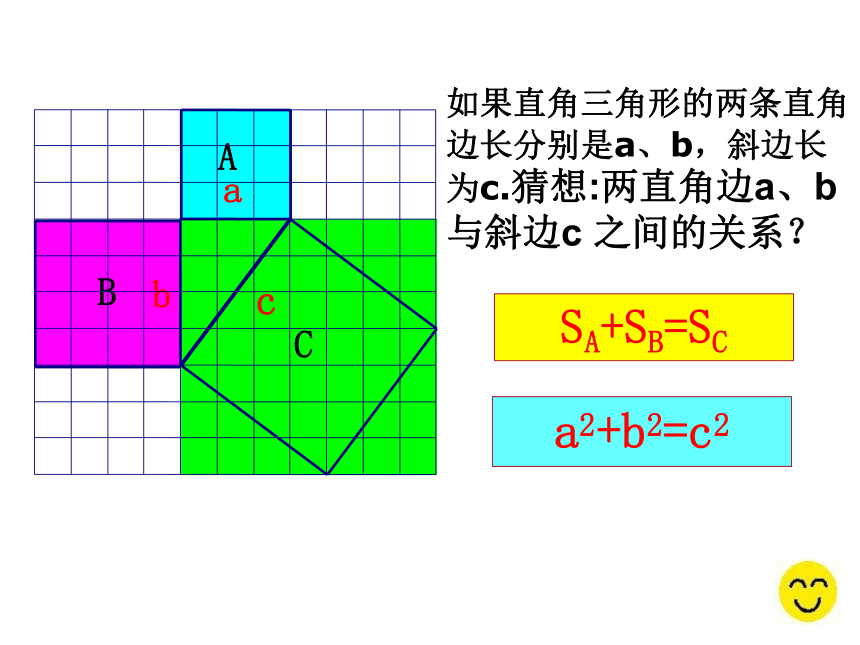
SA+SB=SC
如果直角三角形的两条直角边长分别是a、b,斜边长为c.猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
直角三角形的两条直角边的平方和等于斜边的平方.
三、得出猜想
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
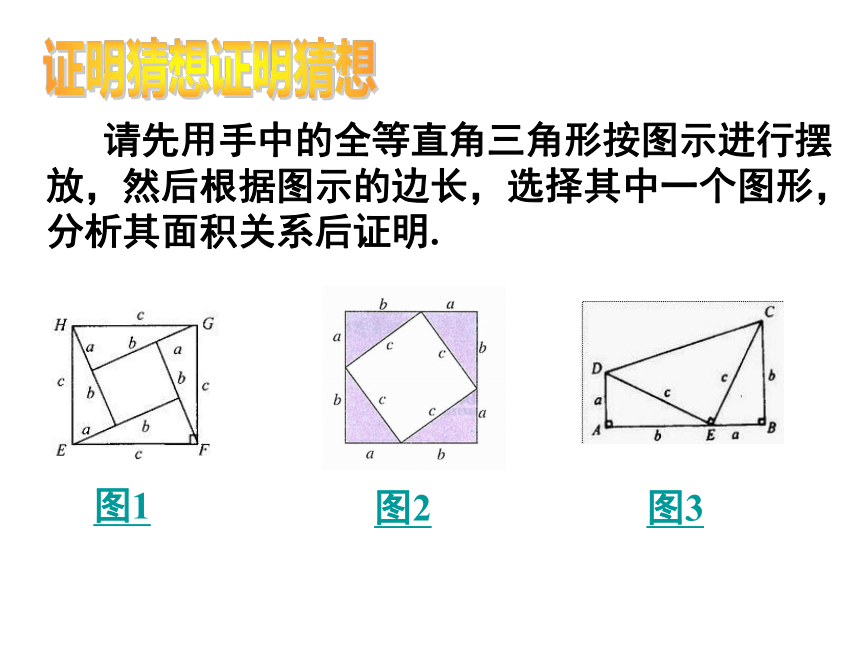
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
证明猜想
图1
图2
图3
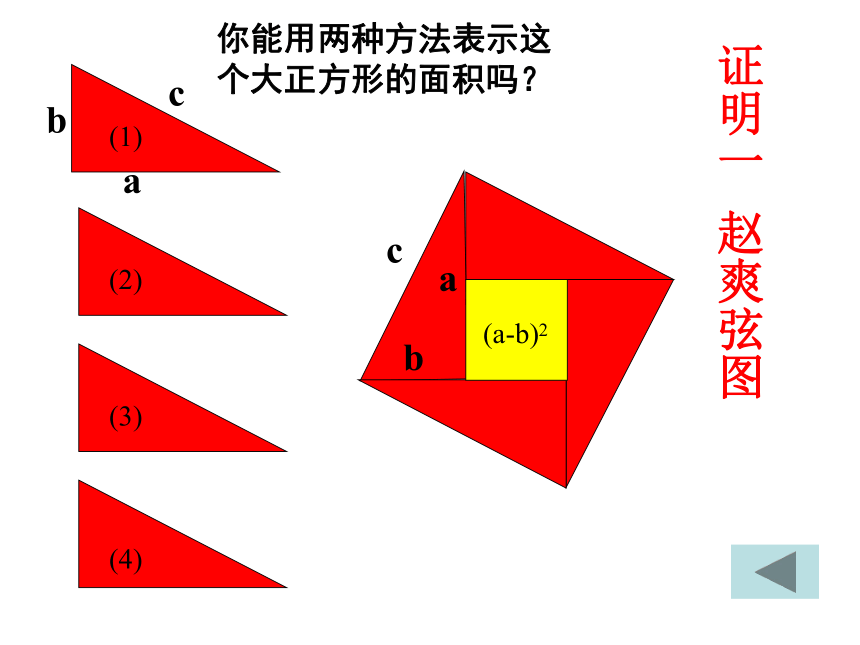
证明一 赵爽弦图
a
b
(1)
(2)
(3)
(4)
c
你能用两种方法表示这个大正方形的面积吗?
b
(a-b)2
(a-b)2
a
b
c
如果直角三角形两直角边分别为a、b,
斜边为c,那么
文字语言:直角三角形两直角边的平方和
等于斜边的平方.
a
b
c
几何语言: Rt△ABC中,
∵ ∠C=90°
∴ a2 + b2 = c2
勾股定理:
1.成立条件: 在直角三角中;
3.作用:求直角三角形某边长,
或者求某些正方形的面积。
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
(注意:哪条边是斜边)
求下列图中的SA和SB 的值.
①
81
144
SA
SB
②
做一做
144
169
SA=225
SB=25
比一比看谁算得又快又准!
求下列直角三角形中未知边的长x:
8
x
17
16
20
x
做一做
X=15
X=12
①
②
1. 已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
小试身手
2. 在Rt△ABC中,∠B=90°,a=3,c=4,求b.
3、在Rt△ABC中, ∠C=90°, a=6, a:b=3:4,求b和c.
课堂小结
(1)勾股定理的内容是什么?它有什么作用?
(2)在探究勾股定理的过程中,我们经历了怎样的探究过程?
老师的叮嘱:一个定理:勾股定理
两种思想:由特殊到一般;数形结合。
三种证法:赵爽弦图证法;毕达哥拉斯证法;总统证法。
课后作业
1.整理课堂中所提到的勾股定理的证明方法;
2.通过上网等查找有关勾股定理的有关史料、趣事及其他证明方法.
3. 课本28页第1、2、3题.
祝同学们学习进步!
感受数学文化
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究,或到网上查阅勾股
定理的相关资料.
c
b
a
(
b
-
a
)
2
黄实
朱实
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
美国第二十任总统加菲尔德的证法在数学史上被传为佳话 .
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法.
有趣的总统证法
b
c
a
b
c
a
A
B
C
D
结论:
S1+S2+S3+S4
=S5+S6
=S7
1
1
数学的和谐美
17.1.1 勾股定理
一、情境引入
会标中央的图案是赵爽弦图,它与“勾股定理”有关,数学家曾建议用“勾股定理”的图来作为与“外星人”联系的信号.
2002年世界数学家大会在我国北京召开,下图是本届数学家大会的会标:
数学家毕达哥拉斯的发现:
A、B、C的面积有什么关系?
直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
A
B
C
B
A
C
相传两千五百年前,一次毕达哥拉斯去朋友家作客,发现朋友家用砖铺成的地面反映直角三角形三边的某种数量关系,同学们,我们也来观察一下图案,看看你能发现什么?
b
a
c
A
B
C
A
B
C
(图中每个小方格代表一个单位面积)
图1
图2
SA+SB=SC
直角三角形三边关系
A、B、C面积关系
图2
18
9
9
图1
C的面积(单位面积)
B的面积(单位面积)
A的面积(单位面积)
4
4
8
两直角边的平方和
等于斜边的平方
探究一:等腰直角三角形三边关系
二、探究新知
A
B
C
图3
A
B
C
图4
探究二:一般的直角三角形三边关系
两直角边的平方和
等于斜边的平方
直角三角形三边关系
A、B、C面积关系
13
9
4
图2
25
9
16
图1
C的面积(单位面积)
B的面积(单位面积)
A的面积(单位面积)
SA+SB=SC
A
B
C
a
c
b
SA+SB=SC
如果直角三角形的两条直角边长分别是a、b,斜边长为c.猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
直角三角形的两条直角边的平方和等于斜边的平方.
三、得出猜想
如图,在Rt△ABC中,∠C=90°,∠A、∠B和∠C所对的三条边分别是a、b、c.
求证:
请先用手中的全等直角三角形按图示进行摆放,然后根据图示的边长,选择其中一个图形,分析其面积关系后证明.
证明猜想
图1
图2
图3
证明一 赵爽弦图
a
b
(1)
(2)
(3)
(4)
c
你能用两种方法表示这个大正方形的面积吗?
b
(a-b)2
(a-b)2
a
b
c
如果直角三角形两直角边分别为a、b,
斜边为c,那么
文字语言:直角三角形两直角边的平方和
等于斜边的平方.
a
b
c
几何语言: Rt△ABC中,
∵ ∠C=90°
∴ a2 + b2 = c2
勾股定理:
1.成立条件: 在直角三角中;
3.作用:求直角三角形某边长,
或者求某些正方形的面积。
2.公式变形:
a
b
c
如果直角三角形两直角边长分别为a、b,斜边长为c,那么
勾 股 定 理
(注意:哪条边是斜边)
求下列图中的SA和SB 的值.
①
81
144
SA
SB
②
做一做
144
169
SA=225
SB=25
比一比看谁算得又快又准!
求下列直角三角形中未知边的长x:
8
x
17
16
20
x
做一做
X=15
X=12
①
②
1. 已知Rt△ABC中,∠C=90°,若a=2,c=5,求b.
小试身手
2. 在Rt△ABC中,∠B=90°,a=3,c=4,求b.
3、在Rt△ABC中, ∠C=90°, a=6, a:b=3:4,求b和c.
课堂小结
(1)勾股定理的内容是什么?它有什么作用?
(2)在探究勾股定理的过程中,我们经历了怎样的探究过程?
老师的叮嘱:一个定理:勾股定理
两种思想:由特殊到一般;数形结合。
三种证法:赵爽弦图证法;毕达哥拉斯证法;总统证法。
课后作业
1.整理课堂中所提到的勾股定理的证明方法;
2.通过上网等查找有关勾股定理的有关史料、趣事及其他证明方法.
3. 课本28页第1、2、3题.
祝同学们学习进步!
感受数学文化
这个图案是公元3世纪我国汉代的赵爽在注解《周
髀算经》时给出的,人们称它为“赵爽弦图”.赵爽根
据此图指出:四个全等的直角三角形(红色)可以如图
围成一个大正方形,中间的部分是一个小正方形 (黄
色).勾股定理在数学发展中起
到了重大的作用,其证明方法据
说有400 多种,有兴趣的同学可
以继续研究,或到网上查阅勾股
定理的相关资料.
c
b
a
(
b
-
a
)
2
黄实
朱实
毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年.希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了.
美国第二十任总统加菲尔德的证法在数学史上被传为佳话 .
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法.
有趣的总统证法
b
c
a
b
c
a
A
B
C
D
结论:
S1+S2+S3+S4
=S5+S6
=S7
1
1
数学的和谐美
