2021-2022学年人教版八年级下册17.1勾股定理的验证及应用 课件(共15张PPT)
文档属性
| 名称 | 2021-2022学年人教版八年级下册17.1勾股定理的验证及应用 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 813.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 20:07:38 | ||
图片预览



文档简介
(共15张PPT)
勾股定理的验证及应用
b
a
c
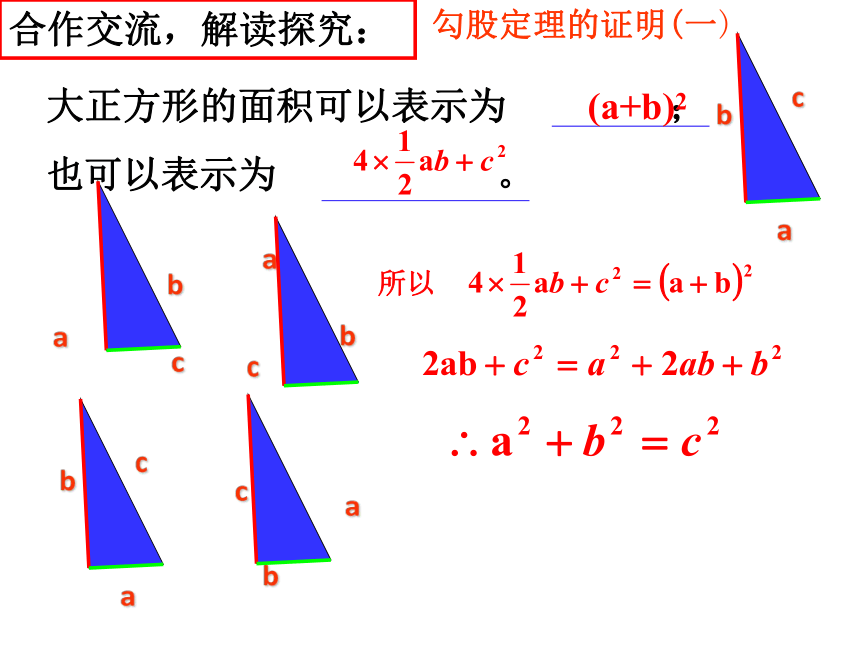
勾股定理的证明(一)
b
a
c
b
a
c
b
a
c
大正方形的面积可以表示为 ;
也可以表示为 。
(a+b)2
所以
b
a
c
合作交流,解读探究:
b
a
c
b
a
c
b
a
c
a
c
b
b
a
c
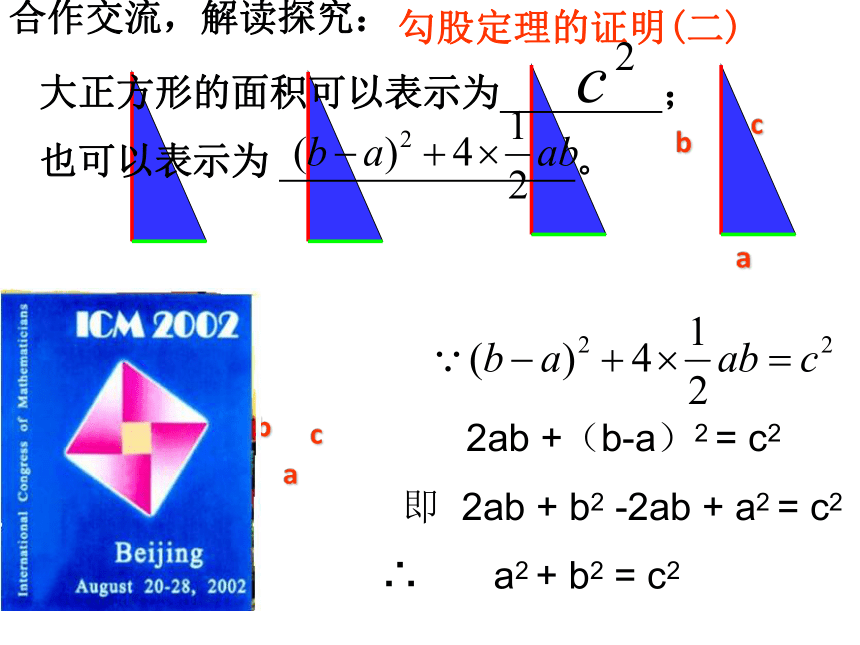
勾股定理的证明(二)
2ab +(b-a)2 = c2
即 2ab + b2 -2ab + a2 = c2
∴ a2 + b2 = c2
合作交流,解读探究:
大正方形的面积可以表示为 ;
也可以表示为 。
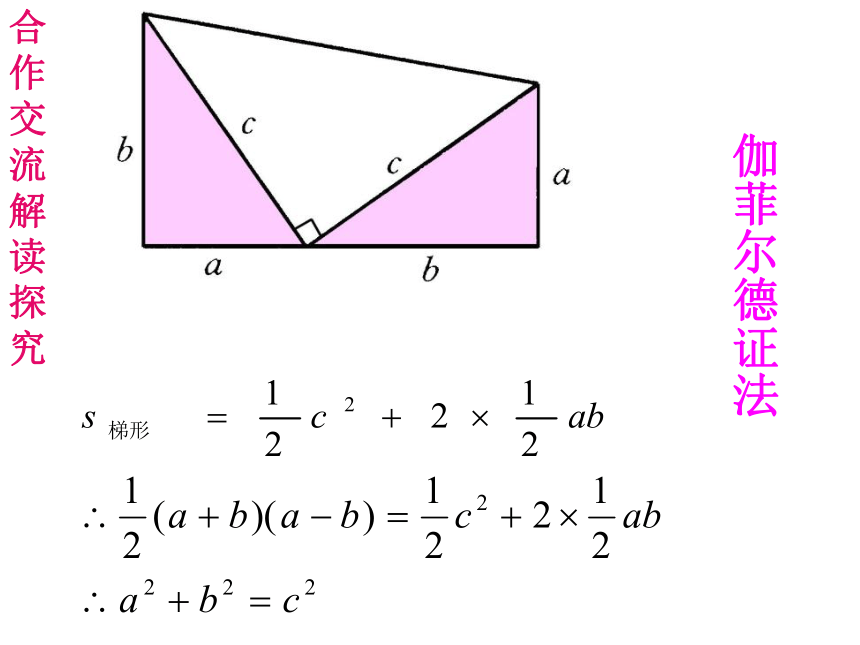
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。
有趣的总统证法
伽菲尔德证法
合作交流解读探究
例1 小丁的妈妈买了一台显示器为22英寸(56厘米)的液晶电脑。小丁量了显示器的屏幕后,发现屏幕只有49厘米长和27厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
荧屏对角线大约为56厘米
解:∵492+272=3130
562=3136
3130
3136
≈
我们通常所说的22英寸或56厘米的电脑显示器或电视机,是指其屏幕对角线的长度
应用迁移,巩固提高
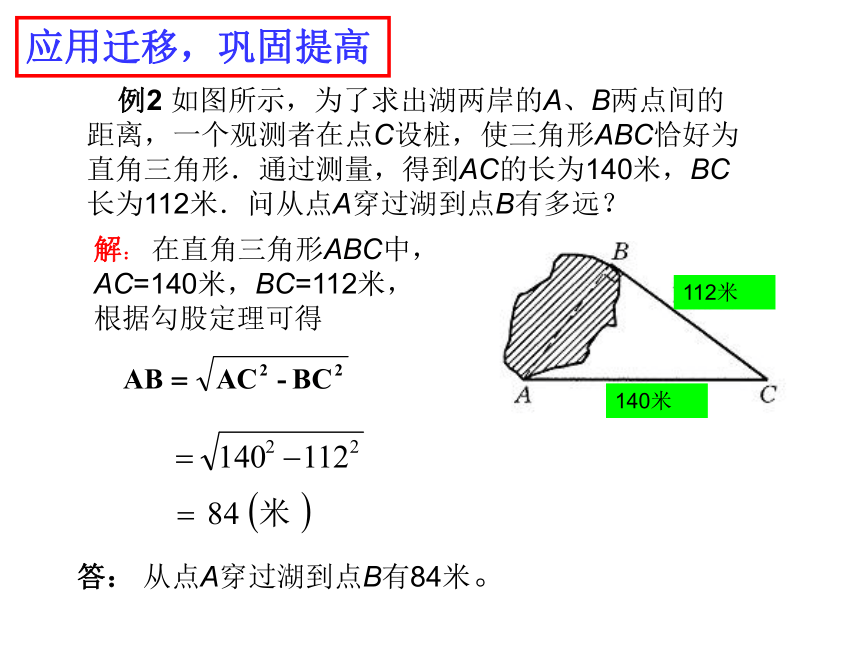
例2 如图所示,为了求出湖两岸的A、B两点间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC的长为140米,BC长为112米.问从点A穿过湖到点B有多远?
答: 从点A穿过湖到点B有84米。
解: 在直角三角形ABC中,
AC=140米,BC=112米,
根据勾股定理可得
应用迁移,巩固提高
140米
112米
B
A
C
D
E
F
G
H
现学现用:
1、如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
2、小明发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米抻直后,发现下端刚好接触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗?
A
B
C
5
x
x+1
现学现用:
1这节课你学到了什么知识?
3、你还有什么疑惑或没有弄懂的地方?
2 运用“勾股定理”应注意什么问题?
小结
4.如图,CD是Rt⊿ABC斜边上的高,若AB= ,AC:BC=4:1,求CD的长。
补充练习
C
A
D
B
3.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D,求CD的长。
(第3、4题)
1.已知等边三角形的边长为2cm,求等边三角形的面积。
2.在⊿ABC中,∠C=90°, AB=12cm,AC=BC,求BC的长。
5.一个等腰三角形的周长为14cm,一边长为4 cm,求底边上的高。
6.一直角三角形的斜边长比一直角边大2,另一直角边长
为6,求斜边长。
8.直角三角形的周长为12cm,斜边长为5cm,求此三角形的面积。
7.等腰三角形腰和底边的比是3:2,若底边为6,求一腰上的高。
作业
1、课本第55页4、5题。
2、阅读课本55页的阅读材料
3、(选做题)《九章算术》勾股章第6题:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长几何?
(本题的意思是:有一水池一丈见方,池中生有一棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长?)
再见!
勾股定理的验证及应用
b
a
c
勾股定理的证明(一)
b
a
c
b
a
c
b
a
c
大正方形的面积可以表示为 ;
也可以表示为 。
(a+b)2
所以
b
a
c
合作交流,解读探究:
b
a
c
b
a
c
b
a
c
a
c
b
b
a
c
勾股定理的证明(二)
2ab +(b-a)2 = c2
即 2ab + b2 -2ab + a2 = c2
∴ a2 + b2 = c2
合作交流,解读探究:
大正方形的面积可以表示为 ;
也可以表示为 。
美国第二十任总统伽菲尔德的证法在数学史上被传为佳话
人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,
就把这一证法称为“总统”证法。
有趣的总统证法
伽菲尔德证法
合作交流解读探究
例1 小丁的妈妈买了一台显示器为22英寸(56厘米)的液晶电脑。小丁量了显示器的屏幕后,发现屏幕只有49厘米长和27厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?
∴售货员没搞错
荧屏对角线大约为56厘米
解:∵492+272=3130
562=3136
3130
3136
≈
我们通常所说的22英寸或56厘米的电脑显示器或电视机,是指其屏幕对角线的长度
应用迁移,巩固提高
例2 如图所示,为了求出湖两岸的A、B两点间的距离,一个观测者在点C设桩,使三角形ABC恰好为直角三角形.通过测量,得到AC的长为140米,BC长为112米.问从点A穿过湖到点B有多远?
答: 从点A穿过湖到点B有84米。
解: 在直角三角形ABC中,
AC=140米,BC=112米,
根据勾股定理可得
应用迁移,巩固提高
140米
112米
B
A
C
D
E
F
G
H
现学现用:
1、如图,小方格都是边长为1的正方形,
求四边形ABCD的面积与周长.
2、小明发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米抻直后,发现下端刚好接触地面,你能帮他们把旗杆的高度和绳子的长度计算出来吗?
A
B
C
5
x
x+1
现学现用:
1这节课你学到了什么知识?
3、你还有什么疑惑或没有弄懂的地方?
2 运用“勾股定理”应注意什么问题?
小结
4.如图,CD是Rt⊿ABC斜边上的高,若AB= ,AC:BC=4:1,求CD的长。
补充练习
C
A
D
B
3.如图,在Rt△ABC中,∠ACB=90°,AB=5cm,BC=3cm,CD⊥AB于D,求CD的长。
(第3、4题)
1.已知等边三角形的边长为2cm,求等边三角形的面积。
2.在⊿ABC中,∠C=90°, AB=12cm,AC=BC,求BC的长。
5.一个等腰三角形的周长为14cm,一边长为4 cm,求底边上的高。
6.一直角三角形的斜边长比一直角边大2,另一直角边长
为6,求斜边长。
8.直角三角形的周长为12cm,斜边长为5cm,求此三角形的面积。
7.等腰三角形腰和底边的比是3:2,若底边为6,求一腰上的高。
作业
1、课本第55页4、5题。
2、阅读课本55页的阅读材料
3、(选做题)《九章算术》勾股章第6题:今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问水深、葭长几何?
(本题的意思是:有一水池一丈见方,池中生有一棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长?)
再见!
