2021-2022学年青岛版数学七年级下册 13.3 圆 课时练习(word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版数学七年级下册 13.3 圆 课时练习(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 61.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览


文档简介
2022年青岛版数学七年级下册
13.3《圆》课时练习
一、选择题
1.有下列四种说法:
①半径确定了,圆就确定了;
②直径是弦;
③弦是直径;
④半圆是弧,但弧不一定是半圆.
其中,错误的说法有( )
A.1种 B.2种 C.3种 D.4种
2.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
A.2 B.3 C.4 D.5
3.下列说法错误的是( )
A.圆上的点到圆心的距离相等
B.过圆心的线段是直径
C.直径是圆中最长的弦
D.半径相等的圆是等圆
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
5.如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.75° B.70° C.65° D.35°
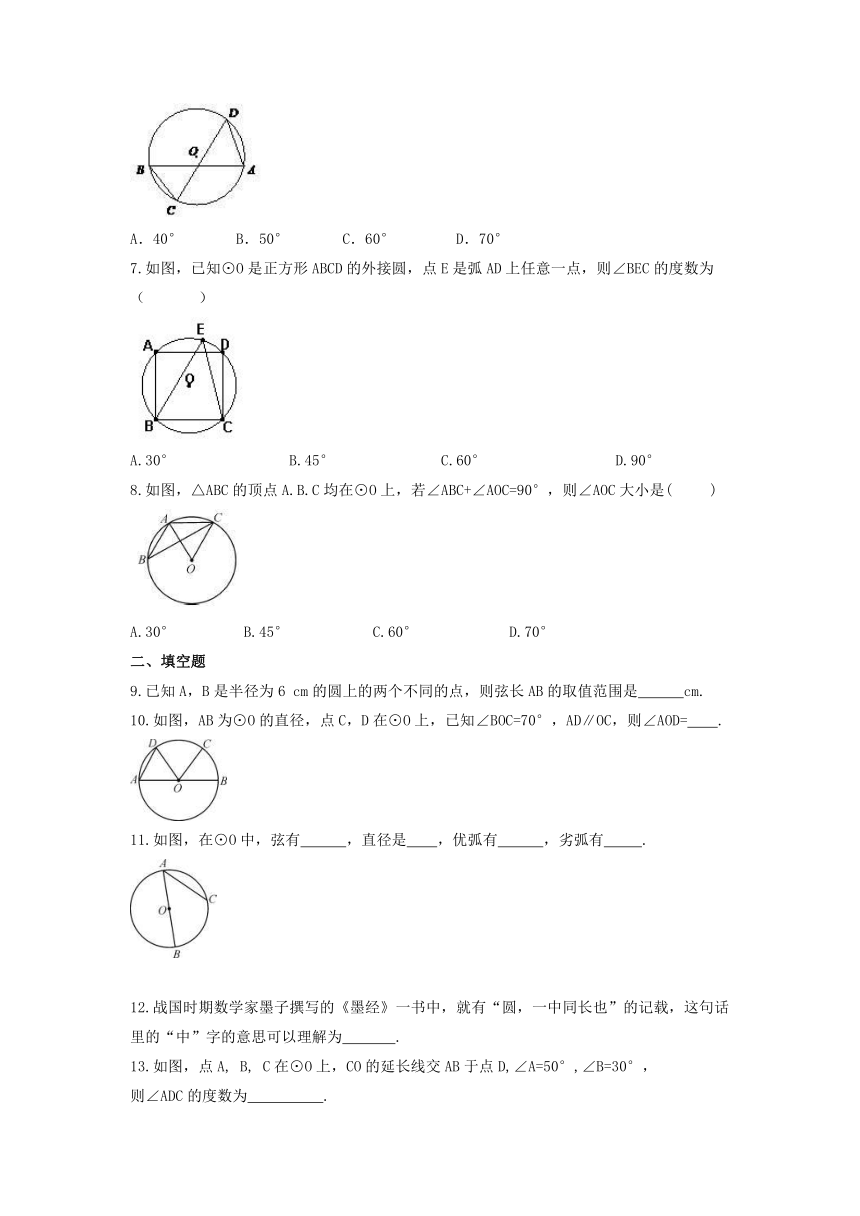
6.如图,AB、CD是⊙O的两条弦,连结AD、BC.若∠BCD=70°,
则∠BAD的度数为( )
A.40° B.50° C.60° D.70°
7.如图,已知⊙O是正方形ABCD的外接圆,点E是弧AD上任意一点,则∠BEC的度数为 ( )
A.30° B.45° C.60° D.90°
8.如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC大小是( )
A.30° B.45° C.60° D.70°
二、填空题
9.已知A,B是半径为6 cm的圆上的两个不同的点,则弦长AB的取值范围是 cm.
10.如图,AB为⊙O的直径,点C,D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD= .
11.如图,在⊙O中,弦有 ,直径是 ,优弧有 ,劣弧有 .
12.战国时期数学家墨子撰写的《墨经》一书中,就有“圆,一中同长也”的记载,这句话里的“中”字的意思可以理解为 .
13.如图,点A, B, C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,
则∠ADC的度数为 .
三、解答题
14.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
15.如图,CE是⊙O的直径,AD的延长线与CE的延长线交于点B,若BD=OD,∠AOC=114°,
求∠AOD的度数.
16.如图,在△ABC中,BD,CE是两条高,点O为BC的中点,连接OD,OE.求证:B,C,D,E四个点在以点O为圆心的同一个圆上.
17.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数.
参考答案
1.答案为:B.
2.答案为:B.
3.答案为:B.
4.答案为:C.
5.答案为:B.
6.答案为:D
7.答案为:B
8.答案为:C
9.答案为:010.答案为:40°.
11.答案为:AC,AB,AB,,,,.
12.答案为:圆心
13.答案为:110°
14.解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
15.解:设∠B=x.
∵BD=OD,
∴∠DOB=∠B=x.
∴∠ADO=∠DOB+∠B=2x.
∵OA=OD,
∴∠A=∠ADO=2x.
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°.
∴∠AOD=180°-∠A-∠ADO=180°-4x=180°-4×38°=28°.
16.证明:∵BD,CE是两条高,
∴∠BDC=∠BEC=90°.
∵点O为BC的中点,
∴OE=OB=OC=BC.
同理:OD=OB=OC=BC.
∴OB=OC=OD=OE.
∴B,C,D,E四个点在以点O为圆心的同一个圆上.
17.解:连结OC,如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
13.3《圆》课时练习
一、选择题
1.有下列四种说法:
①半径确定了,圆就确定了;
②直径是弦;
③弦是直径;
④半圆是弧,但弧不一定是半圆.
其中,错误的说法有( )
A.1种 B.2种 C.3种 D.4种
2.点A、O、D与点B、O、C分别在同一直线上,图中弦的条数为( )
A.2 B.3 C.4 D.5
3.下列说法错误的是( )
A.圆上的点到圆心的距离相等
B.过圆心的线段是直径
C.直径是圆中最长的弦
D.半径相等的圆是等圆
4.如图,在△ABC中,AB为⊙O的直径,∠B=60°,∠BOD=100°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
5.如图,点A,B,C在⊙O上,∠ACB=35°,则∠AOB的度数是( )
A.75° B.70° C.65° D.35°
6.如图,AB、CD是⊙O的两条弦,连结AD、BC.若∠BCD=70°,
则∠BAD的度数为( )
A.40° B.50° C.60° D.70°
7.如图,已知⊙O是正方形ABCD的外接圆,点E是弧AD上任意一点,则∠BEC的度数为 ( )
A.30° B.45° C.60° D.90°
8.如图,△ABC的顶点A.B.C均在⊙O上,若∠ABC+∠AOC=90°,则∠AOC大小是( )
A.30° B.45° C.60° D.70°
二、填空题
9.已知A,B是半径为6 cm的圆上的两个不同的点,则弦长AB的取值范围是 cm.
10.如图,AB为⊙O的直径,点C,D在⊙O上,已知∠BOC=70°,AD∥OC,则∠AOD= .
11.如图,在⊙O中,弦有 ,直径是 ,优弧有 ,劣弧有 .
12.战国时期数学家墨子撰写的《墨经》一书中,就有“圆,一中同长也”的记载,这句话里的“中”字的意思可以理解为 .
13.如图,点A, B, C在⊙O上,CO的延长线交AB于点D,∠A=50°,∠B=30°,
则∠ADC的度数为 .
三、解答题
14.如图所示,AB为⊙O的直径,CD是⊙O的弦,AB、CD的延长线交于点E,已知AB=2DE,∠AEC=20°.求∠AOC的度数.
15.如图,CE是⊙O的直径,AD的延长线与CE的延长线交于点B,若BD=OD,∠AOC=114°,
求∠AOD的度数.
16.如图,在△ABC中,BD,CE是两条高,点O为BC的中点,连接OD,OE.求证:B,C,D,E四个点在以点O为圆心的同一个圆上.
17.如图,AB是半圆O的直径,D是半圆上的一点,∠DOB=75°,DC交BA的延长线于E,交半圆于C,且CE=AO,求∠E的度数.
参考答案
1.答案为:B.
2.答案为:B.
3.答案为:B.
4.答案为:C.
5.答案为:B.
6.答案为:D
7.答案为:B
8.答案为:C
9.答案为:0
11.答案为:AC,AB,AB,,,,.
12.答案为:圆心
13.答案为:110°
14.解:连接OD,如图,
∵AB=2DE,
而AB=2OD,
∴OD=DE,
∴∠DOE=∠E=20°,
∴∠CDO=∠DOE+∠E=40°,
而OC=OD,
∴∠C=∠ODC=40°,
∴∠AOC=∠C+∠E=60°.
15.解:设∠B=x.
∵BD=OD,
∴∠DOB=∠B=x.
∴∠ADO=∠DOB+∠B=2x.
∵OA=OD,
∴∠A=∠ADO=2x.
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°.
∴∠AOD=180°-∠A-∠ADO=180°-4x=180°-4×38°=28°.
16.证明:∵BD,CE是两条高,
∴∠BDC=∠BEC=90°.
∵点O为BC的中点,
∴OE=OB=OC=BC.
同理:OD=OB=OC=BC.
∴OB=OC=OD=OE.
∴B,C,D,E四个点在以点O为圆心的同一个圆上.
17.解:连结OC,如图,
∵CE=AO,
而OA=OC,
∴OC=EC,
∴∠E=∠1,
∴∠2=∠E+∠1=2∠E,
∵OC=OD,
∴∠D=∠2=2∠E,
∵∠BOD=∠E+∠D,
∴∠E+2∠E=75°,
∴∠E=25°.
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
