2021—2022学年人教版八年级数学下册18.1平行四边形课后练习(Word版含答案)
文档属性
| 名称 | 2021—2022学年人教版八年级数学下册18.1平行四边形课后练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 398.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 11:53:53 | ||
图片预览




文档简介
2021——2022学年度人教版八年级数学下册 第十八章 平行四边形 18.1平行四边形课后练习
一、选择题
1.在平面直角坐标系中,以O(0,0)、A(1,1)、B(4,0)为顶点构造平行四边形,下列各点能作为该平行四边形第四个顶点的有( )个.
E(﹣2,1)、F(5,1)、G(1,﹣1)、H(3,﹣1)、I(﹣3,1)
A.2 B.3 C.4 D.5
2.由两个全等三角形用各种不同的方法拼成四边形,在这些拼成的四边形中是平行四边形的个数是( ).A.4个 B.3个 C.2个 D.1个
3.若以A(-0.5,0),B(2,0),C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在平行四边形ABCD中,∠A:∠B:∠C:∠D可以为( )
A.1:2:3:4 B.3:2:3:2 C.2:2:1:1 D.1:3:3:1
5.将△ABC平移得到△,若,则的度数是( )
A.10° B.80° C.100° D.160°
6.如图,在中,,分别是、的中点,点在的延长线上.添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
7.如图,在中,,,,将沿方向向右平移得到.若四边形的面积为,则平移距离是( )
A. B. C. D.
8.如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
A.BE=CE B.AB=BF C.DE=BE D.AB=DC
9.如图,四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( )
A.16 B.20 C.22 D.26
10.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
A.4次 B.3次 C.2次 D.1次
二、填空题
11.如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 ______.
12.如图,在 ABCD中,将△ABC沿着AC所在的直线翻折得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是_____.
13.如图,在中,,分别是和的平分线,,分别与相交于点,,,,则______.
14.在中,AE平分,交CD边于E,,,则的周长为________.
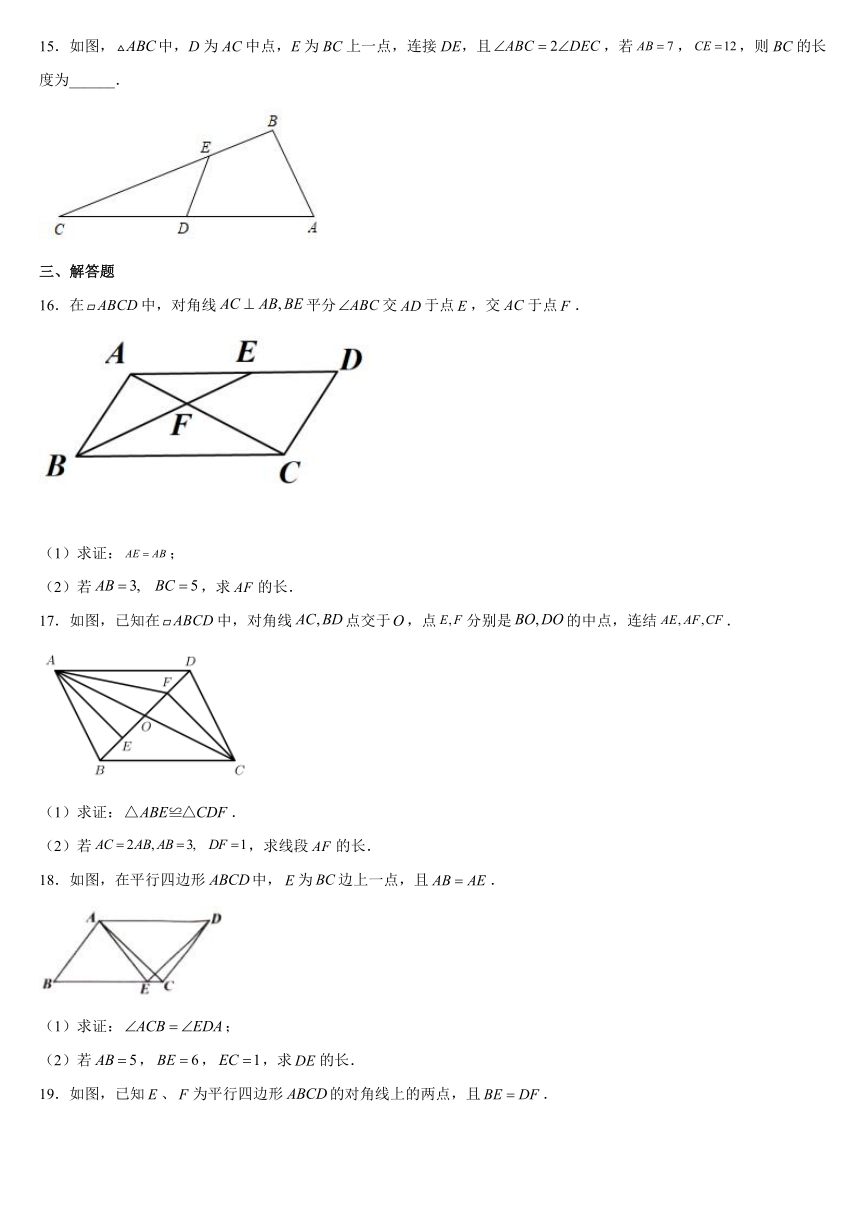
15.如图,中,D为AC中点,E为BC上一点,连接DE,且,若,,则BC的长度为______.
三、解答题
16.在中,对角线平分交于点,交于点.
(1)求证:;
(2)若,求的长.
17.如图,已知在中,对角线点交于,点分别是的中点,连结.
(1)求证:.
(2)若,求线段的长.
18.如图,在平行四边形中,为边上一点,且.
(1)求证:;
(2)若,,,求的长.
19.如图,已知、为平行四边形的对角线上的两点,且.
(1)求证:
(2)若,判断四边形的形状,并说明理由.
20.如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12cm,DE=4cm,求四边形DEFB的周长.
21.如图,在中,,点是所在平面内的一点,过点作交于点,交于点,交于点.
(1)当点在边上时,如图①所示,此时点与点重合,则 .(填“”“”或“”)
(2)当点在内部时,如图②所示,作交于,求证:
①四边形、四边形都是平行四边形;
②.
(3)当点在外部时,如图③所示,、、、这四条线段之间又有着怎样的数量关系?请写出你的猜想,并说明理由.
22.如图1,在等边中,,点D,E分别在边上,,连接,点M,P,N分别为的中点.
(1)观察猜想:图1中,线段与的数量关系是 , ;
(2)探究证明:把绕点A逆时针方向旋转到图2的位置,连接,则上面题(1)中的两个结论是否依然成立,并说明理由;
(3)拓展延伸:把绕点A在平面内自由旋转,若,请直接写出周长的最大值.
23.如图, ABCD的对角线AC、BD相交于点O,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连结PO并延长交BC于点Q.设点P的运动时间为t秒.
(1)求BQ的长,(用含t的代数式表示)
(2)当四边形ABQP是平行四边形时,求t的值
(3)当点O在线段AP的垂直平分线上时,直接写出t的值.
【参考答案】
1.B 2.B 3.C 4.B 5.B 6.C 7.B 8.C 9.C 10.B
11.40°
12.
13.2
14.16
15.17
16.(1)∵四边形ABCD为平行四边形,
∴,
∴
∵平分,
∴,
∴,
∴;
(2)∵,,
∴,
过点F作于点H,
∵平分,,
∴AF=FH,
∵,
∴,
即,
∴.
17.解:(1)∵四边形ABCD是平行四边形,
∴,,,
∴,
∵E、F为OB、OD中点,
∴,
∴在与中,
,
∴≌.
(2)∵四边形ABCD是平行四边形,
∴,
∵,
∴,
又∵E为OB中点,
∴,,
∵,,
∴,,
∴在中,,
∴在中,.
18.(1)证明:∵四边形是平行四边形,
,,
,
,
,
,
在和中
,
,
;
(2)如图,过点作于点,
,,,,
,,
在和中,
由勾股定理得,
,
由(1)得,
.
19.(1)证明∵四边形是平行四边形,
∴,,
∴
在和中,
∴
解:(2)四边形是矩形,理由如下:
∵,
∴,
∴
即
∴
又∵
∴四边形是平行四边形,
∵,
∴平行四边形是矩形.
20.(1)证明:∵点D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE//BC,BC=2DE,
∵CF=3BF,
∴BC=2BF,
∴DE=BF,
∴四边形DEFB是平行四边形;
(2)解:由(1)得:BC=2DE=8(cm),BF=DE=4cm,四边形DEFB是平行四边形,
∴BD=EF,
∵D是AC的中点,AC=12cm,
∴CD=AC=6(cm),
∵∠ACB=90°,
∴BD==10(cm),
∴平行四边形DEFB的周长=2(DE+BD)=2(4+10)=28(cm).
21.解:∵,,
∴,,
∴四边形平行四边形,
∴ ,
∵,
∴ ,
∵,
∴ ,
∴,
∴ ,
∴ ;
(2)证明:①,,
.
,
四边形、四边形都是平行四边形;
②四边形、四边形都是平行四边形,
,,.
,
.
,
,
,
,
;
(3)解:,理由如下:
如图③,作交的延长线于点, 则 ,
,,
四边形、四边形都是平行四边形,
,,
,
,
,
∴ ,
∵ ,
。
∴ ,
∴ ,
∴,
,
∴.
22.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵AD=AE,
∴AB-AD=AC-AE,即BD=CE,
∵M,P,N分别是DE,DC,BC的中点,
∴MP=EC,PM∥EC,PN=BD,PN∥BD,
∴PM=PN,∠MPD=∠ACD,∠NPD=∠ADC,
在△ACD中,∠ADC+∠ACD=180°-∠A=120°,
∴∠MPN=∠MPD+∠NPD=120°.
故答案为:PM=PN,120°;
(2)成立,理由如下:
∵AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ABC=∠ACB=60°,
∴∠BAD=∠CAE,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵DM=ME,DP=PC,BN=NC,
∴MP=EC,PM∥EC,PN=BD,PN∥BD,
∴MP=PN,
∴△PMN是等腰三角形.
∵PM∥CE,
∴∠DPM=∠DCE,
∵PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=60°,
∴∠ACB+∠ABC=120°,
∴∠MPN=120°,
∴PM=PN,∠MPN=120°;
(3)由(2)知:PM=PN,∠MPN=120°,
∵BD≤AB+AD,
∴BD≤14,
∴点D恰好在BA延长线上时,BD、CE取得最大值,且最大值为14,
∴PM 、PN的最大值为7,
此时MN经过点A,即MN垂直平分BC,如图:
∵△ABC、△ADE是等边三角形,且AD=4,AB=10,
∴∠BAN=∠DAM=30°,
∴BN=CN=5,DM=EM=2,
∴AN=5,AM=2,
∴△PMN周长的最大值为PM+PN+MN=7+7+5+2=14+7.
23.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠PAO=∠QCO,
∵∠AOP=∠COQ,
∴△APO≌△CQO(ASA),
∴AP=CQ=t,
∵BC=5,
∴BQ=BC-CQ=5﹣t;
(2)∵AP∥BQ,
当AP=BQ时,四边形ABQP是平行四边形,
即t=5﹣t,
t= ,
∴当t为秒时,四边形ABQP是平行四边形;
(3)t= ,
如图,
在Rt△ABC中,
∵AB=3,BC=5,
∴AC=
∴AO=CO=AC=2,
∴3×4=5×EF,
∴,
∴,
∵OE是AP的垂直平分线,
∴AE=AP=t,∠AEO=90°,
由勾股定理得:AE2+OE2=AO2,
或(舍去)
∴当秒时,点O在线段AP的垂直平分线上.
一、选择题
1.在平面直角坐标系中,以O(0,0)、A(1,1)、B(4,0)为顶点构造平行四边形,下列各点能作为该平行四边形第四个顶点的有( )个.
E(﹣2,1)、F(5,1)、G(1,﹣1)、H(3,﹣1)、I(﹣3,1)
A.2 B.3 C.4 D.5
2.由两个全等三角形用各种不同的方法拼成四边形,在这些拼成的四边形中是平行四边形的个数是( ).A.4个 B.3个 C.2个 D.1个
3.若以A(-0.5,0),B(2,0),C(0,1)三点为顶点要画平行四边形,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在平行四边形ABCD中,∠A:∠B:∠C:∠D可以为( )
A.1:2:3:4 B.3:2:3:2 C.2:2:1:1 D.1:3:3:1
5.将△ABC平移得到△,若,则的度数是( )
A.10° B.80° C.100° D.160°
6.如图,在中,,分别是、的中点,点在的延长线上.添加一个条件使四边形为平行四边形,则这个条件是( )
A. B. C. D.
7.如图,在中,,,,将沿方向向右平移得到.若四边形的面积为,则平移距离是( )
A. B. C. D.
8.如图,平行四边形ABCD中,E是BC边的中点,连接DE并延长交AB的延长线于点F,则在题中条件下,下列结论不能成立的是( )
A.BE=CE B.AB=BF C.DE=BE D.AB=DC
9.如图,四边形ABCD中,点E,F分别在边AD,BC上,线段EF与AC交于点O且互相平分,若AD=BC=10,EF=AB=6,则四边形EFCD的周长是( )
A.16 B.20 C.22 D.26
10.如图,平行四边形ABCD中,AB=8cm,AD=12cm,点P在AD 边上以每秒1cm的速度从点A向点D运动,点Q在BC边上,以每秒4cm的速度从点C出发,在CB间往返运动,两个点同时出发,当点P到达点D时停止(同时点Q也停止),在运动以后,以P、D、Q、B四点组成平行四边形的次数有( )
A.4次 B.3次 C.2次 D.1次
二、填空题
11.如图,在平行四边形ABCD中,E为边CD上的一个点,将△ADE沿AE折叠至△AD′E处,AD′与CE交于点F,若∠B=50°,∠DAE=20°,则∠FED′的大小为 ______.
12.如图,在 ABCD中,将△ABC沿着AC所在的直线翻折得到△AB′C,B′C交AD于点E,连接B′D,若∠B=60°,∠ACB=45°,AC=,则B′D的长是_____.
13.如图,在中,,分别是和的平分线,,分别与相交于点,,,,则______.
14.在中,AE平分,交CD边于E,,,则的周长为________.
15.如图,中,D为AC中点,E为BC上一点,连接DE,且,若,,则BC的长度为______.
三、解答题
16.在中,对角线平分交于点,交于点.
(1)求证:;
(2)若,求的长.
17.如图,已知在中,对角线点交于,点分别是的中点,连结.
(1)求证:.
(2)若,求线段的长.
18.如图,在平行四边形中,为边上一点,且.
(1)求证:;
(2)若,,,求的长.
19.如图,已知、为平行四边形的对角线上的两点,且.
(1)求证:
(2)若,判断四边形的形状,并说明理由.
20.如图,在△ABC中,点D,E分别是AC,AB的中点,点F是CB延长线上的一点,且CF=3BF,连接DB,EF.
(1)求证:四边形DEFB是平行四边形;
(2)若∠ACB=90°,AC=12cm,DE=4cm,求四边形DEFB的周长.
21.如图,在中,,点是所在平面内的一点,过点作交于点,交于点,交于点.
(1)当点在边上时,如图①所示,此时点与点重合,则 .(填“”“”或“”)
(2)当点在内部时,如图②所示,作交于,求证:
①四边形、四边形都是平行四边形;
②.
(3)当点在外部时,如图③所示,、、、这四条线段之间又有着怎样的数量关系?请写出你的猜想,并说明理由.
22.如图1,在等边中,,点D,E分别在边上,,连接,点M,P,N分别为的中点.
(1)观察猜想:图1中,线段与的数量关系是 , ;
(2)探究证明:把绕点A逆时针方向旋转到图2的位置,连接,则上面题(1)中的两个结论是否依然成立,并说明理由;
(3)拓展延伸:把绕点A在平面内自由旋转,若,请直接写出周长的最大值.
23.如图, ABCD的对角线AC、BD相交于点O,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连结PO并延长交BC于点Q.设点P的运动时间为t秒.
(1)求BQ的长,(用含t的代数式表示)
(2)当四边形ABQP是平行四边形时,求t的值
(3)当点O在线段AP的垂直平分线上时,直接写出t的值.
【参考答案】
1.B 2.B 3.C 4.B 5.B 6.C 7.B 8.C 9.C 10.B
11.40°
12.
13.2
14.16
15.17
16.(1)∵四边形ABCD为平行四边形,
∴,
∴
∵平分,
∴,
∴,
∴;
(2)∵,,
∴,
过点F作于点H,
∵平分,,
∴AF=FH,
∵,
∴,
即,
∴.
17.解:(1)∵四边形ABCD是平行四边形,
∴,,,
∴,
∵E、F为OB、OD中点,
∴,
∴在与中,
,
∴≌.
(2)∵四边形ABCD是平行四边形,
∴,
∵,
∴,
又∵E为OB中点,
∴,,
∵,,
∴,,
∴在中,,
∴在中,.
18.(1)证明:∵四边形是平行四边形,
,,
,
,
,
,
在和中
,
,
;
(2)如图,过点作于点,
,,,,
,,
在和中,
由勾股定理得,
,
由(1)得,
.
19.(1)证明∵四边形是平行四边形,
∴,,
∴
在和中,
∴
解:(2)四边形是矩形,理由如下:
∵,
∴,
∴
即
∴
又∵
∴四边形是平行四边形,
∵,
∴平行四边形是矩形.
20.(1)证明:∵点D,E分别是AC,AB的中点,
∴DE是△ABC的中位线,
∴DE//BC,BC=2DE,
∵CF=3BF,
∴BC=2BF,
∴DE=BF,
∴四边形DEFB是平行四边形;
(2)解:由(1)得:BC=2DE=8(cm),BF=DE=4cm,四边形DEFB是平行四边形,
∴BD=EF,
∵D是AC的中点,AC=12cm,
∴CD=AC=6(cm),
∵∠ACB=90°,
∴BD==10(cm),
∴平行四边形DEFB的周长=2(DE+BD)=2(4+10)=28(cm).
21.解:∵,,
∴,,
∴四边形平行四边形,
∴ ,
∵,
∴ ,
∵,
∴ ,
∴,
∴ ,
∴ ;
(2)证明:①,,
.
,
四边形、四边形都是平行四边形;
②四边形、四边形都是平行四边形,
,,.
,
.
,
,
,
,
;
(3)解:,理由如下:
如图③,作交的延长线于点, 则 ,
,,
四边形、四边形都是平行四边形,
,,
,
,
,
∴ ,
∵ ,
。
∴ ,
∴ ,
∴,
,
∴.
22.解:(1)∵△ABC是等边三角形,
∴AB=AC,∠A=60°,
∵AD=AE,
∴AB-AD=AC-AE,即BD=CE,
∵M,P,N分别是DE,DC,BC的中点,
∴MP=EC,PM∥EC,PN=BD,PN∥BD,
∴PM=PN,∠MPD=∠ACD,∠NPD=∠ADC,
在△ACD中,∠ADC+∠ACD=180°-∠A=120°,
∴∠MPN=∠MPD+∠NPD=120°.
故答案为:PM=PN,120°;
(2)成立,理由如下:
∵AB=AC,AD=AE,∠BAC=∠DAE=60°,∠ABC=∠ACB=60°,
∴∠BAD=∠CAE,
∵AB=AC,∠BAD=∠CAE,AD=AE,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∵DM=ME,DP=PC,BN=NC,
∴MP=EC,PM∥EC,PN=BD,PN∥BD,
∴MP=PN,
∴△PMN是等腰三角形.
∵PM∥CE,
∴∠DPM=∠DCE,
∵PN∥BD,
∴∠PNC=∠DBC,
∵∠DPN=∠DCB+∠PNC=∠DCB+∠DBC,
∴∠MPN=∠DPM+∠DPN=∠DCE+∠DCB+∠DBC=∠BCE+∠DBC=∠ACB+∠ACE+∠DBC=∠ACB+∠ABD+∠DBC=∠ACB+∠ABC,
∵∠BAC=60°,
∴∠ACB+∠ABC=120°,
∴∠MPN=120°,
∴PM=PN,∠MPN=120°;
(3)由(2)知:PM=PN,∠MPN=120°,
∵BD≤AB+AD,
∴BD≤14,
∴点D恰好在BA延长线上时,BD、CE取得最大值,且最大值为14,
∴PM 、PN的最大值为7,
此时MN经过点A,即MN垂直平分BC,如图:
∵△ABC、△ADE是等边三角形,且AD=4,AB=10,
∴∠BAN=∠DAM=30°,
∴BN=CN=5,DM=EM=2,
∴AN=5,AM=2,
∴△PMN周长的最大值为PM+PN+MN=7+7+5+2=14+7.
23.解:(1)∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠PAO=∠QCO,
∵∠AOP=∠COQ,
∴△APO≌△CQO(ASA),
∴AP=CQ=t,
∵BC=5,
∴BQ=BC-CQ=5﹣t;
(2)∵AP∥BQ,
当AP=BQ时,四边形ABQP是平行四边形,
即t=5﹣t,
t= ,
∴当t为秒时,四边形ABQP是平行四边形;
(3)t= ,
如图,
在Rt△ABC中,
∵AB=3,BC=5,
∴AC=
∴AO=CO=AC=2,
∴3×4=5×EF,
∴,
∴,
∵OE是AP的垂直平分线,
∴AE=AP=t,∠AEO=90°,
由勾股定理得:AE2+OE2=AO2,
或(舍去)
∴当秒时,点O在线段AP的垂直平分线上.
