柱锥台的结构特征
图片预览








文档简介
课件30张PPT。章丘七中高一数学组 书 山 有 路 勤 为 径,学 海 无 崖 苦 作 舟少 小 不 学 习,老 来 徒 伤 悲 成功=艰苦的劳动+正确的方法+少谈空话天才就是百分之一的灵感,百分之九十九的汗水!天 才 在 于 勤 奋,努 力 才 能 成 功! 棱柱、棱锥和棱台
的结构特征勤劳的孩子展望未来, 但懒惰的孩子享受现在!!!什 么 也 不 问 的 人 什 么 也 学 不 到 !!!怀 天 下 , 求 真 知 , 学 做 人同学们!准备好了吗?★课本,导学案,双色笔
★最重要的是激情!!!榜样就在身边孙玉凤、张燕、 王松、
朱彪、 李鸿豆、李梦梦、
张继峰、赵旗、 张德玉优秀个人卷面整洁、完成率高、答对率高学习目标 1、认识棱柱、棱锥、棱台的结构特征;
2、理解棱柱、棱锥、棱台的特征性质
并会进行简单应用
3、在自主学习、合作探究过程中提升自身能力
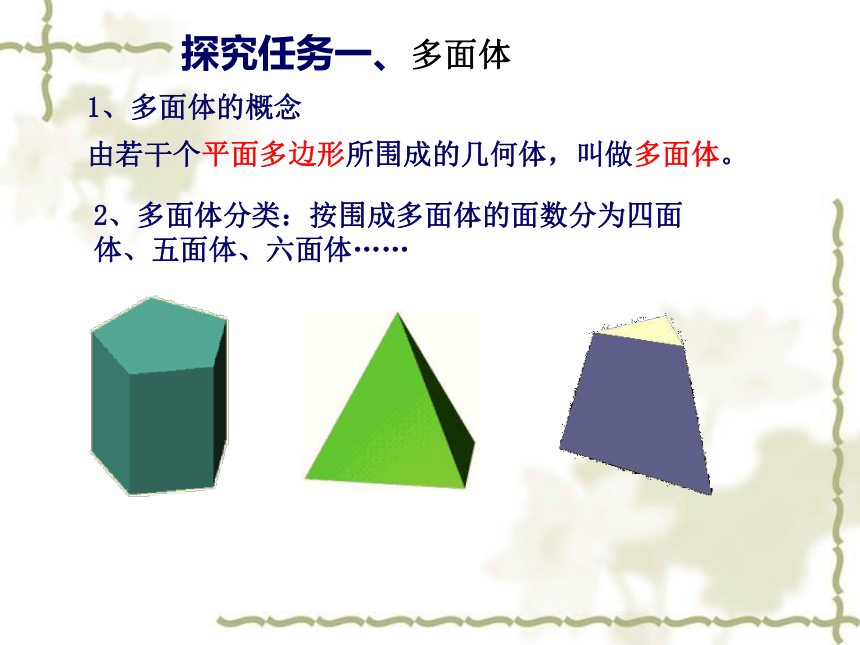
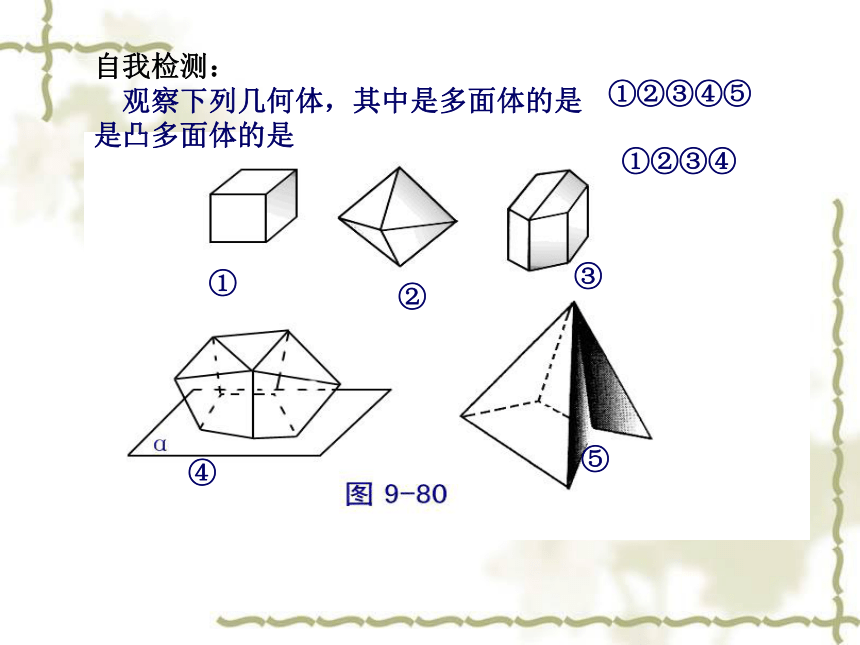
4、激情投入,勇于展示,享受学习的快乐。根据形状,图片中的物体分为哪几类几何体?一、问题引入 上面提到的物体的形状有以下三类:棱柱棱锥棱台探究任务一、多面体 1、多面体的概念由若干个平面多边形所围成的几何体,叫做多面体。2、多面体分类:按围成多面体的面数分为四面体、五面体、六面体……自我检测:
观察下列几何体,其中是多面体的是
是凸多面体的是
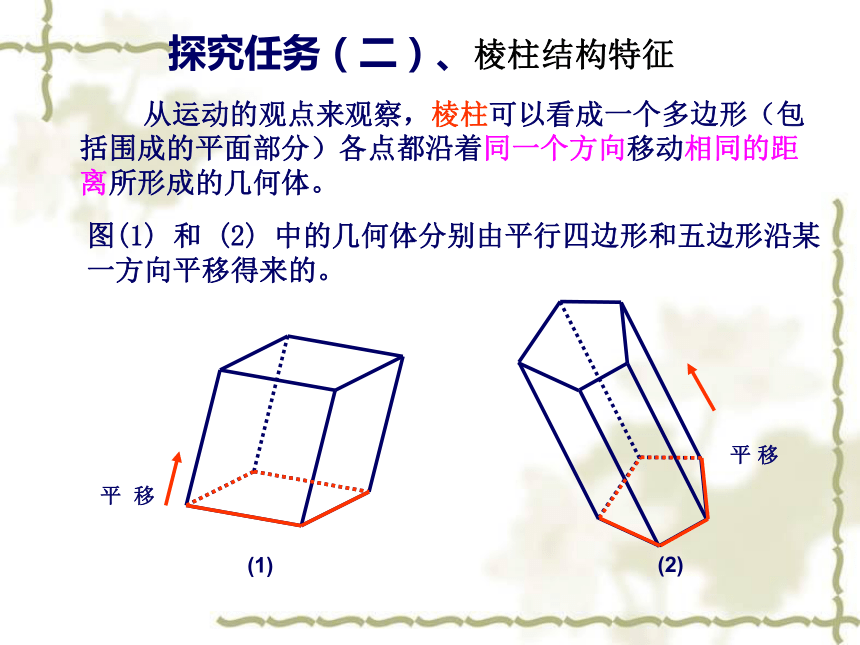
①②③④⑤①②③④ 从运动的观点来观察,棱柱可以看成一个多边形(包括围成的平面部分)各点都沿着同一个方向移动相同的距离所形成的几何体。图(1) 和 (2) 中的几何体分别由平行四边形和五边形沿某一方向平移得来的。(1)(2)探究任务(二)、棱柱结构特征 完成模型制作---将平面图形折成
几何体
制作完成后请展示并指明几何体的形状
通过观察,你发现棱柱具有哪些特征?想一想?1、有两个互相平行的面
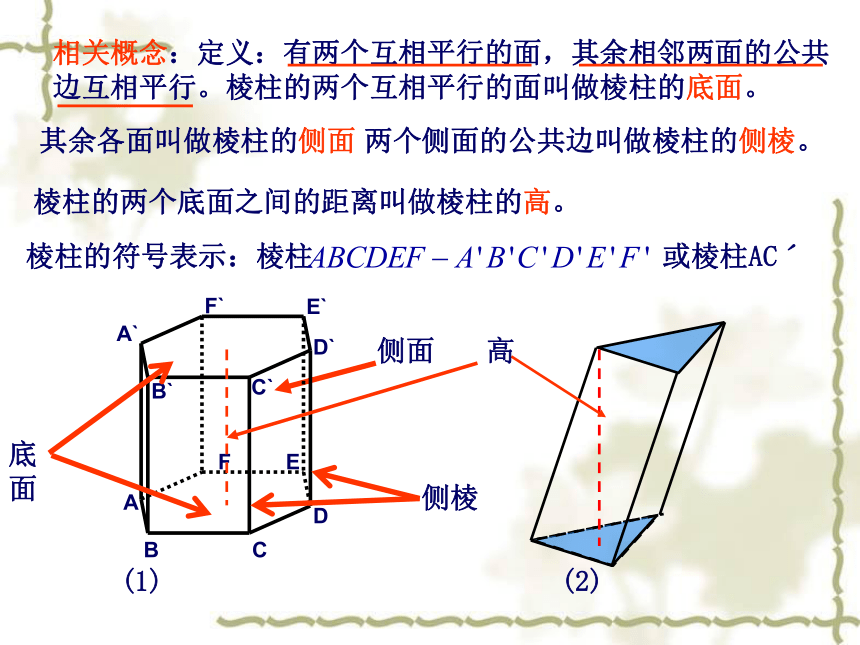
2、夹在两个平行平面间的相邻两个 面的公共边互相平行相关概念:定义:有两个互相平行的面,其余相邻两面的公共边互相平行。棱柱的两个互相平行的面叫做棱柱的底面。 棱柱的两个底面之间的距离叫做棱柱的高。棱柱的符号表示:棱柱 两个侧面的公共边叫做棱柱的侧棱。(1)(2)高或棱柱ACˊ其余各面叫做棱柱的侧面自我检测 : 1、过BC的截面截去长方体的一角,截去的几何体是不是棱柱?余下的几何体是不是棱柱?是棱柱时如何表示? 2、观察右边的六棱柱ABCDEF-A1B1C1D1E1F1,共有多少对平行平面?能作为棱柱的底面的有几对?是4对1对是棱柱ABEˊAˊ-DCFˊDˊ棱柱BBˊEˊ-CCˊFˊABCDEFA1B1C1D1F1E1棱柱的分类按底面多边形边数分为三棱柱、四棱柱、五棱柱,……A1C1B1F`E`D`C`B`A`E1F1D1按侧棱与底面是否垂直分为斜棱柱、直棱柱。斜三棱柱直四棱柱直五棱柱正六棱柱底面是正多边形的直棱柱叫做正棱柱。1234特殊的四棱柱底面是平行四边形的棱柱叫做平行六面体侧棱与底面垂直的平行六面体叫做直平行六面体平行六面体底面是矩形的直平行六面体是长方体直平行六面体长方体正方体棱长都相等的长方体是正方体。小组内讨论棱柱自我检测,
讨论结束,组内派代表上台展示。个人展示要求1、展示时,表达清楚,声音洪亮。2、为他人点评补充时 ,言简意赅。 从运动的观点来观察,棱锥可以看成是当棱柱的一个底面收缩为一个点时,得到的几何体。棱柱与棱锥请同学们仔细观察下面的棱锥,它们有哪些共同的特点?探究任务三、棱锥、棱台的结构特征 通过观察,你发现棱锥具有哪些特点?想一想?1、有一个面是多边形
2、其余的面都是有一个公共顶点的三角形。概念:棱锥是有一个面是多边形,其余各面是有一个公共顶点的三角形的多面体。棱锥中有公共顶点的各三角形叫做棱锥的侧面;各侧面的公共定点叫做棱锥的顶点;相邻两个侧面的公共边叫做棱锥的侧棱;多边形叫做棱锥的底面;顶点到底面的距离叫做棱锥的高。棱锥的符号表示:棱锥侧棱或S-AC棱锥的分类按底面多边形边数分为三棱锥、四棱锥、五棱锥,……三棱锥四棱锥五棱锥正六棱锥如果底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这样的棱锥叫做正棱锥。(1)(2)(3)(4)正棱锥的性质:正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,这些等腰三角形底边上的高也叫棱锥的斜高。SABCDE斜高学生活动:设计一个平面图形,使它能够折成一个
侧面与底面都是等边三角形的正三棱锥 。 答案:作一个等边三角形及其三条中位线,以中位线为折痕即可折成符合题意的几何体2、为他人点评补充时 ,言简意赅。棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分. 棱台及其相关概念棱锥棱台概念:原棱锥的底面和截面分别叫做棱台的下底面、上底面;其它各面叫做棱台的侧面;相邻两个侧面的公共边叫做棱台的侧棱;两个底面之间的距离叫做棱台的高。棱台的符号表示:棱台由正棱锥截得的棱台叫做正棱台;正棱台各侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高斜高高或棱台ACˊ自我检测 :1、底面是正多边形的棱锥一定是正棱锥吗?不一定是2、延长一个棱台的各条侧棱,它们是否相交于一点?是你学到了什么?课堂小结你领会到了哪些应该注意的问题?1、你知道棱柱、棱锥、棱台的特征性质了吗?2、你会用它们的性质解决具体问题了吗?三、应用举例例.已知正四棱锥V-ABCD,底面面积为16,一条侧棱长为 ,计算它的高和斜高。AVBCD解:设VO为正四棱锥V-ABCD的高,作OM⊥BC于点M,则M为BC中点。连接VM,OB,则VO⊥OM,VO⊥OB.
∵S正方形ABCD=16∴BC=4,BM=OM=2,作业:请完成学案的课后检测。 谢 谢 !
再 见!
的结构特征勤劳的孩子展望未来, 但懒惰的孩子享受现在!!!什 么 也 不 问 的 人 什 么 也 学 不 到 !!!怀 天 下 , 求 真 知 , 学 做 人同学们!准备好了吗?★课本,导学案,双色笔
★最重要的是激情!!!榜样就在身边孙玉凤、张燕、 王松、
朱彪、 李鸿豆、李梦梦、
张继峰、赵旗、 张德玉优秀个人卷面整洁、完成率高、答对率高学习目标 1、认识棱柱、棱锥、棱台的结构特征;
2、理解棱柱、棱锥、棱台的特征性质
并会进行简单应用
3、在自主学习、合作探究过程中提升自身能力
4、激情投入,勇于展示,享受学习的快乐。根据形状,图片中的物体分为哪几类几何体?一、问题引入 上面提到的物体的形状有以下三类:棱柱棱锥棱台探究任务一、多面体 1、多面体的概念由若干个平面多边形所围成的几何体,叫做多面体。2、多面体分类:按围成多面体的面数分为四面体、五面体、六面体……自我检测:
观察下列几何体,其中是多面体的是
是凸多面体的是
①②③④⑤①②③④ 从运动的观点来观察,棱柱可以看成一个多边形(包括围成的平面部分)各点都沿着同一个方向移动相同的距离所形成的几何体。图(1) 和 (2) 中的几何体分别由平行四边形和五边形沿某一方向平移得来的。(1)(2)探究任务(二)、棱柱结构特征 完成模型制作---将平面图形折成
几何体
制作完成后请展示并指明几何体的形状
通过观察,你发现棱柱具有哪些特征?想一想?1、有两个互相平行的面
2、夹在两个平行平面间的相邻两个 面的公共边互相平行相关概念:定义:有两个互相平行的面,其余相邻两面的公共边互相平行。棱柱的两个互相平行的面叫做棱柱的底面。 棱柱的两个底面之间的距离叫做棱柱的高。棱柱的符号表示:棱柱 两个侧面的公共边叫做棱柱的侧棱。(1)(2)高或棱柱ACˊ其余各面叫做棱柱的侧面自我检测 : 1、过BC的截面截去长方体的一角,截去的几何体是不是棱柱?余下的几何体是不是棱柱?是棱柱时如何表示? 2、观察右边的六棱柱ABCDEF-A1B1C1D1E1F1,共有多少对平行平面?能作为棱柱的底面的有几对?是4对1对是棱柱ABEˊAˊ-DCFˊDˊ棱柱BBˊEˊ-CCˊFˊABCDEFA1B1C1D1F1E1棱柱的分类按底面多边形边数分为三棱柱、四棱柱、五棱柱,……A1C1B1F`E`D`C`B`A`E1F1D1按侧棱与底面是否垂直分为斜棱柱、直棱柱。斜三棱柱直四棱柱直五棱柱正六棱柱底面是正多边形的直棱柱叫做正棱柱。1234特殊的四棱柱底面是平行四边形的棱柱叫做平行六面体侧棱与底面垂直的平行六面体叫做直平行六面体平行六面体底面是矩形的直平行六面体是长方体直平行六面体长方体正方体棱长都相等的长方体是正方体。小组内讨论棱柱自我检测,
讨论结束,组内派代表上台展示。个人展示要求1、展示时,表达清楚,声音洪亮。2、为他人点评补充时 ,言简意赅。 从运动的观点来观察,棱锥可以看成是当棱柱的一个底面收缩为一个点时,得到的几何体。棱柱与棱锥请同学们仔细观察下面的棱锥,它们有哪些共同的特点?探究任务三、棱锥、棱台的结构特征 通过观察,你发现棱锥具有哪些特点?想一想?1、有一个面是多边形
2、其余的面都是有一个公共顶点的三角形。概念:棱锥是有一个面是多边形,其余各面是有一个公共顶点的三角形的多面体。棱锥中有公共顶点的各三角形叫做棱锥的侧面;各侧面的公共定点叫做棱锥的顶点;相邻两个侧面的公共边叫做棱锥的侧棱;多边形叫做棱锥的底面;顶点到底面的距离叫做棱锥的高。棱锥的符号表示:棱锥侧棱或S-AC棱锥的分类按底面多边形边数分为三棱锥、四棱锥、五棱锥,……三棱锥四棱锥五棱锥正六棱锥如果底面是正多边形,且它的顶点在过底面中心且与底面垂直的直线上,这样的棱锥叫做正棱锥。(1)(2)(3)(4)正棱锥的性质:正棱锥各侧面都是全等的等腰三角形,这些等腰三角形底边上的高都相等,这些等腰三角形底边上的高也叫棱锥的斜高。SABCDE斜高学生活动:设计一个平面图形,使它能够折成一个
侧面与底面都是等边三角形的正三棱锥 。 答案:作一个等边三角形及其三条中位线,以中位线为折痕即可折成符合题意的几何体2、为他人点评补充时 ,言简意赅。棱台是棱锥被平行于底面的一个平面所截后,截面和底面之间的部分. 棱台及其相关概念棱锥棱台概念:原棱锥的底面和截面分别叫做棱台的下底面、上底面;其它各面叫做棱台的侧面;相邻两个侧面的公共边叫做棱台的侧棱;两个底面之间的距离叫做棱台的高。棱台的符号表示:棱台由正棱锥截得的棱台叫做正棱台;正棱台各侧面都是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高斜高高或棱台ACˊ自我检测 :1、底面是正多边形的棱锥一定是正棱锥吗?不一定是2、延长一个棱台的各条侧棱,它们是否相交于一点?是你学到了什么?课堂小结你领会到了哪些应该注意的问题?1、你知道棱柱、棱锥、棱台的特征性质了吗?2、你会用它们的性质解决具体问题了吗?三、应用举例例.已知正四棱锥V-ABCD,底面面积为16,一条侧棱长为 ,计算它的高和斜高。AVBCD解:设VO为正四棱锥V-ABCD的高,作OM⊥BC于点M,则M为BC中点。连接VM,OB,则VO⊥OM,VO⊥OB.
∵S正方形ABCD=16∴BC=4,BM=OM=2,作业:请完成学案的课后检测。 谢 谢 !
再 见!
