2021—2022学年人教版数学八年级下册17.1.1勾股定理复习课课件(共20张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册17.1.1勾股定理复习课课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 328.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览



文档简介
(共20张PPT)
勾股定理复习
知识链接
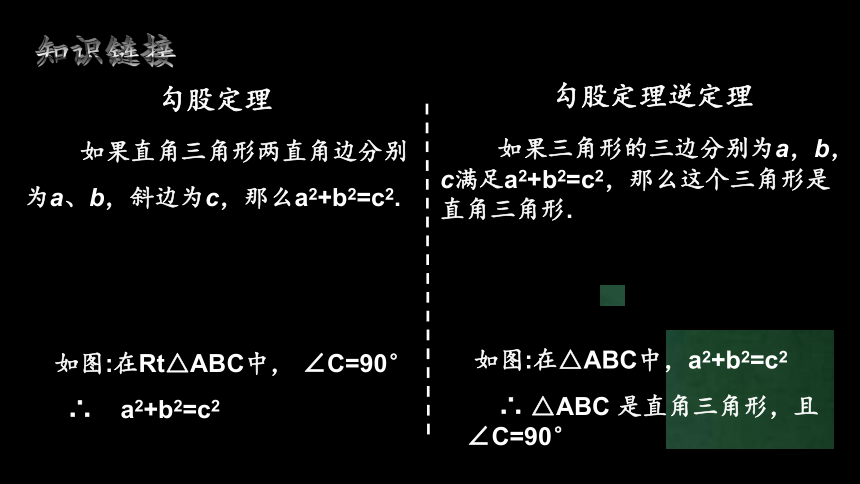
勾股定理
如果直角三角形两直角边分别
为a、b,斜边为c,那么a2+b2=c2.
如图:在Rt△ABC中, ∠C=90°
∴ a2+b2=c2
a
b
c
A
B
C
勾股定理逆定理
如果三角形的三边分别为a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
如图:在△ABC中,a2+b2=c2
∴ △ABC 是直角三角形,且∠C=90°
.
a
b
c
A
B
C
问题探究1
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG,求BG的长.
分析:
3
3
折
叠
①AD=AF
②∠AFE=∠D=90°
③EF=DE=3
AB=AF
∠AFG=90°
AG为公共边
Rt△ABG≌Rt△AFG
BG=GF
3
x
x
6-x
(6-x)2 + 32 =(3+x)2
问题探究1
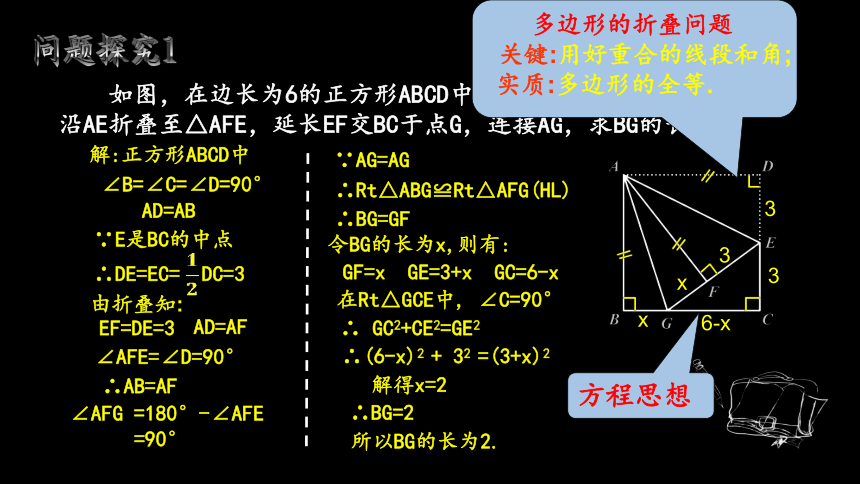
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG,求BG的长.
3
3
3
x
x
6-x
解:正方形ABCD中
∠AFG =180°-∠AFE
=90°
AD=AB
由折叠知:
∵E是BC的中点
∴DE=EC= DC=3
AD=AF
∠AFE=∠D=90°
EF=DE=3
∴AB=AF
∠B=∠C=∠D=90°
∵AG=AG
∴Rt△ABG≌Rt△AFG(HL)
∴BG=GF
令BG的长为x,则有:
GF=x GE=3+x GC=6-x
在Rt△GCE中, ∠C=90°
∴ GC2+CE2=GE2
∴(6-x)2 + 32 =(3+x)2
解得x=2
∴BG=2
所以BG的长为2.
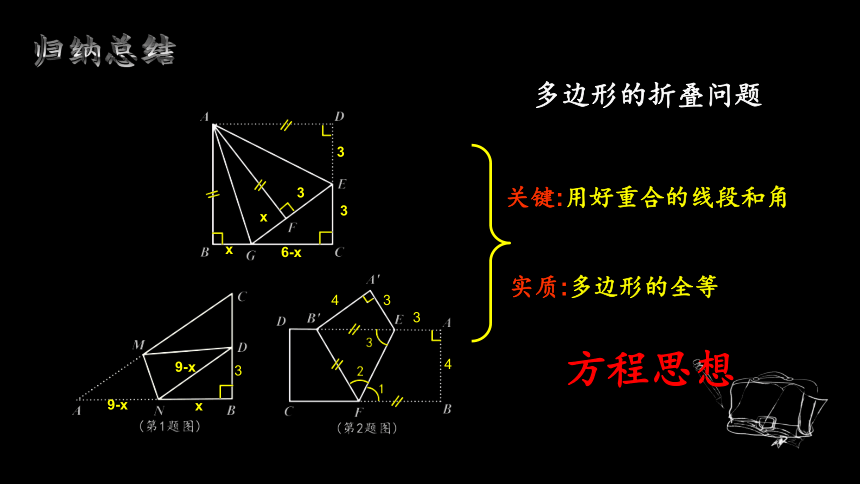
多边形的折叠问题
关键:用好重合的线段和角;
实质:多边形的全等.
方程思想
及时练习
1.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,求BN的长.
2.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,求BF的长.
及时练习
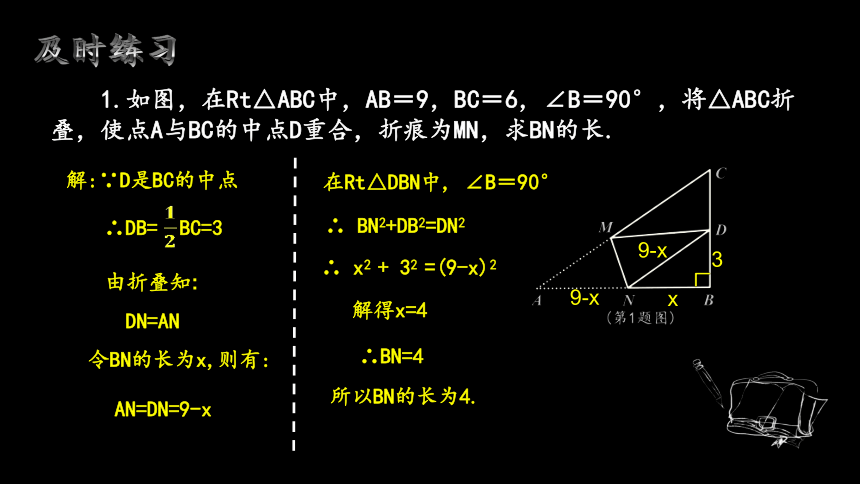
1.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,求BN的长.
3
9-x
x
9-x
解:∵D是BC的中点
∴DB= BC=3
由折叠知:
DN=AN
令BN的长为x,则有:
AN=DN=9-x
在Rt△DBN中, ∠B=90°
∴ BN2+DB2=DN2
∴ x2 + 32 =(9-x)2
解得x=4
∴BN=4
所以BN的长为4.
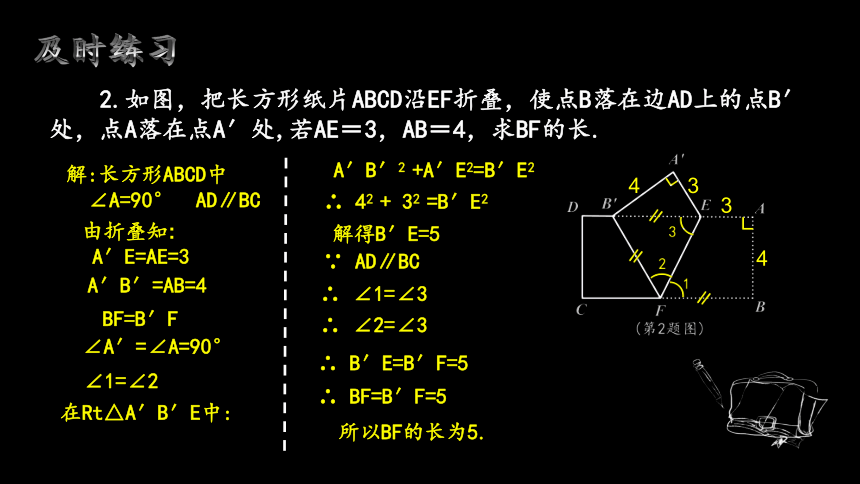
2.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,求BF的长.
及时练习
3
3
4
4
∠A′=∠A=90°
A′E=AE=3
解:长方形ABCD中
∠A=90° AD∥BC
A′B′=AB=4
由折叠知:
BF=B′F
∠1=∠2
在Rt△A′B′E中:
A′B′2 +A′E2=B′E2
∴ 42 + 32 =B′E2
解得B′E=5
∵ AD∥BC
∴ ∠1=∠3
∴ ∠2=∠3
∴ B′E=B′F=5
∴ BF=B′F=5
所以BF的长为5.
归纳总结
方程思想
实质:多边形的全等
关键:用好重合的线段和角
3
3
3
x
x
6-x
3
9-x
x
9-x
3
3
4
4
多边形的折叠问题
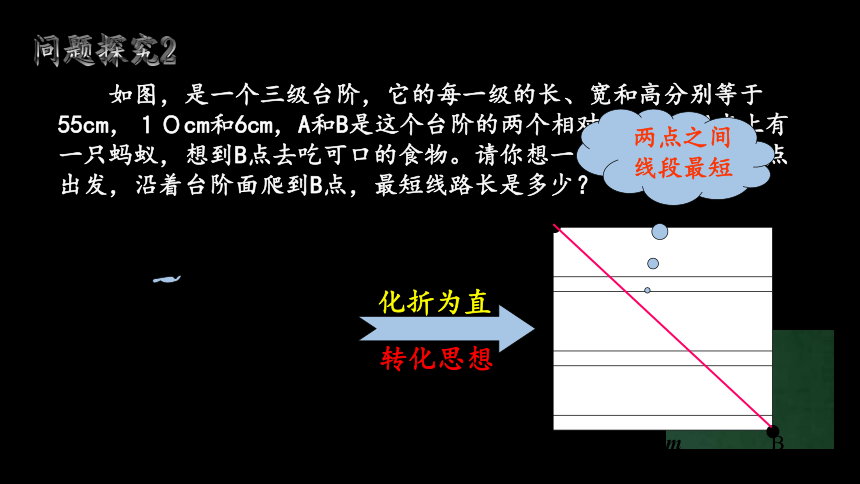
问题探究2
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路长是多少?
A
B
C
55cm
48cm
B
A
55cm
6cm
10cm
化折为直
转化思想
两点之间
线段最短
问题探究2
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路长是多少?
A
B
C
55cm
48cm
解:画出台阶的平面展开图,由题意得:
∠ACB=90°,BC=55cm,AC=48cm
AB的长为所求.
在Rt△ACB中:AC2+BC2=AB2
∴ 482 + 552 =AB2
解得AB=73(cm)
所以蚂蚁爬行的最短线路长73cm.
及时练习
如图,有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
B
A
C
D
E
CE=24m CD=6m
12
1
5
解:画出圆柱体的平面展开图,由题意得:
∠ACB=90°,CE=24m,AD=1m,点B为CE的中点,AB的长为所求.
∴ AC=CD-AD=5
∵点B为CE的中点
∴CB= CE=12
在Rt△ACB中:AC2+BC2=AB2
∴ 52 + 122 =AB2
解得AB=13(m)
所以老鼠爬行的最短线路长13m.
化曲为直
转化思想
两点之间
线段最短
A
B
D
C
归纳总结
A
B
B
A
C
D
E
12
1
5
化曲为直
A
B
C
55cm
48cm
B
A
55cm
6cm
10cm
化折为直
A
B
B
A
C
D
E
12
1
5
化曲为直
几何体的最短路径问题
转化思想
实质:两点之间线段最短
关键:实际问题转化数学问题
拓展延伸
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小虫爬行的最短路线长。
使PA+PG的值最小
“将军饮马”问题
转 化
拓展延伸
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小动物爬行的最短路线长。
使PA+PG的值最小
此时:PA+PG=PA′+PG
=A′G
60
20
60
拓展延伸
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小虫爬行的最短路线长。
60
20
60
解:如图,作点A关于BC的对称点A′,连接A′G交BC于点P,连接PA、PG,小虫沿着A→P→G的路线爬行时路线长最短,即此时PA+PG的值最小.
由题意知:
AE=40cm EG=60cm
∠A′EG=90°
在Rt△ A ′EG中:
A′E2+EG2 = A′G2
∴ 802 + 602 = A′G2
解得A′G=100
即小虫爬行的最短线路长100cm.
由作图知:A′B=AB=60cm
PA′=PA
∴ BE=AB-AE=20
∴ A′E= A′B+BE=80
∴ PA+PG=PA ′+PG=A′G
=100(cm)
课堂小结
勾
股
定
理
多边形的
折叠问题
几何体的
最短路径
+
+
实质:多边形的全等
关键:用好重合的线段和角
实质:两点之间线段最短
关键:实际问题转化数学问题
方程
思想
转化
思想
课后作业
1、如图所示,有一块直角三角形纸片,∠C=90 ,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则BD的长为________.
2、如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上。若AD=3,DE=1,则AB=_________.
(第1题图)
(第2题图)
课后作业
3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是________.
4、葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎藤常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,如图,它的底面周长是50cm,当一段葛藤绕树干均匀盘旋2圈升高为2.4m时,这段葛藤的长是_________.
A
B
(第3题图)
(第4题图)
课后作业
1、如图所示,有一块直角三角形纸片,∠C=90 ,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则BD的长为________.
2、如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上。若AD=3,DE=1,则AB=_________.
(第1题图)
(第2题图)
课后作业
3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是________.
4、葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎藤常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,如图,它的底面周长是50cm,当一段葛藤绕树干均匀盘旋2圈升高为2.4m时,这段葛藤的长是_________.
A
B
(第3题图)
(第4题图)
勾股定理复习
知识链接
勾股定理
如果直角三角形两直角边分别
为a、b,斜边为c,那么a2+b2=c2.
如图:在Rt△ABC中, ∠C=90°
∴ a2+b2=c2
a
b
c
A
B
C
勾股定理逆定理
如果三角形的三边分别为a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
如图:在△ABC中,a2+b2=c2
∴ △ABC 是直角三角形,且∠C=90°
.
a
b
c
A
B
C
问题探究1
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG,求BG的长.
分析:
3
3
折
叠
①AD=AF
②∠AFE=∠D=90°
③EF=DE=3
AB=AF
∠AFG=90°
AG为公共边
Rt△ABG≌Rt△AFG
BG=GF
3
x
x
6-x
(6-x)2 + 32 =(3+x)2
问题探究1
如图,在边长为6的正方形ABCD中,E是边CD的中点,将△ADE沿AE折叠至△AFE,延长EF交BC于点G,连接AG,求BG的长.
3
3
3
x
x
6-x
解:正方形ABCD中
∠AFG =180°-∠AFE
=90°
AD=AB
由折叠知:
∵E是BC的中点
∴DE=EC= DC=3
AD=AF
∠AFE=∠D=90°
EF=DE=3
∴AB=AF
∠B=∠C=∠D=90°
∵AG=AG
∴Rt△ABG≌Rt△AFG(HL)
∴BG=GF
令BG的长为x,则有:
GF=x GE=3+x GC=6-x
在Rt△GCE中, ∠C=90°
∴ GC2+CE2=GE2
∴(6-x)2 + 32 =(3+x)2
解得x=2
∴BG=2
所以BG的长为2.
多边形的折叠问题
关键:用好重合的线段和角;
实质:多边形的全等.
方程思想
及时练习
1.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,求BN的长.
2.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,求BF的长.
及时练习
1.如图,在Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使点A与BC的中点D重合,折痕为MN,求BN的长.
3
9-x
x
9-x
解:∵D是BC的中点
∴DB= BC=3
由折叠知:
DN=AN
令BN的长为x,则有:
AN=DN=9-x
在Rt△DBN中, ∠B=90°
∴ BN2+DB2=DN2
∴ x2 + 32 =(9-x)2
解得x=4
∴BN=4
所以BN的长为4.
2.如图,把长方形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处,若AE=3,AB=4,求BF的长.
及时练习
3
3
4
4
∠A′=∠A=90°
A′E=AE=3
解:长方形ABCD中
∠A=90° AD∥BC
A′B′=AB=4
由折叠知:
BF=B′F
∠1=∠2
在Rt△A′B′E中:
A′B′2 +A′E2=B′E2
∴ 42 + 32 =B′E2
解得B′E=5
∵ AD∥BC
∴ ∠1=∠3
∴ ∠2=∠3
∴ B′E=B′F=5
∴ BF=B′F=5
所以BF的长为5.
归纳总结
方程思想
实质:多边形的全等
关键:用好重合的线段和角
3
3
3
x
x
6-x
3
9-x
x
9-x
3
3
4
4
多边形的折叠问题
问题探究2
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路长是多少?
A
B
C
55cm
48cm
B
A
55cm
6cm
10cm
化折为直
转化思想
两点之间
线段最短
问题探究2
如图,是一个三级台阶,它的每一级的长、宽和高分别等于55cm,10cm和6cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物。请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路长是多少?
A
B
C
55cm
48cm
解:画出台阶的平面展开图,由题意得:
∠ACB=90°,BC=55cm,AC=48cm
AB的长为所求.
在Rt△ACB中:AC2+BC2=AB2
∴ 482 + 552 =AB2
解得AB=73(cm)
所以蚂蚁爬行的最短线路长73cm.
及时练习
如图,有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m的A处爬行到对角B处吃食物,它爬行的最短路线长为多少?
B
A
C
D
E
CE=24m CD=6m
12
1
5
解:画出圆柱体的平面展开图,由题意得:
∠ACB=90°,CE=24m,AD=1m,点B为CE的中点,AB的长为所求.
∴ AC=CD-AD=5
∵点B为CE的中点
∴CB= CE=12
在Rt△ACB中:AC2+BC2=AB2
∴ 52 + 122 =AB2
解得AB=13(m)
所以老鼠爬行的最短线路长13m.
化曲为直
转化思想
两点之间
线段最短
A
B
D
C
归纳总结
A
B
B
A
C
D
E
12
1
5
化曲为直
A
B
C
55cm
48cm
B
A
55cm
6cm
10cm
化折为直
A
B
B
A
C
D
E
12
1
5
化曲为直
几何体的最短路径问题
转化思想
实质:两点之间线段最短
关键:实际问题转化数学问题
拓展延伸
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小虫爬行的最短路线长。
使PA+PG的值最小
“将军饮马”问题
转 化
拓展延伸
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小动物爬行的最短路线长。
使PA+PG的值最小
此时:PA+PG=PA′+PG
=A′G
60
20
60
拓展延伸
如图,长方体的透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深为AE=40cm,在水面上紧贴内壁G处有一鱼饵,G在水面线EF上,且EG=60cm;一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵,求小虫爬行的最短路线长。
60
20
60
解:如图,作点A关于BC的对称点A′,连接A′G交BC于点P,连接PA、PG,小虫沿着A→P→G的路线爬行时路线长最短,即此时PA+PG的值最小.
由题意知:
AE=40cm EG=60cm
∠A′EG=90°
在Rt△ A ′EG中:
A′E2+EG2 = A′G2
∴ 802 + 602 = A′G2
解得A′G=100
即小虫爬行的最短线路长100cm.
由作图知:A′B=AB=60cm
PA′=PA
∴ BE=AB-AE=20
∴ A′E= A′B+BE=80
∴ PA+PG=PA ′+PG=A′G
=100(cm)
课堂小结
勾
股
定
理
多边形的
折叠问题
几何体的
最短路径
+
+
实质:多边形的全等
关键:用好重合的线段和角
实质:两点之间线段最短
关键:实际问题转化数学问题
方程
思想
转化
思想
课后作业
1、如图所示,有一块直角三角形纸片,∠C=90 ,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则BD的长为________.
2、如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上。若AD=3,DE=1,则AB=_________.
(第1题图)
(第2题图)
课后作业
3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是________.
4、葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎藤常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,如图,它的底面周长是50cm,当一段葛藤绕树干均匀盘旋2圈升高为2.4m时,这段葛藤的长是_________.
A
B
(第3题图)
(第4题图)
课后作业
1、如图所示,有一块直角三角形纸片,∠C=90 ,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则BD的长为________.
2、如图,已知E为长方形纸片ABCD的边CD上一点,将纸片沿AE对折,点D的对应点D′恰好在线段BE上。若AD=3,DE=1,则AB=_________.
(第1题图)
(第2题图)
课后作业
3、如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是________.
4、葛藤是一种多年生草本植物,为获得更多的雨露和阳光,其茎藤常绕着附近的树干沿最短路线盘旋而上.如果把树干看成圆柱体,如图,它的底面周长是50cm,当一段葛藤绕树干均匀盘旋2圈升高为2.4m时,这段葛藤的长是_________.
A
B
(第3题图)
(第4题图)
