2021—2022学年人教版数学八年级下册17.1勾股定理 教学课件(共18张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学八年级下册17.1勾股定理 教学课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 728.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览


文档简介
(共18张PPT)
人教版八年级数学下册
《勾股定理》
2500年前,毕达哥拉斯在一次朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系。
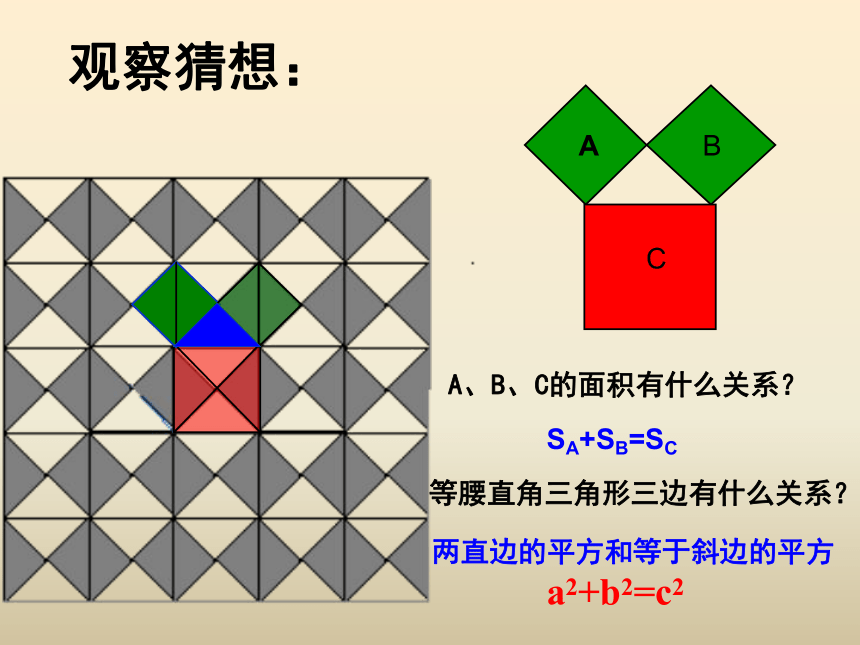
观察猜想:
A、B、C的面积有什么关系?
等腰直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
a2+b2=c2
A
B
C
A
B
C
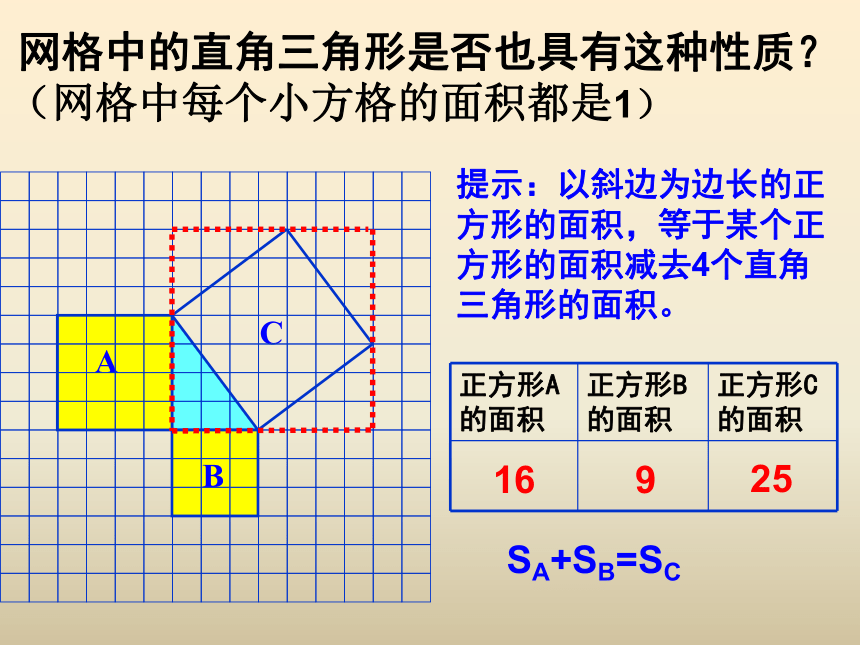
网格中的直角三角形是否也具有这种性质? (网格中每个小方格的面积都是1)
正方形A的面积 正方形B的面积 正方形C的面积
16
25
9
提示:以斜边为边长的正方形的面积,等于某个正方形的面积减去4个直角三角形的面积。
SA+SB=SC
A
B
C
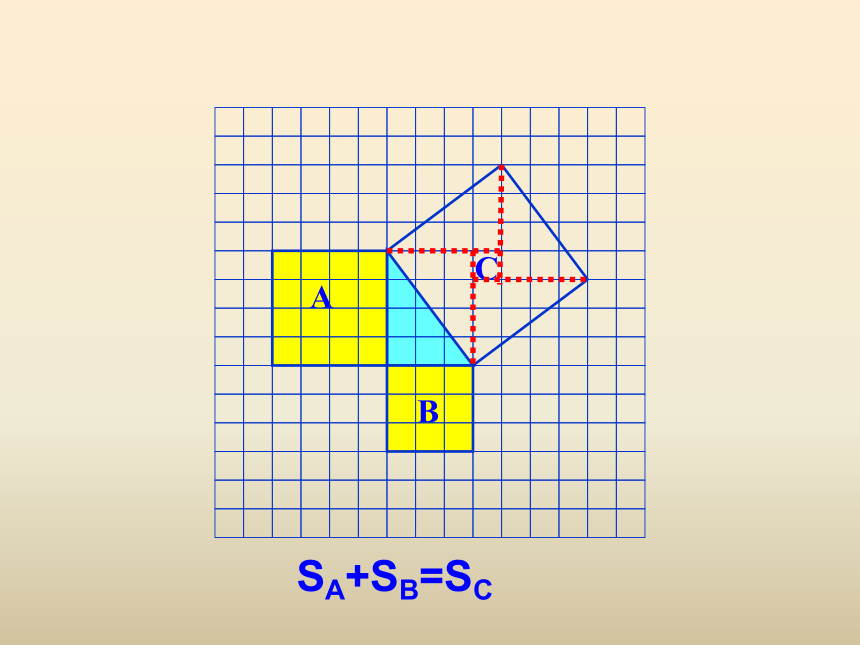
SA+SB=SC
A
B
C
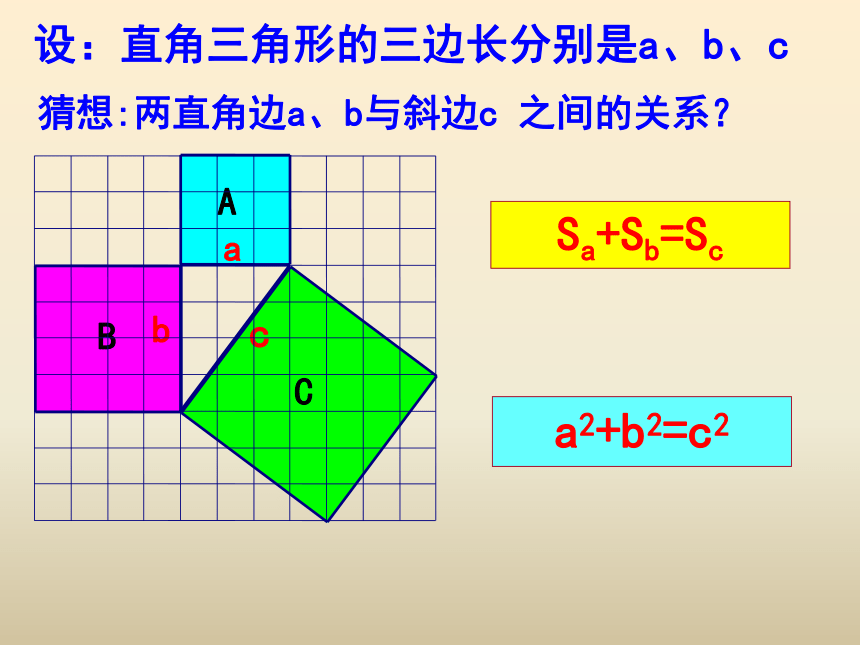
a
c
b
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
a2+b2=c2
a
c
b
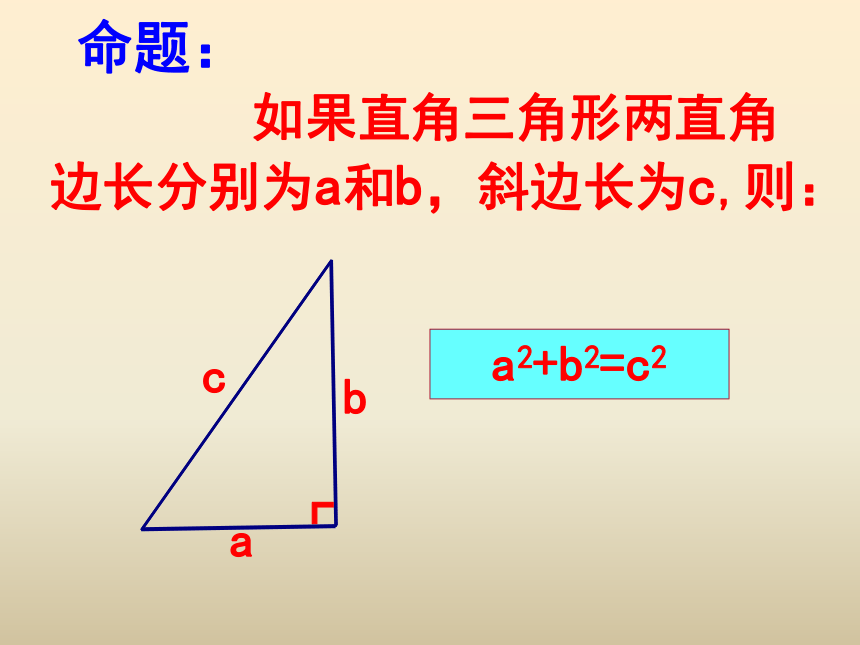
命题: 如果直角三角形两直角边长分别为a和b,斜边长为c,则:
a
c
b
a
b
c
思考:大正方形面积怎么求?
操作论证:
结论:
a
b
c
a
b
c
思考:大正方形面积怎么求?
结论:
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
勾股定理
(毕达哥拉斯定理)
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
学以致用,做一做:
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
3.求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
4.如图,在Rt△ABC中, ∠A=30°,AB=2,则BC= ___AC=___
C
A
B
1
3
√
合作探究:
一个门框尺寸如图所示,一块长6m,宽4.8m的薄木板能否从门框内通过?为什么?
3m
4m
⒈ 勾股定理揭示了直角三角形三边之间的数量关系。
⒉勾股定理: 直角三角形两直角边a、b的平方和,等于斜边c的平方。
a2+b2 =c2
⒊勾股定理的主要作用是:在直角三角形中,已知任意两边求第三边的长。
作业:
习题17.1第1、2题。
谢谢,再见!
人教版八年级数学下册
《勾股定理》
2500年前,毕达哥拉斯在一次朋友家做客时,发现朋友家用砖铺成的地面中反映了直角三角形三边的某种数量关系。
观察猜想:
A、B、C的面积有什么关系?
等腰直角三角形三边有什么关系?
SA+SB=SC
两直边的平方和等于斜边的平方
a2+b2=c2
A
B
C
A
B
C
网格中的直角三角形是否也具有这种性质? (网格中每个小方格的面积都是1)
正方形A的面积 正方形B的面积 正方形C的面积
16
25
9
提示:以斜边为边长的正方形的面积,等于某个正方形的面积减去4个直角三角形的面积。
SA+SB=SC
A
B
C
SA+SB=SC
A
B
C
a
c
b
Sa+Sb=Sc
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系?
a2+b2=c2
┏
a2+b2=c2
a
c
b
命题: 如果直角三角形两直角边长分别为a和b,斜边长为c,则:
a
c
b
a
b
c
思考:大正方形面积怎么求?
操作论证:
结论:
a
b
c
a
b
c
思考:大正方形面积怎么求?
结论:
┏
a2+b2=c2
a
c
b
直角三角形两直角边的平方和等于斜边的平方。
勾
股
弦
勾股定理
(毕达哥拉斯定理)
8
15
A
49
B
25
1.求下列图中字母所代表的正方形的面积:
学以致用,做一做:
2.求下列图中表示边的未知数x、y、z的值.
①
81
144
x
y
z
②
③
625
576
144
169
3.求下列直角三角形中未知边的长:
8
x
17
16
20
x
12
5
x
4.如图,在Rt△ABC中, ∠A=30°,AB=2,则BC= ___AC=___
C
A
B
1
3
√
合作探究:
一个门框尺寸如图所示,一块长6m,宽4.8m的薄木板能否从门框内通过?为什么?
3m
4m
⒈ 勾股定理揭示了直角三角形三边之间的数量关系。
⒉勾股定理: 直角三角形两直角边a、b的平方和,等于斜边c的平方。
a2+b2 =c2
⒊勾股定理的主要作用是:在直角三角形中,已知任意两边求第三边的长。
作业:
习题17.1第1、2题。
谢谢,再见!
