《函数y=Asin(ωx+φ)的图像》ppt课件
文档属性
| 名称 | 《函数y=Asin(ωx+φ)的图像》ppt课件 |  | |
| 格式 | zip | ||
| 文件大小 | 345.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-26 18:38:28 | ||
图片预览




文档简介
课件27张PPT。1.5函数 y=Asin(?x+?) 的图象 教学重点、难点:
重点:用参数思想讨论函数y=Asin(ωx+ )
的图象变换过程 。
难点:图像变换与函数解析式变换的
内在联系的认识 。 教学目的:
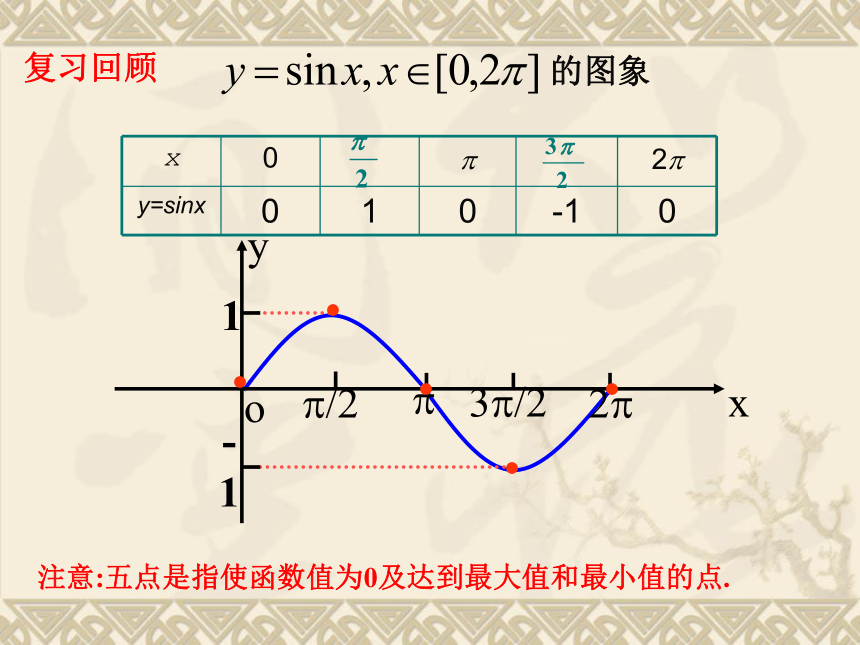
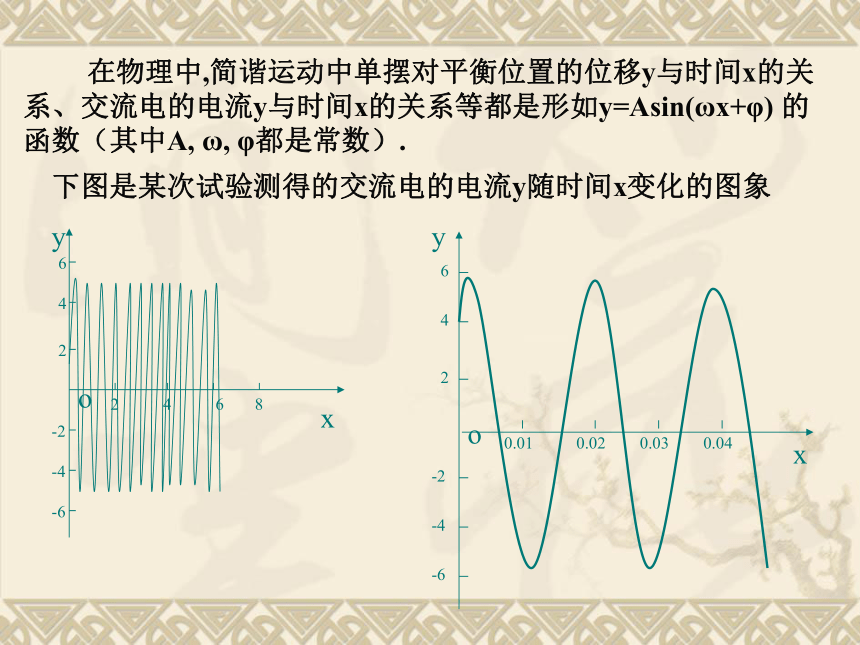
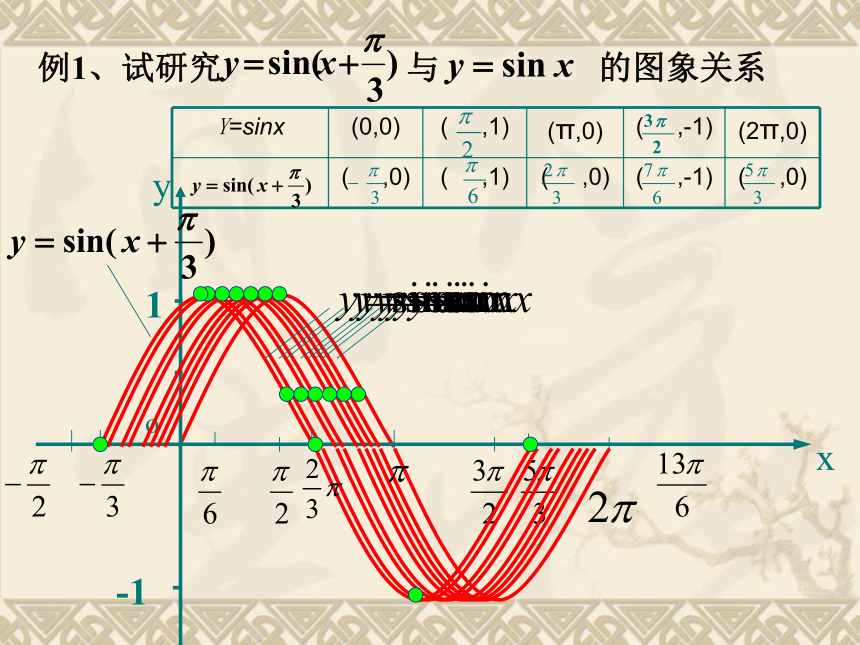
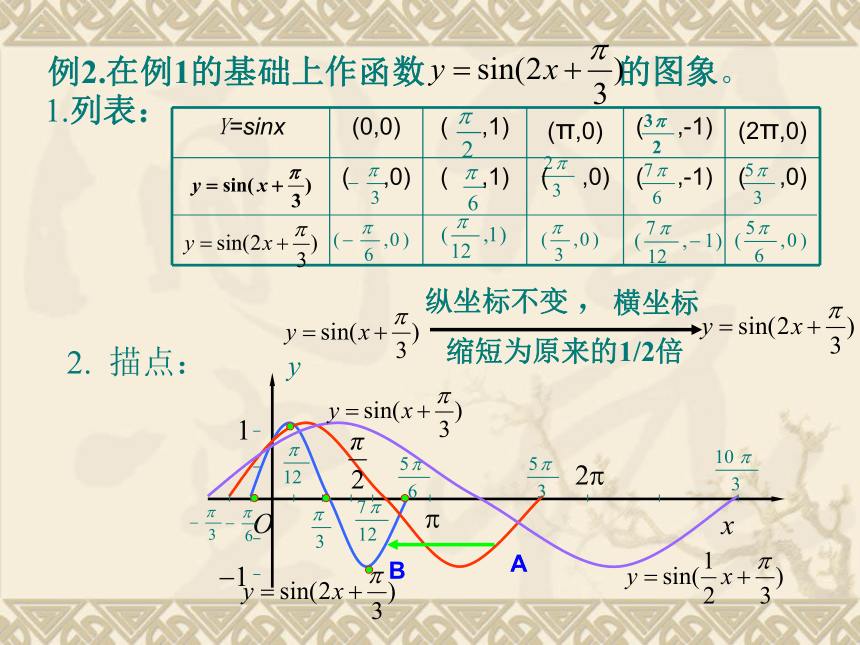
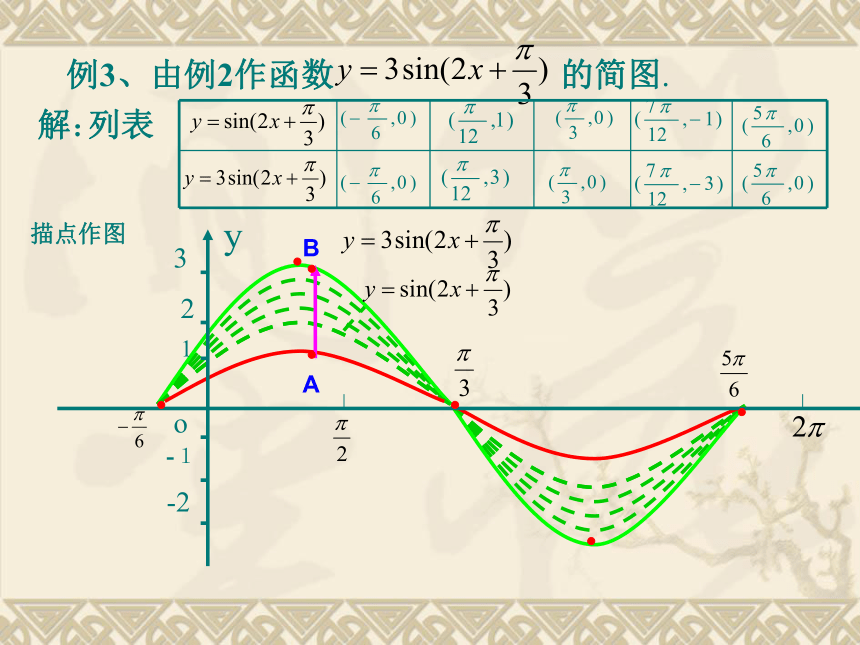
结合具体实例,了解y=Asin(ωx+ )的实际意义;能借助计算器或计算机画出y=Asin(ωx+ )的图象 ,观察参数A、ω、 对函数图像的影响。.....的图象注意:五点是指使函数值为0及达到最大值和最小值的点.复习回顾 在物理中,简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y=Asin(ωx+φ) 的函数(其中A, ω, φ都是常数).下图是某次试验测得的交流电的电流y随时间x变化的图象例1、试研究 与 的图象关系1-1 函数y=sin(x+ )( ≠0)的图象可以看作是把y=sinx的图象上所有的点向左(当 >0时 )或向右(当 <0时 )平行移动 个单位而得到的。1.列表:例2.在例1的基础上作函数 的图象。 xOy?2?1?12. 描点:AB 函数y=sin?x (? >0且?≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当00, ?>0) 的图象可由y=sinx经过如下变换得到:y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)注:余弦型函数 y=Acos(?x+?) 的相关问题同样处理。小结:1、作正弦型函数y=Asin(?x+?) 的图象的方法:
(1)用“五点法”作图;
(2)利用变换关系作图。2、函数 y = sinx 的图象与函数 y=Asin(?x+?)的图象间的变换关系。3、余弦型函数 y=Acos(?x+?) 的相关问题同样处理。y = sin(?x+?)y=sin(x+?)y = sinxy=Asin(?x+?)
作业:
课本58页第二题,并写出其图像
怎样由y=sinx的图像变化得到。1、将函数 y= sinx 的图象向左平移 π/ 6 得到的曲线对应的解析式为( )
A. y=sin(x+π/6) B. y=sin(x-π/6)
C. y=sin(x+π/3) D. y=sin(x-π/3)
2、要得到函数 y = cosx 的图象,只需将函数 y = cos (x-π/ 6) 的图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移1/6个单位 D. 向右平移1/6个单位
3、函数 y = 3sin( x/ 2 + π/3) 的图象可由函数 y = 3 sin x 经( )变换而得;
A.????先把横坐标扩大到原来的两倍(纵坐标不变) ,再向左平移π/6个单位
B.???先把横坐标缩短到原来的1/2倍(纵坐标不变) ,再向右平移π/3个单位
C.???先向右平移π/3个单位 ,再把横坐标缩短到原来的1/2倍(纵坐标不变)
D.??? 先向左平移π/3个单位 ,再把横坐标扩大到原来的两倍(纵坐标不变)
*4、要得到函数 y = cos ( 2x -π/4) 的图象,只需将函数 y = cos 2 x 的图象( )
A. 向左平移π/4个单位 B. 向右平移π / 4 个单位
C. 向左平移π/ 8个单位 D. 向右平移π/ 8个单位 AADC自我检测:谢谢大家
重点:用参数思想讨论函数y=Asin(ωx+ )
的图象变换过程 。
难点:图像变换与函数解析式变换的
内在联系的认识 。 教学目的:
结合具体实例,了解y=Asin(ωx+ )的实际意义;能借助计算器或计算机画出y=Asin(ωx+ )的图象 ,观察参数A、ω、 对函数图像的影响。.....的图象注意:五点是指使函数值为0及达到最大值和最小值的点.复习回顾 在物理中,简谐运动中单摆对平衡位置的位移y与时间x的关系、交流电的电流y与时间x的关系等都是形如y=Asin(ωx+φ) 的函数(其中A, ω, φ都是常数).下图是某次试验测得的交流电的电流y随时间x变化的图象例1、试研究 与 的图象关系1-1 函数y=sin(x+ )( ≠0)的图象可以看作是把y=sinx的图象上所有的点向左(当 >0时 )或向右(当 <0时 )平行移动 个单位而得到的。1.列表:例2.在例1的基础上作函数 的图象。 xOy?2?1?12. 描点:AB 函数y=sin?x (? >0且?≠1)的图象可以看作是把 y=sinx 的图象上所有点的横坐标缩短(当?>1时)或伸长(当00, ?>0) 的图象可由y=sinx经过如下变换得到:y=sinxy=sin(x+?)y=sin(?x+?)y=Asin(?x+?)注:余弦型函数 y=Acos(?x+?) 的相关问题同样处理。小结:1、作正弦型函数y=Asin(?x+?) 的图象的方法:
(1)用“五点法”作图;
(2)利用变换关系作图。2、函数 y = sinx 的图象与函数 y=Asin(?x+?)的图象间的变换关系。3、余弦型函数 y=Acos(?x+?) 的相关问题同样处理。y = sin(?x+?)y=sin(x+?)y = sinxy=Asin(?x+?)
作业:
课本58页第二题,并写出其图像
怎样由y=sinx的图像变化得到。1、将函数 y= sinx 的图象向左平移 π/ 6 得到的曲线对应的解析式为( )
A. y=sin(x+π/6) B. y=sin(x-π/6)
C. y=sin(x+π/3) D. y=sin(x-π/3)
2、要得到函数 y = cosx 的图象,只需将函数 y = cos (x-π/ 6) 的图象( )
A. 向左平移π/6个单位 B. 向右平移π/6个单位
C. 向左平移1/6个单位 D. 向右平移1/6个单位
3、函数 y = 3sin( x/ 2 + π/3) 的图象可由函数 y = 3 sin x 经( )变换而得;
A.????先把横坐标扩大到原来的两倍(纵坐标不变) ,再向左平移π/6个单位
B.???先把横坐标缩短到原来的1/2倍(纵坐标不变) ,再向右平移π/3个单位
C.???先向右平移π/3个单位 ,再把横坐标缩短到原来的1/2倍(纵坐标不变)
D.??? 先向左平移π/3个单位 ,再把横坐标扩大到原来的两倍(纵坐标不变)
*4、要得到函数 y = cos ( 2x -π/4) 的图象,只需将函数 y = cos 2 x 的图象( )
A. 向左平移π/4个单位 B. 向右平移π / 4 个单位
C. 向左平移π/ 8个单位 D. 向右平移π/ 8个单位 AADC自我检测:谢谢大家
