2021-2022学年青岛版数学八年级下册6.1平行四边形及其性质课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版数学八年级下册6.1平行四边形及其性质课时练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 464.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 12:01:27 | ||
图片预览


文档简介
2022年青岛版数学八年级下册
6.1《平行四边形及其性质》课时练习
一、选择题
1.若平行四边形中两个内角的度数比为1∶3,则其中较小的内角是( )
A.30° B.45° C.60° D.75°
2.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=35°,则∠BCE的度数为( )
A.53° B.37° C.47° D.123°
3.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为 ( )
A.13 B.17 C.20 D.26
4.如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F.若 ABCD的周长为18,OE=1.5,则四边形EFCD的周长为 ( )
A.14 B.13 C.12 D.10
5.已知□ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A.∠DAE=∠BAE B.2∠DEA= ∠DAB C.DE=BE D.BC=DE
6.如图,在□ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,□ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
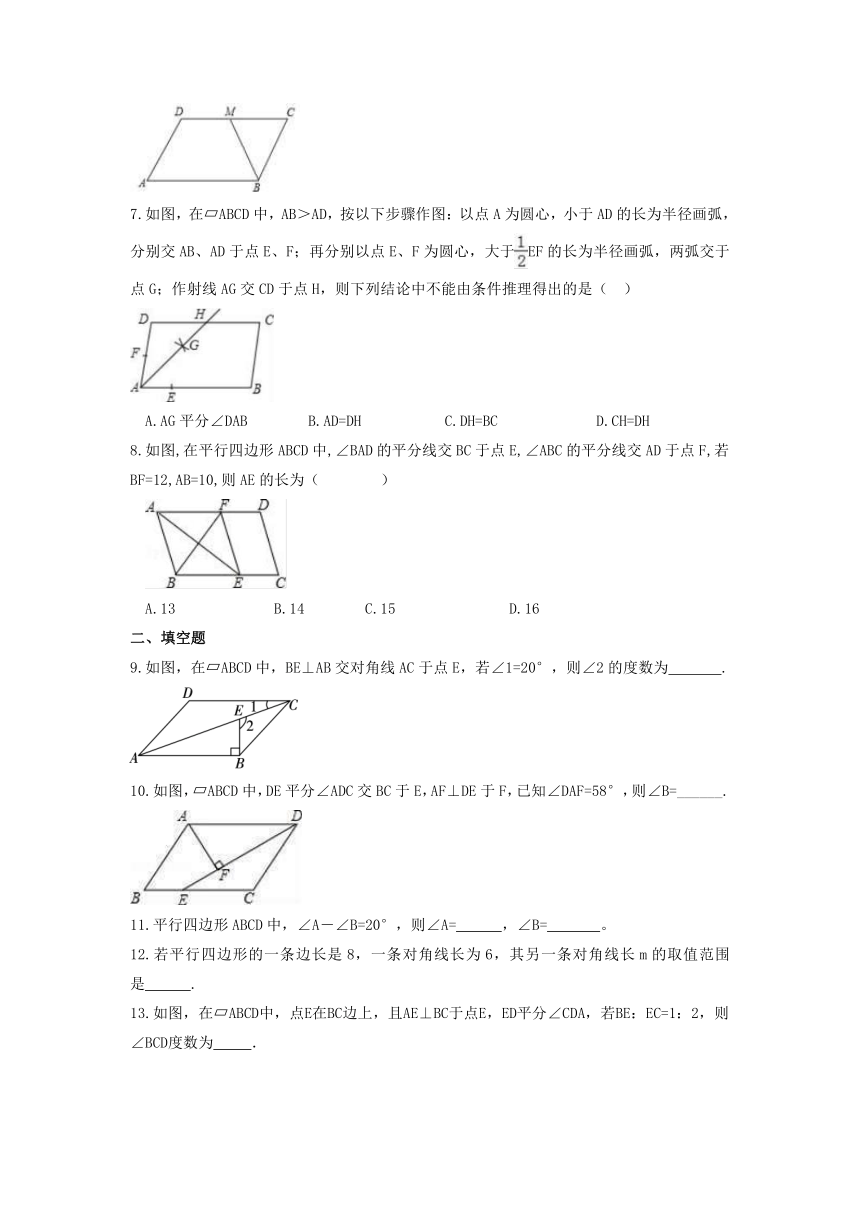
7.如图,在 ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
A.AG平分∠DAB B.AD=DH C.DH=BC D.CH=DH
8.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A.13 B.14 C.15 D.16
二、填空题
9.如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 .
10.如图, ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=______.
11.平行四边形ABCD中,∠A-∠B=20°,则∠A= ,∠B= 。
12.若平行四边形的一条边长是8,一条对角线长为6,其另一条对角线长m的取值范围是 .
13.如图,在 ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD度数为 .
14.如图,第1个图形中一共有1个平行四边形,第2个图形中一共有5个平行四边形,第3个图形中一共有11个平行四边形,…则第n个图形中平行四边形的个数是 .
三、解答题
15.如图,在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25°,求∠C、∠B的度数。
16.如图,□ABCD的周长为60cm,△AOB的周长比△BOC大8cm,求AB、BC的长。
17.如图,已知在 ABCD中,E、F是对角线BD上的两点,且BF=DE.
求证:AE=CF.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,MN是过O点的直线,交BC于M,交AD于N,BM=2,AN=2.8,求BC和AD的长.
参考答案
1.B;
2.B.
3.B
4.C
5.C.
6.C
7.D
8.D
9.答案为:110°.
10.答案为:64°.
11.答案为:100°,80°;
12.答案为:10<m<22;
13.答案为:120°.
14.答案为:n2+n﹣1.
15.解:∵∠BAD的平分线AE交DC于E,若∠DAE=25°,
∴∠BAD=50°。
∴在平行四边形ABCD中:
∠C=∠BAD=50°,∠B=180°-∠C=130°。
16.解:∵□ABCD的周长为60cm,
∴BC+AB=30cm,①
又∵△AOB的周长比△BOC的周长大8cm,
∴AB-BC=8cm,②
由①②得:AB=19cm,BC=11cm。
故答案为:19cm,11cm。
17.证明:连接AC交BD于点O,连接AF、CE
∵ ABCD
∴OA=OC,OB=OD
∵OF=BF﹣OB,OE=DE﹣OD,BF=DE
∴OE=OF
∵OA=OC,OE=OF
∴四边形AECF是平行四边形
∴AE=CF.
18.解:在平行四边新ABCD中,
∵对角线AC,BD相交于点O,MN是过O点的直线,
∴AN=MC DN=BM
∵BC=BM+MC
∴BC=BM+AN=2+2.8=4.8
∵AD=BC
∴AD=4.8
6.1《平行四边形及其性质》课时练习
一、选择题
1.若平行四边形中两个内角的度数比为1∶3,则其中较小的内角是( )
A.30° B.45° C.60° D.75°
2.如图,在平行四边形ABCD中,过点C的直线CE⊥AB,垂足为E,若∠EAD=35°,则∠BCE的度数为( )
A.53° B.37° C.47° D.123°
3.如图, ABCD的对角线AC,BD交于点O,已知AD=8,BD=12,AC=6,则△OBC的周长为 ( )
A.13 B.17 C.20 D.26
4.如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F.若 ABCD的周长为18,OE=1.5,则四边形EFCD的周长为 ( )
A.14 B.13 C.12 D.10
5.已知□ABCD,根据图中尺规作图的痕迹,判断下列结论中不一定成立的是( )
A.∠DAE=∠BAE B.2∠DEA= ∠DAB C.DE=BE D.BC=DE
6.如图,在□ABCD中,BM是∠ABC的平分线交CD于点M,且MC=2,□ABCD的周长是14,则DM等于( )
A.1 B.2 C.3 D.4
7.如图,在 ABCD中,AB>AD,按以下步骤作图:以点A为圆心,小于AD的长为半径画弧,分别交AB、AD于点E、F;再分别以点E、F为圆心,大于EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H,则下列结论中不能由条件推理得出的是( )
A.AG平分∠DAB B.AD=DH C.DH=BC D.CH=DH
8.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A.13 B.14 C.15 D.16
二、填空题
9.如图,在 ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 .
10.如图, ABCD中,DE平分∠ADC交BC于E,AF⊥DE于F,已知∠DAF=58°,则∠B=______.
11.平行四边形ABCD中,∠A-∠B=20°,则∠A= ,∠B= 。
12.若平行四边形的一条边长是8,一条对角线长为6,其另一条对角线长m的取值范围是 .
13.如图,在 ABCD中,点E在BC边上,且AE⊥BC于点E,ED平分∠CDA,若BE:EC=1:2,则∠BCD度数为 .
14.如图,第1个图形中一共有1个平行四边形,第2个图形中一共有5个平行四边形,第3个图形中一共有11个平行四边形,…则第n个图形中平行四边形的个数是 .
三、解答题
15.如图,在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25°,求∠C、∠B的度数。
16.如图,□ABCD的周长为60cm,△AOB的周长比△BOC大8cm,求AB、BC的长。
17.如图,已知在 ABCD中,E、F是对角线BD上的两点,且BF=DE.
求证:AE=CF.
18.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,MN是过O点的直线,交BC于M,交AD于N,BM=2,AN=2.8,求BC和AD的长.
参考答案
1.B;
2.B.
3.B
4.C
5.C.
6.C
7.D
8.D
9.答案为:110°.
10.答案为:64°.
11.答案为:100°,80°;
12.答案为:10<m<22;
13.答案为:120°.
14.答案为:n2+n﹣1.
15.解:∵∠BAD的平分线AE交DC于E,若∠DAE=25°,
∴∠BAD=50°。
∴在平行四边形ABCD中:
∠C=∠BAD=50°,∠B=180°-∠C=130°。
16.解:∵□ABCD的周长为60cm,
∴BC+AB=30cm,①
又∵△AOB的周长比△BOC的周长大8cm,
∴AB-BC=8cm,②
由①②得:AB=19cm,BC=11cm。
故答案为:19cm,11cm。
17.证明:连接AC交BD于点O,连接AF、CE
∵ ABCD
∴OA=OC,OB=OD
∵OF=BF﹣OB,OE=DE﹣OD,BF=DE
∴OE=OF
∵OA=OC,OE=OF
∴四边形AECF是平行四边形
∴AE=CF.
18.解:在平行四边新ABCD中,
∵对角线AC,BD相交于点O,MN是过O点的直线,
∴AN=MC DN=BM
∵BC=BM+MC
∴BC=BM+AN=2+2.8=4.8
∵AD=BC
∴AD=4.8
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
