2021-2022学年人教版数学七年级下册5.1.2垂线课件(23张)
文档属性
| 名称 | 2021-2022学年人教版数学七年级下册5.1.2垂线课件(23张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 941.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览




文档简介
(共23张PPT)
5.1.2 垂线
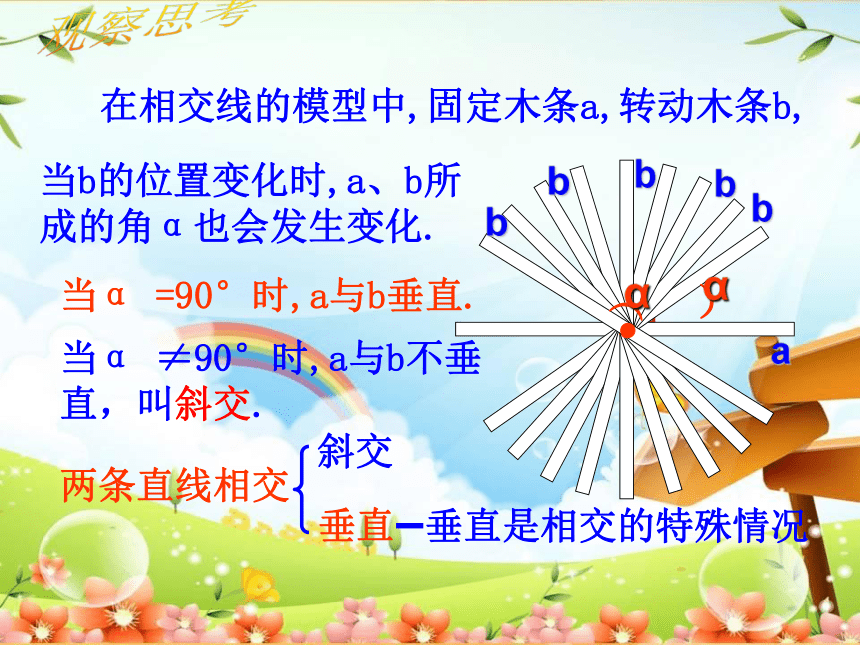
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
观察思考
)
α
a
b
b
b
b
b
)
α
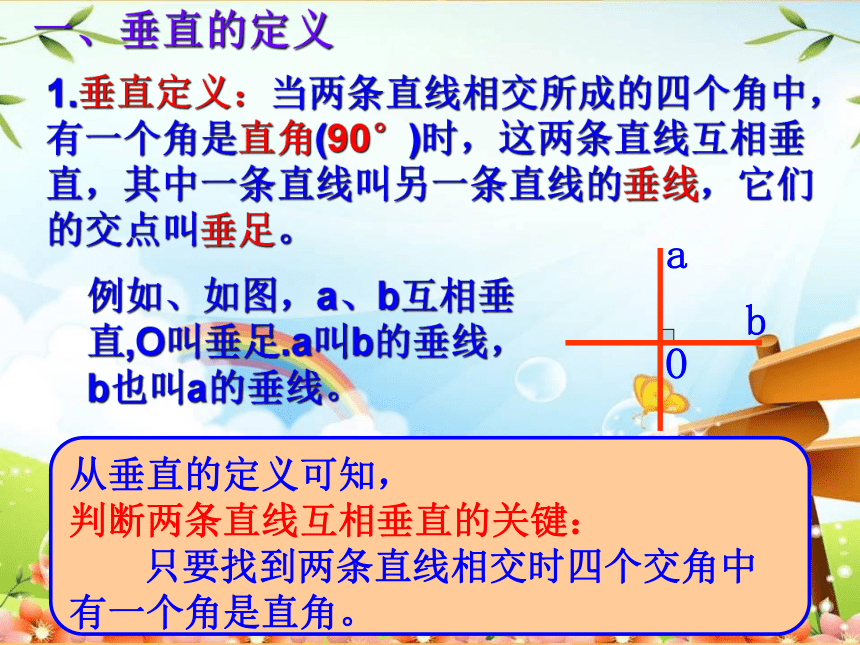
1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角(90°)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。
b
a
O
一、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中有一个角是直角。
b
a
用“⊥”和直线字母表示垂直
O
α
2.垂直的表示:
例如、如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b, 垂足为O.
或a⊥b于O.
F
E
M
N
O
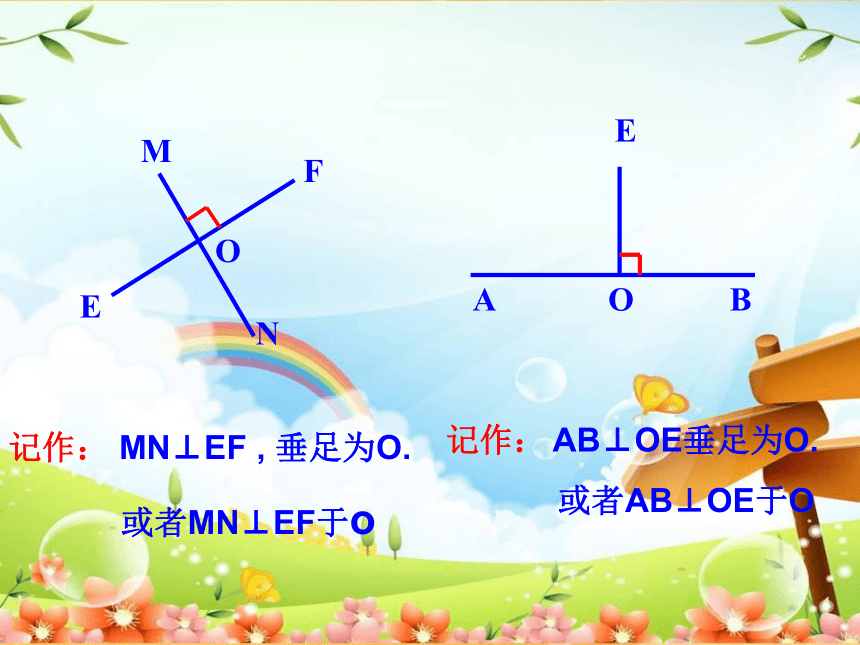
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于o
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程可以写成:
A
B
C
D
O
3.垂直的书写形式:
1、下面四种判定两条直线垂直的方法,正确的有
( )个
(1)两条直线相交所成的四个角中有一个角是直角,
则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这
两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直
线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条
直线互相垂直
(A) 4 (B) 3
(C) 2 (D) 1
A
例题:
b
a
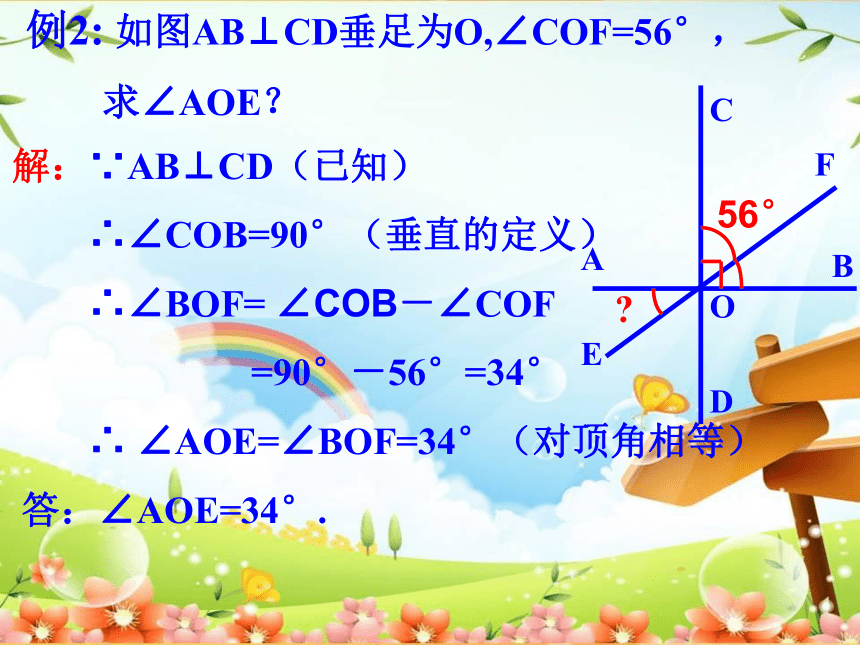
例2: 如图AB⊥CD垂足为O,∠COF=56°,
求∠AOE?
解:∵AB⊥CD(已知)
∴∠COB=90°(垂直的定义)
∴∠BOF= ∠COB-∠COF
=90°-56°=34°
∴ ∠AOE=∠BOF=34°(对顶角相等)
答:∠AOE=34°.
F
E
D
C
B
A
O
56°
1.垂线的画法:
问题:
这样画m的垂线可以画几条?
1靠、
2画线
m
O
如图,已知直线 m,作m的垂线。
工具:三角板(或量角器)
A
无数条
1.垂线的画法:
m
A
如图,已知直线m和m上的一点A ,作m的垂线.
B
3画线:沿着三角板的另一直角边画出垂线.
2移:移动三角板到已知点;
1靠:把三角板的一直角边靠在直线上;
则所画直线AB是过点A的直线m的垂线.
1.垂线的画法:
m
A
如图,已知直线 m 和m外的一点A ,作m的垂线.
B
则所画直线AB是过点A的直线m的垂线.
思考:
结论:在同一平面内,过一点有且只有一条直线与已知直线垂直。
(1)画已知直线m的垂线能画几条
(2)过直线m上的一点A画m的垂线,这样的
垂线能画几条
(3)过直线m外的一点A画m的垂线,这样的
垂线能画几条
垂线的性质
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
问题:
(1)“过一点”包括几种情况?
(2)“有且只有”是什么意思?
直线上的一点
直线外的一点
有: 存在性
只有:唯一性
2. 过点P作线段或射线所在直线的垂线
A
B
.
.
.P
(1)
.
O
.P
.A
(2)
注意:过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线的性质2
垂线段
斜线段
∵PB⊥m于B
∴PB垂线段是垂线上的一部分,它是线段,一端是一个点,另一端是垂足。
A
B
P
D
特别强调:
垂线
垂线段
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
m
A
例如:如图,PA⊥m于点A ,垂线段PA的长度叫做点P到直线m的距离.
例:如图,是一个同学跳远的位置,跳远成绩怎么表示
m
P
A
解:过P点作PA⊥m于点A,
垂线段PA的长度就是
该同学的跳远成绩.
点到直线的距离的概念:
B
如图,怎样测量 点A 到 直线 m 的距离?
A
m
1.过点A画出直线m的垂线段AB,垂足为B;
2.用刻度尺量出垂线段AB的长度.
0m
20m
30m
10m
C
A
B
0m
20m
30m
10m
0m
20m
30m
10m
8m
25m
例1、如图,量出(1)村庄A与货场B的距离,
(2)货场B到铁道的距离。
0cm
20cm
30cm
10cm
例2、如图,
(1)画出线段BC的中点M,连结AM;
(2)比较点B与点C到直线AM的距离。
A
B
C
M
P
Q
0cm
20cm
30cm
10cm
0cm
20cm
30cm
10cm
9cm
9cm
∴BP=CQ
1、垂直的概念:
如果两条直线相交所成的四个角中,有一个是直角,就说这两条直线互相垂直.
小结:
2、垂线的性质1:
同一平面内,经过一点有且只有一条直线与已知直线垂直.
4、能过一点作出直线(或线段、
射线)的垂线
3 、画垂线的方法:
用工具(量角器、三角板)
不用工具(“折”)
回忆两条直线相交这部分知识,你能够把它们画成一个知识结构图吗?
小结
5.1.2 垂线
在相交线的模型中,固定木条a,转动木条b,
当α =90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α ≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
观察思考
)
α
a
b
b
b
b
b
)
α
1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角(90°)时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。
b
a
O
一、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中有一个角是直角。
b
a
用“⊥”和直线字母表示垂直
O
α
2.垂直的表示:
例如、如图,a、b互相垂直, 垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b, 垂足为O.
或a⊥b于O.
F
E
M
N
O
记作: MN⊥EF , 垂足为O.
或者MN⊥EF于o
A
B
O
E
记作: AB⊥OE垂足为O.
或者AB⊥OE于O
∵∠AOC=90°(已知),
∴AB⊥CD(垂直的定义).
如果直线AB、CD 相交于点O,∠AOC=90°
(或其它三个角中的一个角等于90°),那么 AB⊥CD.
这个推理过程可以写成:
∵AB⊥CD(已知),
∴∠AOC=90°(垂直的定义).
如果AB⊥CD,那么所得的四个角中,必有一个是直角. 这个推理过程可以写成:
A
B
C
D
O
3.垂直的书写形式:
1、下面四种判定两条直线垂直的方法,正确的有
( )个
(1)两条直线相交所成的四个角中有一个角是直角,
则这两条直线互相垂直
(2)两条直线相交,只要有一组邻补角相等,则这
两条直线互相垂直
(3)两条直线相交,所成的四个角相等,这两条直
线互相垂直
(4)两条直线相交,有一组对顶角互补,则这两条
直线互相垂直
(A) 4 (B) 3
(C) 2 (D) 1
A
例题:
b
a
例2: 如图AB⊥CD垂足为O,∠COF=56°,
求∠AOE?
解:∵AB⊥CD(已知)
∴∠COB=90°(垂直的定义)
∴∠BOF= ∠COB-∠COF
=90°-56°=34°
∴ ∠AOE=∠BOF=34°(对顶角相等)
答:∠AOE=34°.
F
E
D
C
B
A
O
56°
1.垂线的画法:
问题:
这样画m的垂线可以画几条?
1靠、
2画线
m
O
如图,已知直线 m,作m的垂线。
工具:三角板(或量角器)
A
无数条
1.垂线的画法:
m
A
如图,已知直线m和m上的一点A ,作m的垂线.
B
3画线:沿着三角板的另一直角边画出垂线.
2移:移动三角板到已知点;
1靠:把三角板的一直角边靠在直线上;
则所画直线AB是过点A的直线m的垂线.
1.垂线的画法:
m
A
如图,已知直线 m 和m外的一点A ,作m的垂线.
B
则所画直线AB是过点A的直线m的垂线.
思考:
结论:在同一平面内,过一点有且只有一条直线与已知直线垂直。
(1)画已知直线m的垂线能画几条
(2)过直线m上的一点A画m的垂线,这样的
垂线能画几条
(3)过直线m外的一点A画m的垂线,这样的
垂线能画几条
垂线的性质
垂线的性质1:在同一平面内,过一点有且只有一条直线与已知直线垂直.
问题:
(1)“过一点”包括几种情况?
(2)“有且只有”是什么意思?
直线上的一点
直线外的一点
有: 存在性
只有:唯一性
2. 过点P作线段或射线所在直线的垂线
A
B
.
.
.P
(1)
.
O
.P
.A
(2)
注意:过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
连接直线外一点与直线上各点的所有线段中,垂线段最短。
垂线段最短
P
A
B
C
m
D
简单说成:垂线段最短.
垂线的性质2
垂线段
斜线段
∵PB⊥m于B
∴PB
A
B
P
D
特别强调:
垂线
垂线段
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
m
A
例如:如图,PA⊥m于点A ,垂线段PA的长度叫做点P到直线m的距离.
例:如图,是一个同学跳远的位置,跳远成绩怎么表示
m
P
A
解:过P点作PA⊥m于点A,
垂线段PA的长度就是
该同学的跳远成绩.
点到直线的距离的概念:
B
如图,怎样测量 点A 到 直线 m 的距离?
A
m
1.过点A画出直线m的垂线段AB,垂足为B;
2.用刻度尺量出垂线段AB的长度.
0m
20m
30m
10m
C
A
B
0m
20m
30m
10m
0m
20m
30m
10m
8m
25m
例1、如图,量出(1)村庄A与货场B的距离,
(2)货场B到铁道的距离。
0cm
20cm
30cm
10cm
例2、如图,
(1)画出线段BC的中点M,连结AM;
(2)比较点B与点C到直线AM的距离。
A
B
C
M
P
Q
0cm
20cm
30cm
10cm
0cm
20cm
30cm
10cm
9cm
9cm
∴BP=CQ
1、垂直的概念:
如果两条直线相交所成的四个角中,有一个是直角,就说这两条直线互相垂直.
小结:
2、垂线的性质1:
同一平面内,经过一点有且只有一条直线与已知直线垂直.
4、能过一点作出直线(或线段、
射线)的垂线
3 、画垂线的方法:
用工具(量角器、三角板)
不用工具(“折”)
回忆两条直线相交这部分知识,你能够把它们画成一个知识结构图吗?
小结
