2021-2022学年青岛版数学八年级下册11.1图形的平移课时练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年青岛版数学八年级下册11.1图形的平移课时练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 261.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览


文档简介
2022年青岛版数学八年级下册
11.1《图形的平移》课时练习
一、选择题
1.下列四个图形中,不能通过基本图形平移得到的是( )
A. B. C. D.
2.下列图形可由平移得到的是( )
3.下列说法正确的是( )
A.一个图形平移后,它各点的横、纵坐标都发生变化
B.一个图形平移后,它的大小发生变化,形状不变
C.把一个图形沿y轴平移若干个单位长度后,与原图形相比各点的横坐标没有发生变化
D.图形平移后,一些点的坐标可以不发生变化
4.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
5.如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.7
6.如图,△ABC平移到△DEF的位置,则下列说法:
①AB∥DE,AD=CF=BE;
②∠ACB=∠DEF;
③平移的方向是点C到点E的方向;
④平移距离为线段BE的长.
其中说法正确的有( )
A.①② B.①④ C.②③ D.②④
7.如图所示的四图个中各有两个完全相同的三角形,如果其中一个三角形不动,移动另一个三角形,则能够通过平移使两个三角形重合的图形有( ).
A.①②③ B.①③④ C.①②④ D.①③
8.如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),
则(a﹣b)等于( )
A.3 B.4 C.5 D.6
二、填空题
9.如图所示,将△ABC平移到△A′B′C′的位置,连接BB′,AA′,CC′,平移的方向是点______到点________的方向,平移的距离是线段______的长度.
10.如图,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,则∠FDE= .
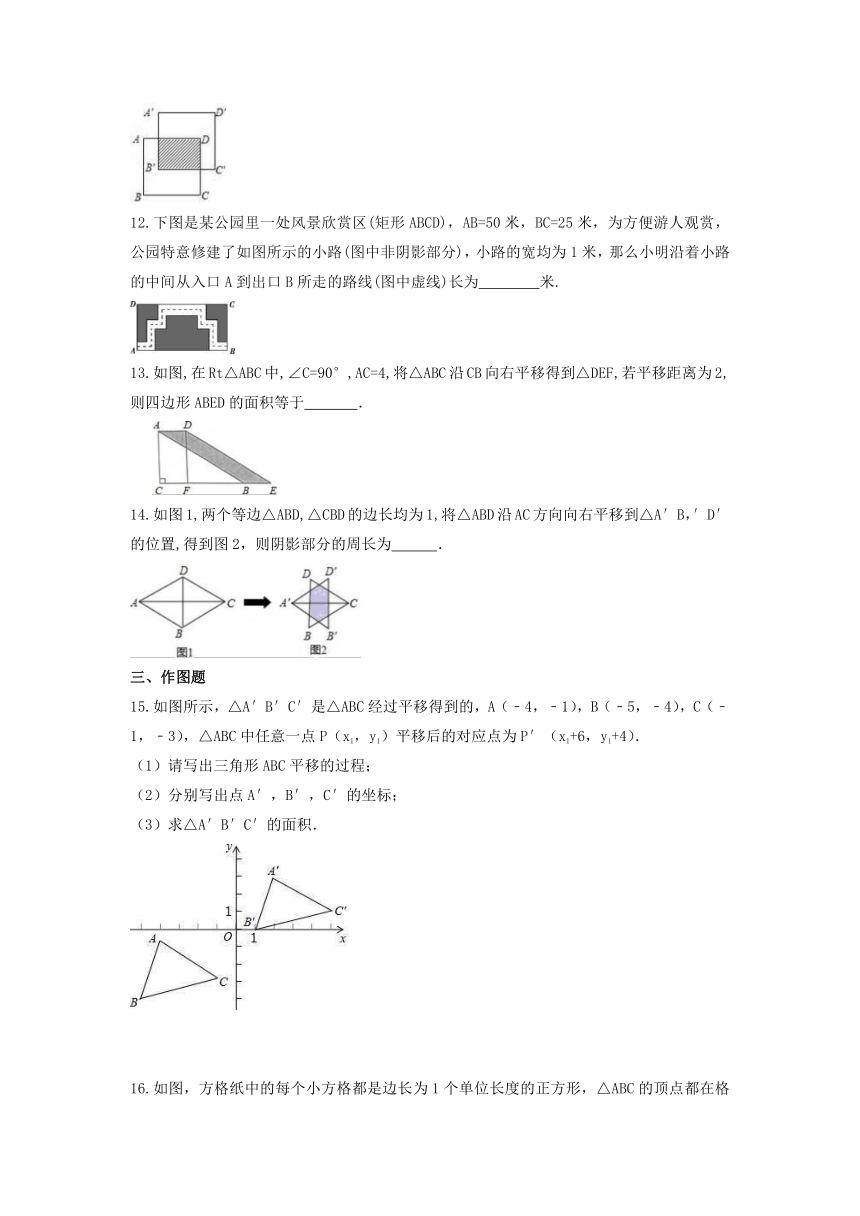
11.如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为______cm2.
12.下图是某公园里一处风景欣赏区(矩形ABCD),AB=50米,BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间从入口A到出口B所走的路线(图中虚线)长为 米.
13.如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED的面积等于 .
14.如图1,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B,′D′的位置,得到图2,则阴影部分的周长为 .
三、作图题
15.如图所示,△A′B′C′是△ABC经过平移得到的,A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.
16.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为 ,点C的坐标为 ;
(2)将△ABC向左平移7个单位,请画出平移后的△A′B′C′,若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M'的坐标为 .
17.如图,在边长均为1个单位的正方形网格图中,建立了直角坐标系xOy,按要求解答下列问题:
(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后的图形△A1B1C1;
(3)求△ABC的面积.
18.探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(3)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(4)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
参考答案
1.D.
2.A
3.C.
4.C
5.A.
6.B.
7.D
8.D.
9.答案为:A(B或C),A’(B’或C’) ,AA’(BB’或CC’)
10.答案为:70°;
11.答案为:6.
12.答案为:98
13.答案为:8.
14.答案为:2.
15.解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′
或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
(2)由(1)可知,A′(2,3),B′(1,0),C′(5,1);
(3)如图所示,S△A′B′C′=3×4﹣×1×3﹣×1×4﹣×2×3=5.5.
16.解:(1)利用图形得出:点A的坐标为:(2,8),点C的坐标为:(6,6);
故答案为:(2,8),(6,6);
(2)∵将△ABC向左平移7个单位,M为△ABC内的一点,其坐标为(a,b),
∴平移后点M的对应点M'的坐标为:(a﹣7,b).故答案为:(a﹣7,b).
17.解:(1)如图所示:A(﹣1,8),B(﹣5,3),C(0,6);
(2)如图所示:(3)△ABC的面积为:×(5+1)×5﹣×1×2﹣×3×5=6.5.
18.(1)相等,过E作AB的平行线即可;
(2)∠B+∠D+∠E=360°;
(3)∠B=∠D+∠E;(4)相等.
11.1《图形的平移》课时练习
一、选择题
1.下列四个图形中,不能通过基本图形平移得到的是( )
A. B. C. D.
2.下列图形可由平移得到的是( )
3.下列说法正确的是( )
A.一个图形平移后,它各点的横、纵坐标都发生变化
B.一个图形平移后,它的大小发生变化,形状不变
C.把一个图形沿y轴平移若干个单位长度后,与原图形相比各点的横坐标没有发生变化
D.图形平移后,一些点的坐标可以不发生变化
4.如图,将△ABE向右平移2cm得到△DCF,如果△ABE的周长是16cm,那么四边形ABFD的周长是( )
A.16cm B.18cm C.20cm D.21cm
5.如图,△ABC沿着由点B到点E的方向,平移到△DEF,已知BC=5.EC=3,那么平移的距离为( )
A.2 B.3 C.5 D.7
6.如图,△ABC平移到△DEF的位置,则下列说法:
①AB∥DE,AD=CF=BE;
②∠ACB=∠DEF;
③平移的方向是点C到点E的方向;
④平移距离为线段BE的长.
其中说法正确的有( )
A.①② B.①④ C.②③ D.②④
7.如图所示的四图个中各有两个完全相同的三角形,如果其中一个三角形不动,移动另一个三角形,则能够通过平移使两个三角形重合的图形有( ).
A.①②③ B.①③④ C.①②④ D.①③
8.如图,两个平行四边形的面积分别为18、12,两阴影部分的面积分别为a、b(a>b),
则(a﹣b)等于( )
A.3 B.4 C.5 D.6
二、填空题
9.如图所示,将△ABC平移到△A′B′C′的位置,连接BB′,AA′,CC′,平移的方向是点______到点________的方向,平移的距离是线段______的长度.
10.如图,三角形DEF平移得到三角形ABC,已知∠B=45°,∠C=65°,则∠FDE= .
11.如图,边长为4cm的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形A′B′C′D′,此时阴影部分的面积为______cm2.
12.下图是某公园里一处风景欣赏区(矩形ABCD),AB=50米,BC=25米,为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为1米,那么小明沿着小路的中间从入口A到出口B所走的路线(图中虚线)长为 米.
13.如图,在Rt△ABC中,∠C=90°,AC=4,将△ABC沿CB向右平移得到△DEF,若平移距离为2,则四边形ABED的面积等于 .
14.如图1,两个等边△ABD,△CBD的边长均为1,将△ABD沿AC方向向右平移到△A′B,′D′的位置,得到图2,则阴影部分的周长为 .
三、作图题
15.如图所示,△A′B′C′是△ABC经过平移得到的,A(﹣4,﹣1),B(﹣5,﹣4),C(﹣1,﹣3),△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4).
(1)请写出三角形ABC平移的过程;
(2)分别写出点A′,B′,C′的坐标;
(3)求△A′B′C′的面积.
16.如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标系.
(1)点A的坐标为 ,点C的坐标为 ;
(2)将△ABC向左平移7个单位,请画出平移后的△A′B′C′,若M为△ABC内的一点,其坐标为(a,b),则平移后点M的对应点M'的坐标为 .
17.如图,在边长均为1个单位的正方形网格图中,建立了直角坐标系xOy,按要求解答下列问题:
(1)写出△ABC三个顶点的坐标;
(2)画出△ABC向右平移6个单位后的图形△A1B1C1;
(3)求△ABC的面积.
18.探究题:
(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(3)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(4)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
参考答案
1.D.
2.A
3.C.
4.C
5.A.
6.B.
7.D
8.D.
9.答案为:A(B或C),A’(B’或C’) ,AA’(BB’或CC’)
10.答案为:70°;
11.答案为:6.
12.答案为:98
13.答案为:8.
14.答案为:2.
15.解:(1)∵△ABC中任意一点P(x1,y1)平移后的对应点为P′(x1+6,y1+4),
∴平移后对应点的横坐标加6,纵坐标加4,
∴△ABC先向右平移6个单位,再向上平移4个单位得到△A′B′C′
或△ABC先向上平移4个单位,再向右平移6个单位得到△A′B′C′;
(2)由(1)可知,A′(2,3),B′(1,0),C′(5,1);
(3)如图所示,S△A′B′C′=3×4﹣×1×3﹣×1×4﹣×2×3=5.5.
16.解:(1)利用图形得出:点A的坐标为:(2,8),点C的坐标为:(6,6);
故答案为:(2,8),(6,6);
(2)∵将△ABC向左平移7个单位,M为△ABC内的一点,其坐标为(a,b),
∴平移后点M的对应点M'的坐标为:(a﹣7,b).故答案为:(a﹣7,b).
17.解:(1)如图所示:A(﹣1,8),B(﹣5,3),C(0,6);
(2)如图所示:(3)△ABC的面积为:×(5+1)×5﹣×1×2﹣×3×5=6.5.
18.(1)相等,过E作AB的平行线即可;
(2)∠B+∠D+∠E=360°;
(3)∠B=∠D+∠E;(4)相等.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
