北师大版六年级数学下册——第三讲:比和比例-必备同步练习卷(含答案)
文档属性
| 名称 | 北师大版六年级数学下册——第三讲:比和比例-必备同步练习卷(含答案) | 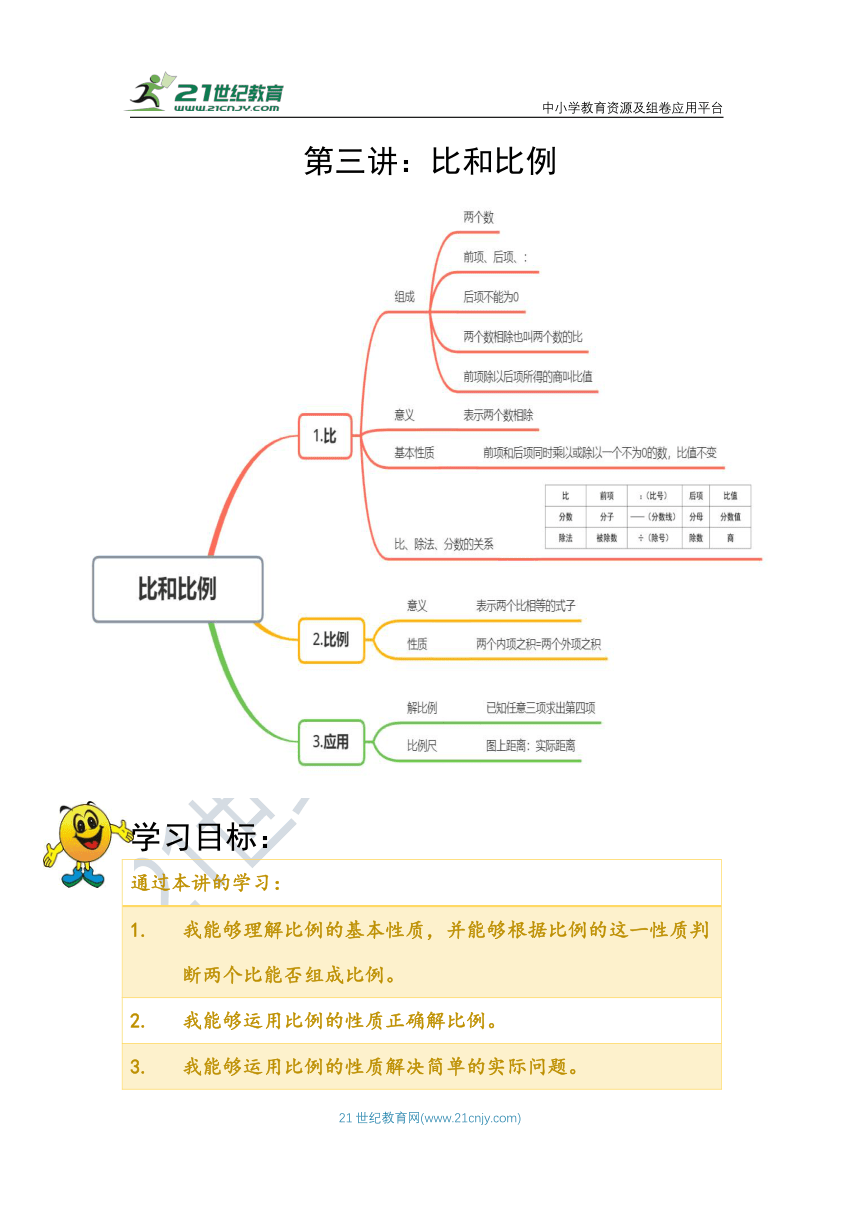 | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 13:52:46 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第三讲:比和比例
学习目标:
通过本讲的学习:
我能够理解比例的基本性质,并能够根据比例的这一性质判断两个比能否组成比例。
我能够运用比例的性质正确解比例。
我能够运用比例的性质解决简单的实际问题。
例题1
(1)写出2个比值都为0.5的比,再将它们组成比例。
(2)在24的因数中挑选4个数组成比例。
练习1
将以下四个数组成两个比例: 、
思路点拨:
化连比:(找中间量法)
例如:甲:乙=1:2,乙:丙=3:4,在解题过程中可以用份数表示各数量,两个比中都有乙,但份数不同,不能直接连比,可以先找出乙在两个比中的两个份数的最小公倍数,然后利用比的基本性质使其相等,最后改成连比。
例题2
(1)如果3a=4b,那么a:b= : 。
(2)一个比例的两个内项互为倒数,一个外项是2020,另一个外项是 。
(3)如果甲:乙=3:4,乙:丙=8:9,则甲:乙:丙= 。
练习2
(1)已知甲数的等于乙数的,甲、乙两数的比是 。
(2)比例的两个外项之积是2020,其中一个内项是,另一个内项是 。
(3)一个长方体中,长:宽=3:2,长:高=5:4,则这个长方体的长:宽:高为 。
例题3
解比例方程。
:x=:2 1.25:(+x)=5:8
练习3
x:3=:1.5 2:7=:(1.5+x)
思路点拨:
(1)数字比例尺:1:1000或者
(2)线段比例尺:
例题4
(1)两地之间的距离是600千米,画在地图上用3厘米的线段来表示,那么这幅地图的比例尺是 。
(2)在比例尺为1:20000的图纸上,量出一个操场的宽为2厘米,长为3厘米,它的实际长是多少米?宽是多少米?面积是多少平方米?
练习4
(1)两地之间的距离是20千米,画在地图上用5厘米的线段来表示,那么这幅地图的比例尺是 。
(2)A、B两地相距1200千米,在一幅比例尺为的地图上,量出A,B两地长多少?
第三讲:比和比例
学习目标:
通过本讲的学习:
我能够理解比例的基本性质,并能够根据比例的这一性质判断两个比能否组成比例。
我能够运用比例的性质正确解比例。
我能够运用比例的性质解决简单的实际问题。
例题1
(1)写出2个比值都为0.5的比,再将它们组成比例。
(2)在24的因数中挑选4个数组成比例。
(1)2:4=8:16
(2)3:6=4:8
练习1
将以下四个数组成两个比例: 、 。
24:16=
思路点拨:
化连比:(找中间量法)
例如:甲:乙=1:2,乙:丙=3:4,在解题过程中可以用份数表示各数量,两个比中都有乙,但份数不同,不能直接连比,可以先找出乙在两个比中的两个份数的最小公倍数,然后利用比的基本性质使其相等,最后改成连比。
例题2
(1)如果3a=4b,那么a:b= : 。
(2)一个比例的两个内项互为倒数,一个外项是2020,另一个外项是 。
(3)如果甲:乙=3:4,乙:丙=8:9,则甲:乙:丙= 。
(1)4:3;(2);(3)6:8:9
练习2
(1)已知甲数的等于乙数的,甲、乙两数的比是 。
(2)比例的两个外项之积是2020,其中一个内项是,另一个内项是 。
(3)一个长方体中,长:宽=3:2,长:高=5:4,则这个长方体的长:宽:高为 。
(1)9:8;(2)4040;(3)15:10:12
例题3
解比例方程。
:x=:2 1.25:(+x)=5:8
x=13.5 x=
练习3
x:3=:1.5 2:7=:(1.5+x)
x=1 x=
思路点拨:
(1)数字比例尺:1:1000或者
(2)线段比例尺:
例题4
(1)两地之间的距离是600千米,画在地图上用3厘米的线段来表示,那么这幅地图的比例尺是 。
(2)在比例尺为1:20000的图纸上,量出一个操场的宽为2厘米,长为3厘米,它的实际长是多少米?宽是多少米?面积是多少平方米?
(1)1:20000000;(2)长:600米,宽:400米,面积24万平方米
练习4
(1)两地之间的距离是20千米,画在地图上用5厘米的线段来表示,那么这幅地图的比例尺是 。
(2)A、B两地相距1200千米,在一幅比例尺为的地图上,量出A,B两地长多少?
(1)1:400000;(2)2厘米
21世纪教育网(www.21cnjy.com)
第三讲:比和比例
学习目标:
通过本讲的学习:
我能够理解比例的基本性质,并能够根据比例的这一性质判断两个比能否组成比例。
我能够运用比例的性质正确解比例。
我能够运用比例的性质解决简单的实际问题。
例题1
(1)写出2个比值都为0.5的比,再将它们组成比例。
(2)在24的因数中挑选4个数组成比例。
练习1
将以下四个数组成两个比例: 、
思路点拨:
化连比:(找中间量法)
例如:甲:乙=1:2,乙:丙=3:4,在解题过程中可以用份数表示各数量,两个比中都有乙,但份数不同,不能直接连比,可以先找出乙在两个比中的两个份数的最小公倍数,然后利用比的基本性质使其相等,最后改成连比。
例题2
(1)如果3a=4b,那么a:b= : 。
(2)一个比例的两个内项互为倒数,一个外项是2020,另一个外项是 。
(3)如果甲:乙=3:4,乙:丙=8:9,则甲:乙:丙= 。
练习2
(1)已知甲数的等于乙数的,甲、乙两数的比是 。
(2)比例的两个外项之积是2020,其中一个内项是,另一个内项是 。
(3)一个长方体中,长:宽=3:2,长:高=5:4,则这个长方体的长:宽:高为 。
例题3
解比例方程。
:x=:2 1.25:(+x)=5:8
练习3
x:3=:1.5 2:7=:(1.5+x)
思路点拨:
(1)数字比例尺:1:1000或者
(2)线段比例尺:
例题4
(1)两地之间的距离是600千米,画在地图上用3厘米的线段来表示,那么这幅地图的比例尺是 。
(2)在比例尺为1:20000的图纸上,量出一个操场的宽为2厘米,长为3厘米,它的实际长是多少米?宽是多少米?面积是多少平方米?
练习4
(1)两地之间的距离是20千米,画在地图上用5厘米的线段来表示,那么这幅地图的比例尺是 。
(2)A、B两地相距1200千米,在一幅比例尺为的地图上,量出A,B两地长多少?
第三讲:比和比例
学习目标:
通过本讲的学习:
我能够理解比例的基本性质,并能够根据比例的这一性质判断两个比能否组成比例。
我能够运用比例的性质正确解比例。
我能够运用比例的性质解决简单的实际问题。
例题1
(1)写出2个比值都为0.5的比,再将它们组成比例。
(2)在24的因数中挑选4个数组成比例。
(1)2:4=8:16
(2)3:6=4:8
练习1
将以下四个数组成两个比例: 、 。
24:16=
思路点拨:
化连比:(找中间量法)
例如:甲:乙=1:2,乙:丙=3:4,在解题过程中可以用份数表示各数量,两个比中都有乙,但份数不同,不能直接连比,可以先找出乙在两个比中的两个份数的最小公倍数,然后利用比的基本性质使其相等,最后改成连比。
例题2
(1)如果3a=4b,那么a:b= : 。
(2)一个比例的两个内项互为倒数,一个外项是2020,另一个外项是 。
(3)如果甲:乙=3:4,乙:丙=8:9,则甲:乙:丙= 。
(1)4:3;(2);(3)6:8:9
练习2
(1)已知甲数的等于乙数的,甲、乙两数的比是 。
(2)比例的两个外项之积是2020,其中一个内项是,另一个内项是 。
(3)一个长方体中,长:宽=3:2,长:高=5:4,则这个长方体的长:宽:高为 。
(1)9:8;(2)4040;(3)15:10:12
例题3
解比例方程。
:x=:2 1.25:(+x)=5:8
x=13.5 x=
练习3
x:3=:1.5 2:7=:(1.5+x)
x=1 x=
思路点拨:
(1)数字比例尺:1:1000或者
(2)线段比例尺:
例题4
(1)两地之间的距离是600千米,画在地图上用3厘米的线段来表示,那么这幅地图的比例尺是 。
(2)在比例尺为1:20000的图纸上,量出一个操场的宽为2厘米,长为3厘米,它的实际长是多少米?宽是多少米?面积是多少平方米?
(1)1:20000000;(2)长:600米,宽:400米,面积24万平方米
练习4
(1)两地之间的距离是20千米,画在地图上用5厘米的线段来表示,那么这幅地图的比例尺是 。
(2)A、B两地相距1200千米,在一幅比例尺为的地图上,量出A,B两地长多少?
(1)1:400000;(2)2厘米
21世纪教育网(www.21cnjy.com)
