北师大版六年级数学下册——第四讲:正反比例-必备同步练习卷(含答案)
文档属性
| 名称 | 北师大版六年级数学下册——第四讲:正反比例-必备同步练习卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 00:00:00 | ||
图片预览





文档简介
中小学教育资源及组卷应用平台
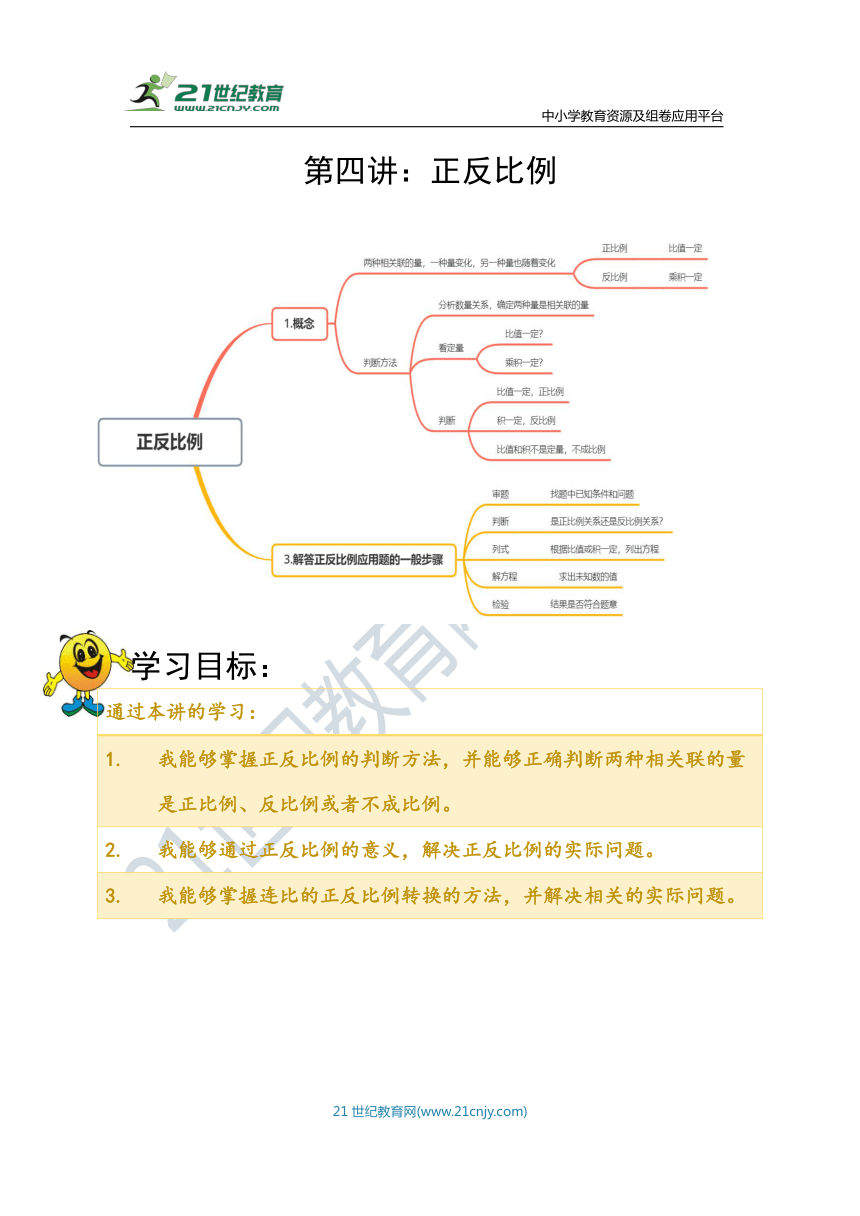
第四讲:正反比例
学习目标:
通过本讲的学习:
我能够掌握正反比例的判断方法,并能够正确判断两种相关联的量是正比例、反比例或者不成比例。
我能够通过正反比例的意义,解决正反比例的实际问题。
我能够掌握连比的正反比例转换的方法,并解决相关的实际问题。
例题1
判断:
(1)工作总量一定,工作效率和工作时间成反比例。 ( )
(2)比例尺一定,图上距离和实际距离成正比例。 ( )
(3)如果5x-7y=0(x和y均不为0),那么x和y不成比例。( )
(4)分数的大小一定(不等于0),它的分子和分母成正比例。( )
(5)在一定的距离内,车轮周长和它转动的圈数成反比例。 ( )
(6)两种相关联的量,不成正比例,就成反比例。 ( )
(7)工作总量一定,已完成的量和未完成的量成反比例。 ( )
练习1
判断:
(1)长方形的长一定,宽和面积成正比例。 ( )
(2)大米的总量一定,吃掉的和剩下的成反比例。 ( )
(3)圆的半径和周长成正比例。 ( )
(4)分数的分子一定(不等于0),分数值和分母成反比例。 ( )
(5)铺地面积一定,方砖的边长和所需块数成反比例。 ( )
(6)铺地面积一定,方砖面积和所需块数成反比例。 ( )
(7)除数一定,被除数和商成正比例。 ( )
例题2
(1)甲、乙两列火车从相距450千米的两地同时相向开出,已知甲、乙两列火车的速度比是4:5,相遇时甲火车行了 千米,乙火车行了 千米。
(2)一辆汽车从甲城开往乙城,每小时行驶68千米,5小时到达。返回时,每小时比原来慢。返回时用了多长时间?
练习2
(1)百米赛跑中,甲、乙的速度比是7:8,当乙跑完全程,甲离终点还有 米。
思路点拨:
解决用方砖铺地的问题时,应注意每块方砖的面积与所需块数成反比例关系,而不是方砖的边长与块数成反比例。
(2)陈博士家的客厅是长方形的,用边长0.9m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?
例题3
(1)A、B是两个咬合的齿轮,已知齿轮A旋转7圈时,齿轮B旋转6圈。如果A的齿数是420,那么B的齿数是多少?
(2)甲乙两地间的距离是490千米,一辆汽车5小时行驶了350千米。照这样的速度,行完全程需要几小时?
练习3
(1)大、小两个相互咬合的齿轮,它们的齿数分别是150和100,当大齿轮转动8圈时,能带动小齿轮转动几圈?
(2)甲乙两地间的距离是550千米,一辆汽车3小时行驶了330千米。照这样的速度,行完全程需要几小时?
思路点拨:
连比的正反比例转换
(1)当两种相关联的量成正比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙= a:b:c
(2)当两种相关联的量成反比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙=
例题4
甲、乙和丙三人一起去爬灵山,从山脚出发,约好在山顶见面,甲从山脚爬到山顶用了40分钟,乙和丙分别用了1小时20分钟和120分钟,则甲、乙和丙的速度比为 。
练习4
甲、乙、丙三人各自独立做同一件工程,甲用时12分钟,乙用时18分钟,丙用时20分钟,那么他们三人的工作效率比为 。
第四讲:正反比例
学习目标:
通过本讲的学习:
我能够掌握正反比例的判断方法,并能够正确判断两种相关联的量是正比例、反比例或者不成比例。
我能够通过正反比例的意义,解决正反比例的实际问题。
我能够掌握连比的正反比例转换的方法,并解决相关的实际问题。
例题1
判断:
(1)工作总量一定,工作效率和工作时间成反比例。 ( )
(2)比例尺一定,图上距离和实际距离成正比例。 ( )
(3)如果5x-7y=0(x和y均不为0),那么x和y不成比例。( )
(4)分数的大小一定(不等于0),它的分子和分母成正比例。( )
(5)在一定的距离内,车轮周长和它转动的圈数成反比例。 ( )
(6)两种相关联的量,不成正比例,就成反比例。 ( )
(7)工作总量一定,已完成的量和未完成的量成反比例。 ( )
√√×√√××
练习1
判断:
(1)长方形的长一定,宽和面积成正比例。 ( )
(2)大米的总量一定,吃掉的和剩下的成反比例。 ( )
(3)圆的半径和周长成正比例。 ( )
(4)分数的分子一定(不等于0),分数值和分母成反比例。 ( )
(5)铺地面积一定,方砖的边长和所需块数成反比例。 ( )
(6)铺地面积一定,方砖面积和所需块数成反比例。 ( )
(7)除数一定,被除数和商成正比例。 ( )
√×√√×√√
例题2
(1)甲、乙两列火车从相距450千米的两地同时相向开出,已知甲、乙两列火车的速度比是4:5,相遇时甲火车行了 千米,乙火车行了 千米。
(2)一辆汽车从甲城开往乙城,每小时行驶68千米,5小时到达。返回时,每小时比原来慢。返回时用了多长时间?
(1)200,250;(2)=17(小时)
练习2
(1)百米赛跑中,甲、乙的速度比是7:8,当乙跑完全程,甲离终点还有 米。
12.5
思路点拨:
解决用方砖铺地的问题时,应注意每块方砖的面积与所需块数成反比例关系,而不是方砖的边长与块数成反比例。
(2)陈博士家的客厅是长方形的,用边长0.9m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?
0.92×100÷0.52=324(块)
例题3
(1)A、B是两个咬合的齿轮,已知齿轮A旋转7圈时,齿轮B旋转6圈。如果A的齿数是420,那么B的齿数是多少?
420×7÷6=490
(2)甲乙两地间的距离是490千米,一辆汽车5小时行驶了350千米。照这样的速度,行完全程需要几小时?
490÷(350÷5)=7(小时)
练习3
(1)大、小两个相互咬合的齿轮,它们的齿数分别是150和100,当大齿轮转动8圈时,能带动小齿轮转动几圈?
8×150÷100=12(圈)
(2)甲乙两地间的距离是550千米,一辆汽车3小时行驶了330千米。照这样的速度,行完全程需要几小时?
550÷(330÷3)=5(小时)
思路点拨:
连比的正反比例转换
(1)当两种相关联的量成正比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙= a:b:c
(2)当两种相关联的量成反比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙=
例题4
甲、乙和丙三人一起去爬灵山,从山脚出发,约好在山顶见面,甲从山脚爬到山顶用了40分钟,乙和丙分别用了1小时20分钟和120分钟,则甲、乙和丙的速度比为 。
3:2:1
练习4
甲、乙、丙三人各自独立做同一件工程,甲用时12分钟,乙用时18分钟,丙用时20分钟,那么他们三人的工作效率比为 。
10:9:6
21世纪教育网(www.21cnjy.com)
第四讲:正反比例
学习目标:
通过本讲的学习:
我能够掌握正反比例的判断方法,并能够正确判断两种相关联的量是正比例、反比例或者不成比例。
我能够通过正反比例的意义,解决正反比例的实际问题。
我能够掌握连比的正反比例转换的方法,并解决相关的实际问题。
例题1
判断:
(1)工作总量一定,工作效率和工作时间成反比例。 ( )
(2)比例尺一定,图上距离和实际距离成正比例。 ( )
(3)如果5x-7y=0(x和y均不为0),那么x和y不成比例。( )
(4)分数的大小一定(不等于0),它的分子和分母成正比例。( )
(5)在一定的距离内,车轮周长和它转动的圈数成反比例。 ( )
(6)两种相关联的量,不成正比例,就成反比例。 ( )
(7)工作总量一定,已完成的量和未完成的量成反比例。 ( )
练习1
判断:
(1)长方形的长一定,宽和面积成正比例。 ( )
(2)大米的总量一定,吃掉的和剩下的成反比例。 ( )
(3)圆的半径和周长成正比例。 ( )
(4)分数的分子一定(不等于0),分数值和分母成反比例。 ( )
(5)铺地面积一定,方砖的边长和所需块数成反比例。 ( )
(6)铺地面积一定,方砖面积和所需块数成反比例。 ( )
(7)除数一定,被除数和商成正比例。 ( )
例题2
(1)甲、乙两列火车从相距450千米的两地同时相向开出,已知甲、乙两列火车的速度比是4:5,相遇时甲火车行了 千米,乙火车行了 千米。
(2)一辆汽车从甲城开往乙城,每小时行驶68千米,5小时到达。返回时,每小时比原来慢。返回时用了多长时间?
练习2
(1)百米赛跑中,甲、乙的速度比是7:8,当乙跑完全程,甲离终点还有 米。
思路点拨:
解决用方砖铺地的问题时,应注意每块方砖的面积与所需块数成反比例关系,而不是方砖的边长与块数成反比例。
(2)陈博士家的客厅是长方形的,用边长0.9m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?
例题3
(1)A、B是两个咬合的齿轮,已知齿轮A旋转7圈时,齿轮B旋转6圈。如果A的齿数是420,那么B的齿数是多少?
(2)甲乙两地间的距离是490千米,一辆汽车5小时行驶了350千米。照这样的速度,行完全程需要几小时?
练习3
(1)大、小两个相互咬合的齿轮,它们的齿数分别是150和100,当大齿轮转动8圈时,能带动小齿轮转动几圈?
(2)甲乙两地间的距离是550千米,一辆汽车3小时行驶了330千米。照这样的速度,行完全程需要几小时?
思路点拨:
连比的正反比例转换
(1)当两种相关联的量成正比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙= a:b:c
(2)当两种相关联的量成反比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙=
例题4
甲、乙和丙三人一起去爬灵山,从山脚出发,约好在山顶见面,甲从山脚爬到山顶用了40分钟,乙和丙分别用了1小时20分钟和120分钟,则甲、乙和丙的速度比为 。
练习4
甲、乙、丙三人各自独立做同一件工程,甲用时12分钟,乙用时18分钟,丙用时20分钟,那么他们三人的工作效率比为 。
第四讲:正反比例
学习目标:
通过本讲的学习:
我能够掌握正反比例的判断方法,并能够正确判断两种相关联的量是正比例、反比例或者不成比例。
我能够通过正反比例的意义,解决正反比例的实际问题。
我能够掌握连比的正反比例转换的方法,并解决相关的实际问题。
例题1
判断:
(1)工作总量一定,工作效率和工作时间成反比例。 ( )
(2)比例尺一定,图上距离和实际距离成正比例。 ( )
(3)如果5x-7y=0(x和y均不为0),那么x和y不成比例。( )
(4)分数的大小一定(不等于0),它的分子和分母成正比例。( )
(5)在一定的距离内,车轮周长和它转动的圈数成反比例。 ( )
(6)两种相关联的量,不成正比例,就成反比例。 ( )
(7)工作总量一定,已完成的量和未完成的量成反比例。 ( )
√√×√√××
练习1
判断:
(1)长方形的长一定,宽和面积成正比例。 ( )
(2)大米的总量一定,吃掉的和剩下的成反比例。 ( )
(3)圆的半径和周长成正比例。 ( )
(4)分数的分子一定(不等于0),分数值和分母成反比例。 ( )
(5)铺地面积一定,方砖的边长和所需块数成反比例。 ( )
(6)铺地面积一定,方砖面积和所需块数成反比例。 ( )
(7)除数一定,被除数和商成正比例。 ( )
√×√√×√√
例题2
(1)甲、乙两列火车从相距450千米的两地同时相向开出,已知甲、乙两列火车的速度比是4:5,相遇时甲火车行了 千米,乙火车行了 千米。
(2)一辆汽车从甲城开往乙城,每小时行驶68千米,5小时到达。返回时,每小时比原来慢。返回时用了多长时间?
(1)200,250;(2)=17(小时)
练习2
(1)百米赛跑中,甲、乙的速度比是7:8,当乙跑完全程,甲离终点还有 米。
12.5
思路点拨:
解决用方砖铺地的问题时,应注意每块方砖的面积与所需块数成反比例关系,而不是方砖的边长与块数成反比例。
(2)陈博士家的客厅是长方形的,用边长0.9m的方砖铺地,正好需要100块。如果改用边长0.5m的方砖铺地,需要多少块?
0.92×100÷0.52=324(块)
例题3
(1)A、B是两个咬合的齿轮,已知齿轮A旋转7圈时,齿轮B旋转6圈。如果A的齿数是420,那么B的齿数是多少?
420×7÷6=490
(2)甲乙两地间的距离是490千米,一辆汽车5小时行驶了350千米。照这样的速度,行完全程需要几小时?
490÷(350÷5)=7(小时)
练习3
(1)大、小两个相互咬合的齿轮,它们的齿数分别是150和100,当大齿轮转动8圈时,能带动小齿轮转动几圈?
8×150÷100=12(圈)
(2)甲乙两地间的距离是550千米,一辆汽车3小时行驶了330千米。照这样的速度,行完全程需要几小时?
550÷(330÷3)=5(小时)
思路点拨:
连比的正反比例转换
(1)当两种相关联的量成正比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙= a:b:c
(2)当两种相关联的量成反比例时,如果第一种量
甲:乙:丙=a:b:c,那么另一种量甲:乙:丙=
例题4
甲、乙和丙三人一起去爬灵山,从山脚出发,约好在山顶见面,甲从山脚爬到山顶用了40分钟,乙和丙分别用了1小时20分钟和120分钟,则甲、乙和丙的速度比为 。
3:2:1
练习4
甲、乙、丙三人各自独立做同一件工程,甲用时12分钟,乙用时18分钟,丙用时20分钟,那么他们三人的工作效率比为 。
10:9:6
21世纪教育网(www.21cnjy.com)
