北师大版五年级数学下册——第四讲:长方体的表面积(二)-必备同步练习卷(含答案)
文档属性
| 名称 | 北师大版五年级数学下册——第四讲:长方体的表面积(二)-必备同步练习卷(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-09 15:18:00 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
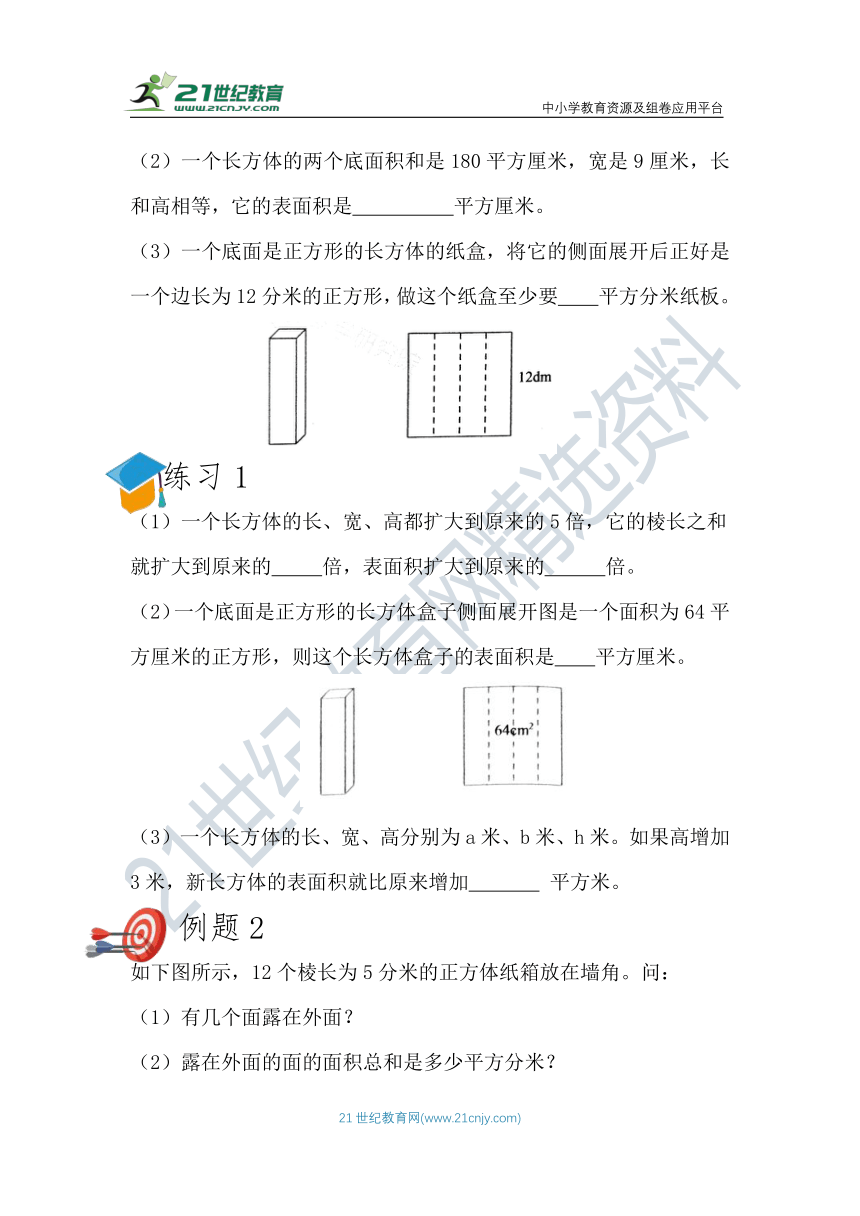
第四讲:长方体的表面积(二)
学习目标:
通过本讲的学习:
我能够理解棱长变化与棱长和、表面积变化之间的关系。
我能够利用三视图来灵活计算立体图形的表面积。
我能够熟练利用“一刀两面八棱”来灵活解决切拼类问题。
例题1
(1)一个正方体的棱长扩大到原来的6倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。
(2)一个长方体的两个底面积和是180平方厘米,宽是9厘米,长和高相等,它的表面积是 平方厘米。
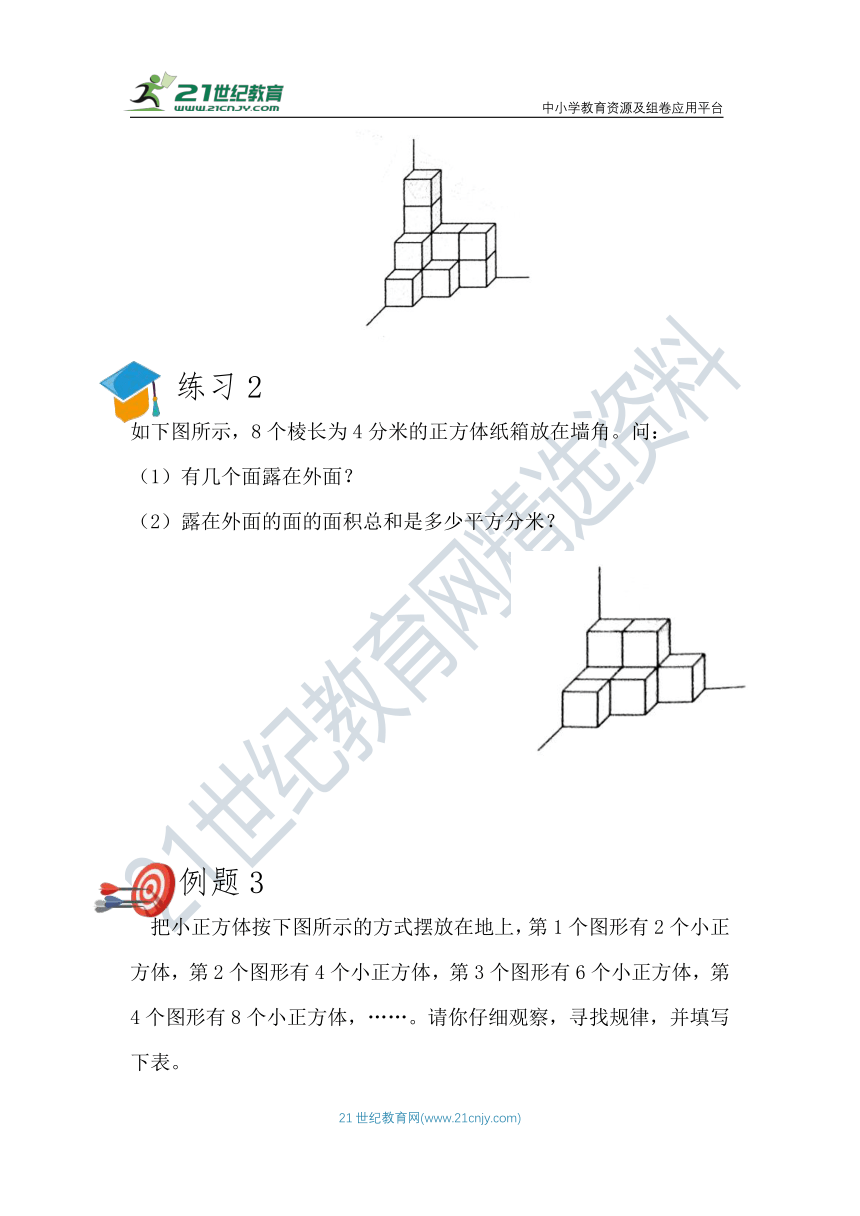
(3)一个底面是正方形的长方体的纸盒,将它的侧面展开后正好是一个边长为12分米的正方形,做这个纸盒至少要 平方分米纸板。
练习1
(1)一个长方体的长、宽、高都扩大到原来的5倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。
(2)一个底面是正方形的长方体盒子侧面展开图是一个面积为64平方厘米的正方形,则这个长方体盒子的表面积是 平方厘米。
(3)一个长方体的长、宽、高分别为a米、b米、h米。如果高增加3米,新长方体的表面积就比原来增加 平方米。
例题2
如下图所示,12个棱长为5分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
练习2
如下图所示,8个棱长为4分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
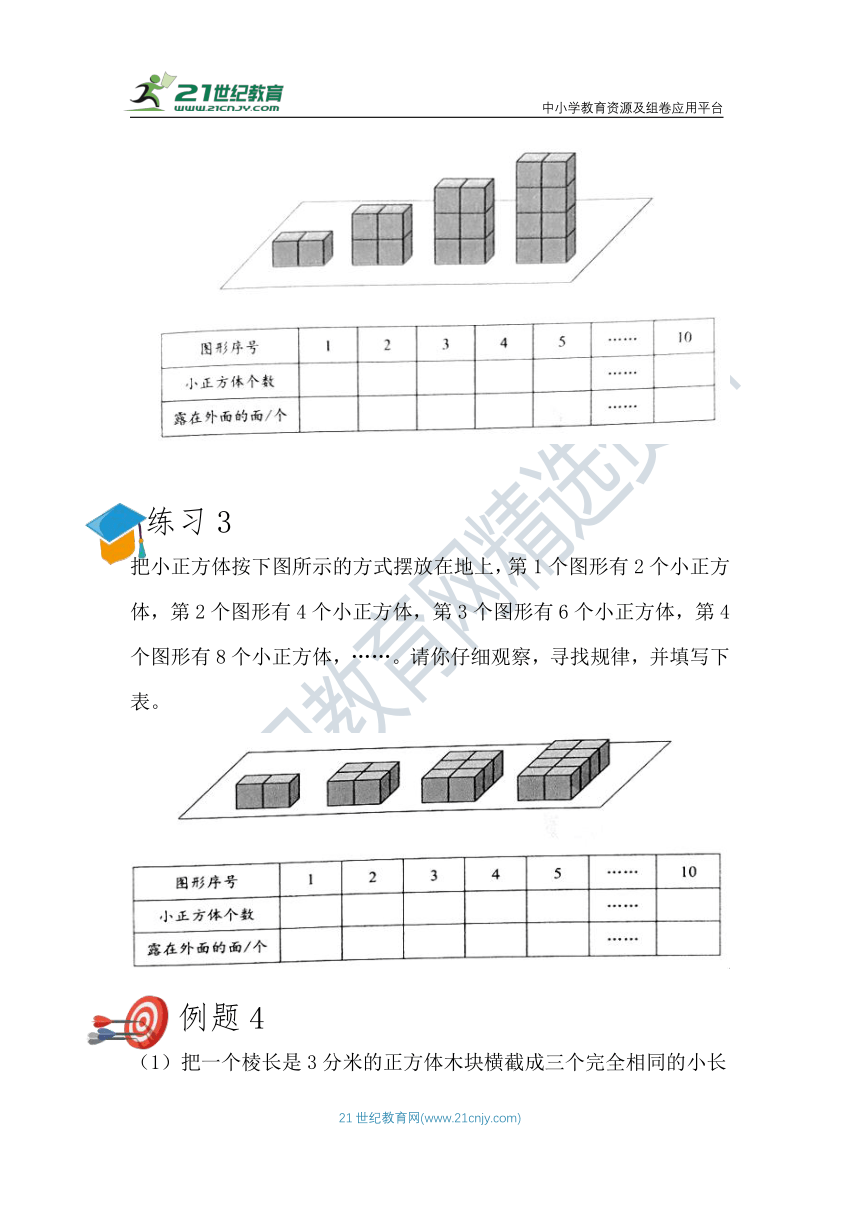
例题3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
练习3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
例题4
(1)把一个棱长是3分米的正方体木块横截成三个完全相同的小长方体后,表面积增加了 平方分米,每个小长方体的表面积是 平方分米。
(2)将4个棱长是2厘米的小正方体顺次连接成一个长方体,长方体的表面积比4个小正方体的表面积之和少了 平方厘米,这个长方体的表面积是 平方厘米。
练习4
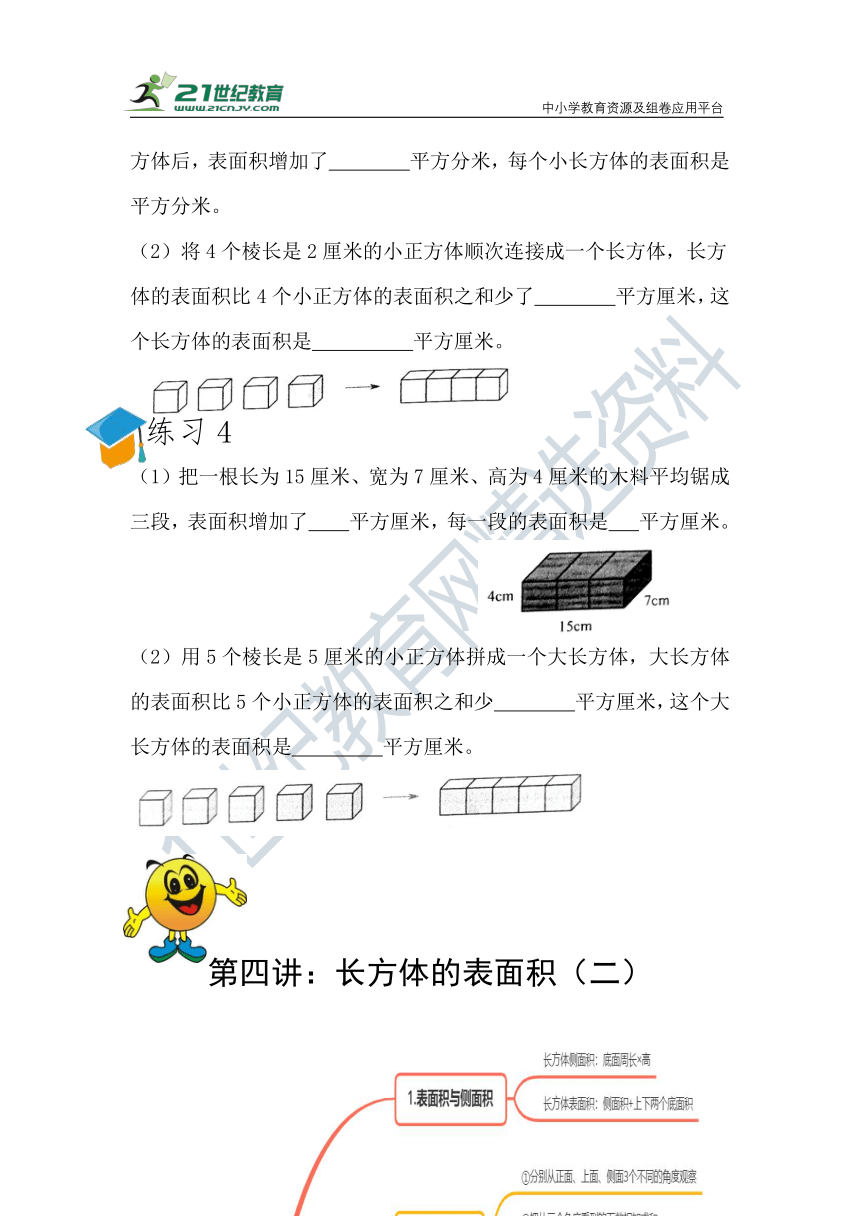
(1)把一根长为15厘米、宽为7厘米、高为4厘米的木料平均锯成三段,表面积增加了 平方厘米,每一段的表面积是 平方厘米。
(2)用5个棱长是5厘米的小正方体拼成一个大长方体,大长方体的表面积比5个小正方体的表面积之和少 平方厘米,这个大长方体的表面积是 平方厘米。
第四讲:长方体的表面积(二)
学习目标:
通过本讲的学习:
我能够理解棱长变化与棱长和、表面积变化之间的关系。
我能够利用三视图来灵活计算立体图形的表面积。
我能够熟练利用“一刀两面八棱”来灵活解决切拼类问题。
例题1
(1)一个正方体的棱长扩大到原来的6倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。6,36
(2)一个长方体的两个底面积和是180平方厘米,宽是9厘米,长和高相等,它的表面积是 平方厘米。560
(3)一个底面是正方形的长方体的纸盒,将它的侧面展开后正好是一个边长为12分米的正方形,做这个纸盒至少要 平方分米纸板。
162
练习1
(1)一个长方体的长、宽、高都扩大到原来的5倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。5,25
(2)一个底面是正方形的长方体盒子侧面展开图是一个面积为64平方厘米的正方形,则这个长方体盒子的表面积是 平方厘米。
72
(3)一个长方体的长、宽、高分别为a米、b米、h米。如果高增加3米,新长方体的表面积就比原来增加 平方米。6a+6b
例题2
如下图所示,12个棱长为5分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
21,5×5×21=525(平方分米)
练习2
如下图所示,8个棱长为4分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
15,4×4×15=240(平方分米)
例题3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
练习3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
例题4
(1)把一个棱长是3分米的正方体木块横截成三个完全相同的小长方体后,表面积增加了 平方分米,每个小长方体的表面积是 平方分米。36,30
(2)将4个棱长是2厘米的小正方体顺次连接成一个长方体,长方体的表面积比4个小正方体的表面积之和少了 平方厘米,这个长方体的表面积是 平方厘米。
24,72
练习4
(1)把一根长为15厘米、宽为7厘米、高为4厘米的木料平均锯成三段,表面积增加了 平方厘米,每一段的表面积是 平方厘米。
112,166
(2)用5个棱长是5厘米的小正方体拼成一个大长方体,大长方体的表面积比5个小正方体的表面积之和少 平方厘米,这个大长方体的表面积是 平方厘米。
200,550
21世纪教育网(www.21cnjy.com)
第四讲:长方体的表面积(二)
学习目标:
通过本讲的学习:
我能够理解棱长变化与棱长和、表面积变化之间的关系。
我能够利用三视图来灵活计算立体图形的表面积。
我能够熟练利用“一刀两面八棱”来灵活解决切拼类问题。
例题1
(1)一个正方体的棱长扩大到原来的6倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。
(2)一个长方体的两个底面积和是180平方厘米,宽是9厘米,长和高相等,它的表面积是 平方厘米。
(3)一个底面是正方形的长方体的纸盒,将它的侧面展开后正好是一个边长为12分米的正方形,做这个纸盒至少要 平方分米纸板。
练习1
(1)一个长方体的长、宽、高都扩大到原来的5倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。
(2)一个底面是正方形的长方体盒子侧面展开图是一个面积为64平方厘米的正方形,则这个长方体盒子的表面积是 平方厘米。
(3)一个长方体的长、宽、高分别为a米、b米、h米。如果高增加3米,新长方体的表面积就比原来增加 平方米。
例题2
如下图所示,12个棱长为5分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
练习2
如下图所示,8个棱长为4分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
例题3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
练习3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
例题4
(1)把一个棱长是3分米的正方体木块横截成三个完全相同的小长方体后,表面积增加了 平方分米,每个小长方体的表面积是 平方分米。
(2)将4个棱长是2厘米的小正方体顺次连接成一个长方体,长方体的表面积比4个小正方体的表面积之和少了 平方厘米,这个长方体的表面积是 平方厘米。
练习4
(1)把一根长为15厘米、宽为7厘米、高为4厘米的木料平均锯成三段,表面积增加了 平方厘米,每一段的表面积是 平方厘米。
(2)用5个棱长是5厘米的小正方体拼成一个大长方体,大长方体的表面积比5个小正方体的表面积之和少 平方厘米,这个大长方体的表面积是 平方厘米。
第四讲:长方体的表面积(二)
学习目标:
通过本讲的学习:
我能够理解棱长变化与棱长和、表面积变化之间的关系。
我能够利用三视图来灵活计算立体图形的表面积。
我能够熟练利用“一刀两面八棱”来灵活解决切拼类问题。
例题1
(1)一个正方体的棱长扩大到原来的6倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。6,36
(2)一个长方体的两个底面积和是180平方厘米,宽是9厘米,长和高相等,它的表面积是 平方厘米。560
(3)一个底面是正方形的长方体的纸盒,将它的侧面展开后正好是一个边长为12分米的正方形,做这个纸盒至少要 平方分米纸板。
162
练习1
(1)一个长方体的长、宽、高都扩大到原来的5倍,它的棱长之和就扩大到原来的 倍,表面积扩大到原来的 倍。5,25
(2)一个底面是正方形的长方体盒子侧面展开图是一个面积为64平方厘米的正方形,则这个长方体盒子的表面积是 平方厘米。
72
(3)一个长方体的长、宽、高分别为a米、b米、h米。如果高增加3米,新长方体的表面积就比原来增加 平方米。6a+6b
例题2
如下图所示,12个棱长为5分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
21,5×5×21=525(平方分米)
练习2
如下图所示,8个棱长为4分米的正方体纸箱放在墙角。问:
(1)有几个面露在外面?
(2)露在外面的面的面积总和是多少平方分米?
15,4×4×15=240(平方分米)
例题3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
练习3
把小正方体按下图所示的方式摆放在地上,第1个图形有2个小正方体,第2个图形有4个小正方体,第3个图形有6个小正方体,第4个图形有8个小正方体,……。请你仔细观察,寻找规律,并填写下表。
例题4
(1)把一个棱长是3分米的正方体木块横截成三个完全相同的小长方体后,表面积增加了 平方分米,每个小长方体的表面积是 平方分米。36,30
(2)将4个棱长是2厘米的小正方体顺次连接成一个长方体,长方体的表面积比4个小正方体的表面积之和少了 平方厘米,这个长方体的表面积是 平方厘米。
24,72
练习4
(1)把一根长为15厘米、宽为7厘米、高为4厘米的木料平均锯成三段,表面积增加了 平方厘米,每一段的表面积是 平方厘米。
112,166
(2)用5个棱长是5厘米的小正方体拼成一个大长方体,大长方体的表面积比5个小正方体的表面积之和少 平方厘米,这个大长方体的表面积是 平方厘米。
200,550
21世纪教育网(www.21cnjy.com)
