2021-2022学年八年级数学下册:17.2勾股定理的逆定理(2)学案 (无答案)
文档属性
| 名称 | 2021-2022学年八年级数学下册:17.2勾股定理的逆定理(2)学案 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 48.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 22:09:52 | ||
图片预览

文档简介
17.2勾股定理的逆定理(2)
课型:新授 执笔: 审核:八年级数学组 时间:
【学习目标】
1.理解勾股定理及其逆定理的区别与联系,并能解决实际问题
2.培养逻辑推理能力,体会“形”与“数”的结合。
3.在不同条件、不同环境中反复运用定理,达到熟练使用,灵活运用的程度。
【学习重点】勾股定理的逆定理
【学习难点】勾股定理的逆定理的应用
一、学前准备:
1、三角形三边之比为3:4:5,则这个三角形三边上的高的比为( )
A、3:4:5 B、5:4:3 C、20:15:12 D、10:8:2
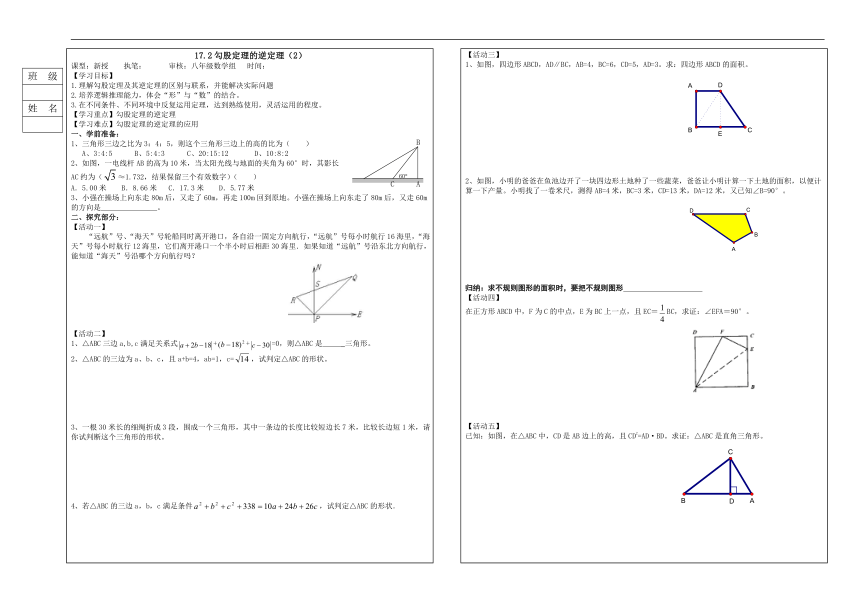
2、如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC约为(≈1.732,结果保留三个有效数字)( )
A.5.00米 B.8.66米 C.17.3米 D.5.77米
3、小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。
二、探究部分:
【活动一】
“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【活动二】
1、△ABC三边a,b,c满足关系式++=0,则△ABC是 _三角形。
2、△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状。
3、一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
4、若△ABC的三边a,b,c满足条件,试判定△ABC的形状.
【活动三】
1、如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3。求:四边形ABCD的面积。
2、如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
归纳:求不规则图形的面积时,要把不规则图形
【活动四】
在正方形ABCD中,F为C的中点,E为BC上一点,且EC=BC,求证:∠EFA=90°。
【活动五】
已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD。求证:△ABC是直角三角形。
【活动六】
已知:如图,∠DAC=∠EAC,AD=AE,D为BC上一点,且BD=DC,AC2=AE2+CE2。
求证:AB2=AE2+CE2。
三、学习体会:
四、课堂检测:
17.2勾股定理的逆定理(2)课堂检测:
1、若一个三角形的三边长分别为m+1,m+2,m+3,当m=_____时,此三角形是直角三角形。
2、一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1.5小时后,它们相距________海里.
3、小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为 .
4、如图四边形ABCD,AB=1,BC=,CD=,AD=3,且AB⊥BC。求:四边形ABCD的面积
5、阅读下列题目的解题过程:
已知:a、b、c为三角形ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4 (A)
∴c2 (a2-b2)=(a2+b2)(a2-b2) (B)
∴c2=a2+b2 (C)
∴△ABC为直角三角形
问:(1)上述解题过程,从哪一步开始出现错误? 请写出该步的代号_____
(2)错误的原因_________________________
(3)本题正确的结论是__________________________
(
班 级
姓 名
)
课型:新授 执笔: 审核:八年级数学组 时间:
【学习目标】
1.理解勾股定理及其逆定理的区别与联系,并能解决实际问题
2.培养逻辑推理能力,体会“形”与“数”的结合。
3.在不同条件、不同环境中反复运用定理,达到熟练使用,灵活运用的程度。
【学习重点】勾股定理的逆定理
【学习难点】勾股定理的逆定理的应用
一、学前准备:
1、三角形三边之比为3:4:5,则这个三角形三边上的高的比为( )
A、3:4:5 B、5:4:3 C、20:15:12 D、10:8:2
2、如图,一电线杆AB的高为10米,当太阳光线与地面的夹角为60°时,其影长AC约为(≈1.732,结果保留三个有效数字)( )
A.5.00米 B.8.66米 C.17.3米 D.5.77米
3、小强在操场上向东走80m后,又走了60m,再走100m回到原地。小强在操场上向东走了80m后,又走60m的方向是 。
二、探究部分:
【活动一】
“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里,它们离开港口一个半小时后相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
【活动二】
1、△ABC三边a,b,c满足关系式++=0,则△ABC是 _三角形。
2、△ABC的三边为a、b、c,且a+b=4,ab=1,c=,试判定△ABC的形状。
3、一根30米长的细绳折成3段,围成一个三角形,其中一条边的长度比较短边长7米,比较长边短1米,请你试判断这个三角形的形状。
4、若△ABC的三边a,b,c满足条件,试判定△ABC的形状.
【活动三】
1、如图,四边形ABCD,AD∥BC,AB=4,BC=6,CD=5,AD=3。求:四边形ABCD的面积。
2、如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量。小明找了一卷米尺,测得AB=4米,BC=3米,CD=13米,DA=12米,又已知∠B=90°。
归纳:求不规则图形的面积时,要把不规则图形
【活动四】
在正方形ABCD中,F为C的中点,E为BC上一点,且EC=BC,求证:∠EFA=90°。
【活动五】
已知:如图,在△ABC中,CD是AB边上的高,且CD2=AD·BD。求证:△ABC是直角三角形。
【活动六】
已知:如图,∠DAC=∠EAC,AD=AE,D为BC上一点,且BD=DC,AC2=AE2+CE2。
求证:AB2=AE2+CE2。
三、学习体会:
四、课堂检测:
17.2勾股定理的逆定理(2)课堂检测:
1、若一个三角形的三边长分别为m+1,m+2,m+3,当m=_____时,此三角形是直角三角形。
2、一轮船以16海里/时的速度从A港向东北方向航行,另一艘船同时以12海里/时的速度从A港向西北方向航行,经过1.5小时后,它们相距________海里.
3、小刚准备测量河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,河水的深度为 .
4、如图四边形ABCD,AB=1,BC=,CD=,AD=3,且AB⊥BC。求:四边形ABCD的面积
5、阅读下列题目的解题过程:
已知:a、b、c为三角形ABC的三边,且满足a2c2-b2c2=a4-b4,试判断△ABC的形状
解:∵a2c2-b2c2=a4-b4 (A)
∴c2 (a2-b2)=(a2+b2)(a2-b2) (B)
∴c2=a2+b2 (C)
∴△ABC为直角三角形
问:(1)上述解题过程,从哪一步开始出现错误? 请写出该步的代号_____
(2)错误的原因_________________________
(3)本题正确的结论是__________________________
(
班 级
姓 名
)
