4.2直线、射线、线段
图片预览




文档简介
课件29张PPT。七年级数学上册
(人教版2012年秋季使用)
几何图形初步 4.2 直线、射线、线段
(第1课时)课件说明 本课学习的是直线、射线、线段的概念、性质、表示法、画法及计算,这些内容是几何学习的重要基础,也是后续图形学习不可或缺的前提条件.学习目标:
1. 探究得到“两点确定一条直线”的事实,并能举例说明这一事实;
2. 理解直线、射线、线段的概念并掌握其表示法,认识他们之间的练习与区别;
3. 能读懂简单的几何语言并据此作出图形.课件说明学习重点:
直线、射线、线段的概念及其表示法.
使用本课件需注意:
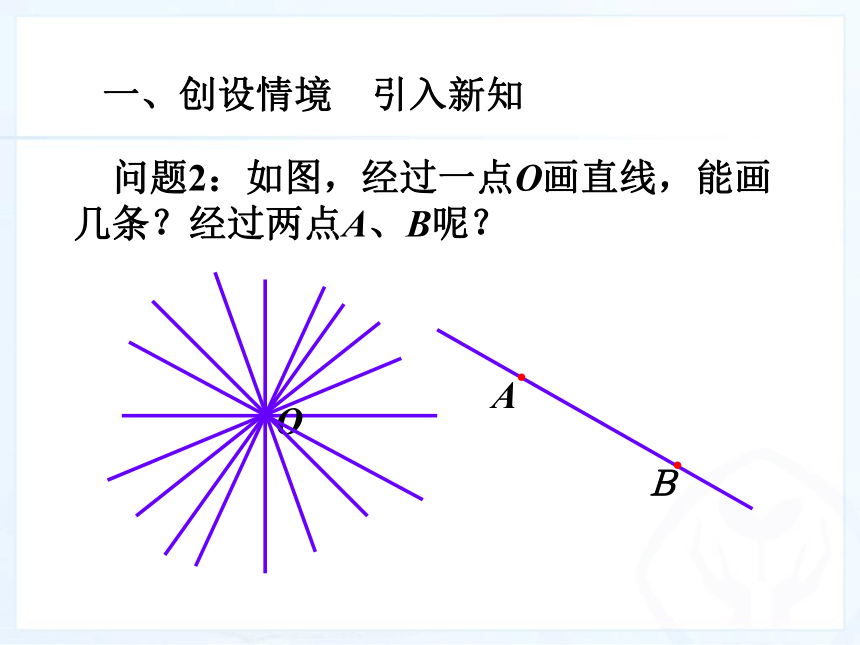
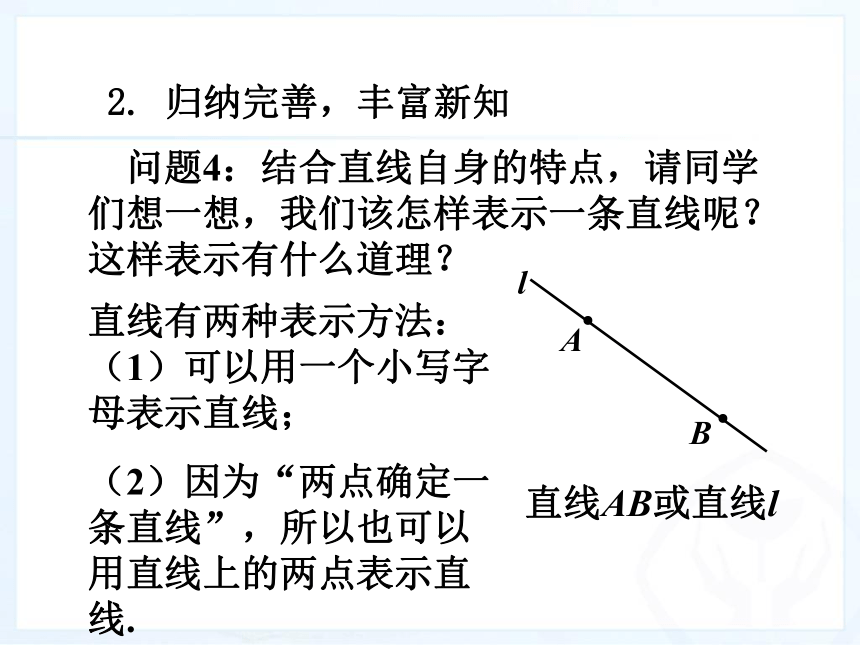
本课是实际意义上的几何起始课.学生在之前的学习中对几何图形的认识更多的停留在形象化的“感性认识”,而中学学段的几何学习更重视严谨的“逻辑论证”.所以教学中应注意课件演示的一些内容应督促学生落笔,不要仅仅停留在观看.1. 以旧悟新,探求新知 问题1:小学的时候我们已经学习过直线、射线和线段,请同学们回忆一下他们的形状并分别画出一条直线、射线和线段.·O 问题2:如图,经过一点O画直线,能画几条?经过两点A、B呢?一、创设情境 引入新知 问题3:你还能举出一些实际生活中应用“两点确定一条直线”的实例吗?一、创设情境 引入新知 问题4:结合直线自身的特点,请同学们想一想,我们该怎样表示一条直线呢?这样表示有什么道理?2. 归纳完善,丰富新知直线有两种表示方法:(1)可以用一个小写字母表示直线;
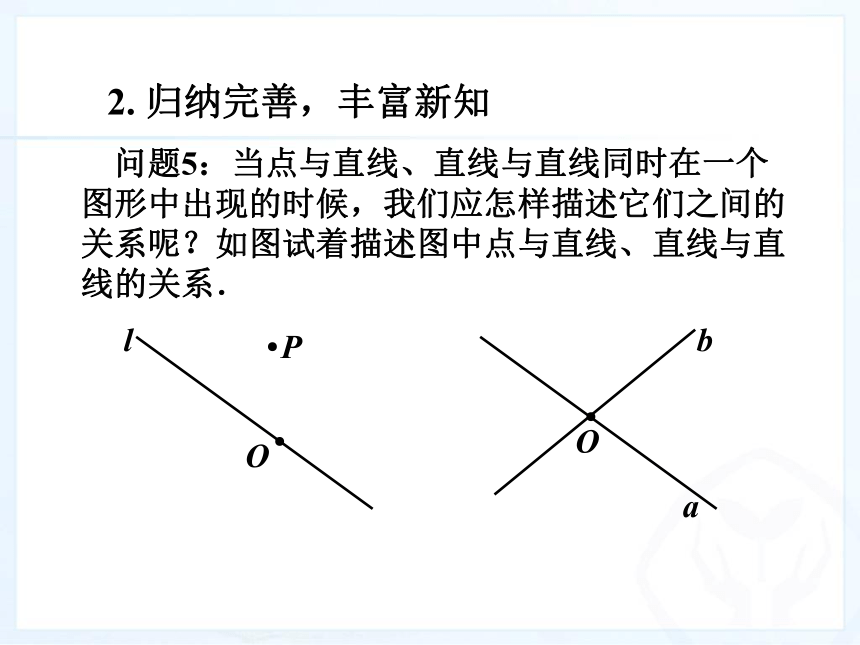
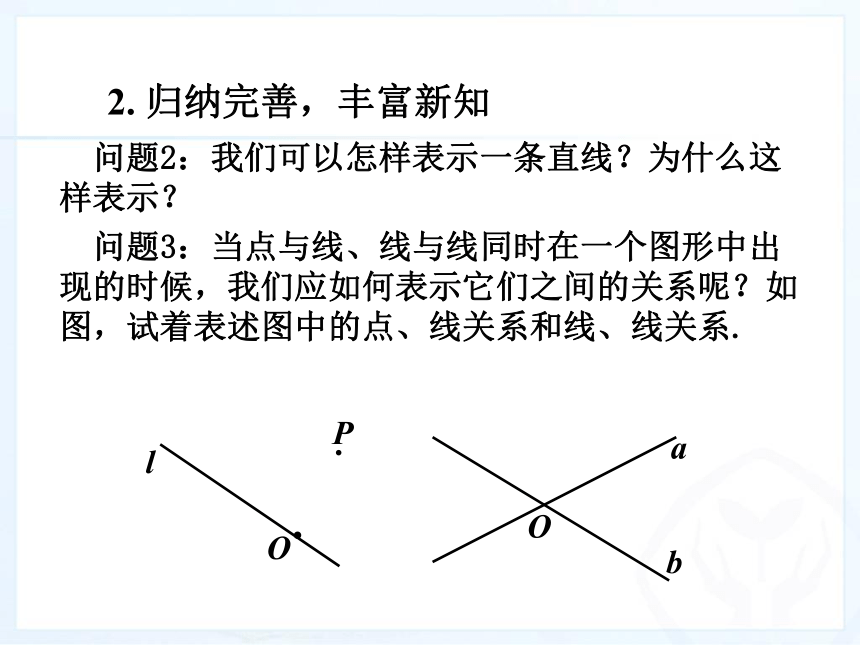
(2)因为“两点确定一条直线”,所以也可以用直线上的两点表示直线. ●●ABl直线AB或直线l 问题5:当点与直线、直线与直线同时在一个图形中出现的时候,我们应怎样描述它们之间的关系呢?如图试着描述图中点与直线、直线与直线的关系.2. 归纳完善,丰富新知 问题2:我们可以怎样表示一条直线?为什么这样表示? 2. 归纳完善,丰富新知 归纳:
(1)点与直线的位置关系:
点在直线上(直线经过点);
点不在直线上(直线不经过点).
(2)当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点.2. 归纳完善,丰富新知 问题6:
(1)用恰当的语句描述图中点与直线,直线与直线的关系. 3. 即时练习,巩固新知 (2)按下列语句画出图形:
①直线EF经过点C;
②点A在直线 l 外;
③直线AB与直线CD相交于点A.3. 即时练习,巩固新知 问题7:射线和线段都是直线的一部分,类比直线的表示方法,你认为应怎样恰当的表示射线和线段呢?请你举出一些生活中能看成射线、线段的实例. 4. 合作交流,再获新知 问题8:
(1)已知线段AB,你能由线段AB得到直线AB和射线AB吗?
(2)能否用几何语言简单描述一下直线、射线、线段? 问题9:填写表格,归纳直线、射线、线段的联系与区别.4. 合作交流,再获新知 问题10:
(1)判断下列说法是否正确:
①线段AB与射线AB都是直线AB的一部分;
②直线AB与直线BA是同一条直线;
③射线AB和射线BA是同一条射线;
④把线段向一个方向无限延伸可得到射线,把线段向两个方向无限延伸可得到直线.
4. 合作交流,再获新知 问题10:(2)按下列语句画出图形:
①点A在线段MN上; ③经过O点的三条线段a,b,c;
②射线AB不经过点P;④线段AB、CD相交于点B.4. 合作交流,再获新知 问题11:通过本节课的学习,你知道了什么?学会了什么?领悟了什么?5.课堂小结,自我完善 作业:教科书习题4.2第1,2,3,4题. 七年级数学上册
(人教版2012年秋季使用)
几何图形初步 4.2 直线、射线、线段
(第2课时)课件说明 本课学习的是与“直线、射线、线段”有关的图形的画法,在图形与几何的教学中,图形的画法是一项重要内容,学生对画图的体会是后续进行“说理论证”的重要基础.本课要求学生能够画出一条线段等于已知线段,并通过观察、思考探究等活动归纳出“两点之间线段最短”这一基本事实.课件说明学习目标:
1. 理解“两点确定一条直线”的基本事实,掌握直线、射线、线段的表示方法,理解直线、射线、线段的联系与区别;
2. 能够理解“经过” 、“确定”等几何语言的意义,并能根据几何语言画出简单的图形;
3. 激发学习兴趣,培养应用意识.
学习重点:
直线、射线、线段的表示方法及它们之间的区别.
在本课的教学中一定要注意课件演示和教师的演示作图相结合,使学生对“使用圆规截取线段等于已知线段”等基本操作有一个直观的认识.
一、开门见山,引入新知 问题1:老师手里的纸上有一条线段,你能在你的本上作出一条同样大小的线段来吗? a二、概念延伸,思维提升 问题2:黑板上有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
1.度量法
2.叠合法(叠合法要注意什么问题?)
练习1:判断线段AB和CD的大小.
(1)如图1,线段AB和CD的大小关系是AB CD;
(2)如图2,线段AB和CD的大小关系是AB CD;
(3)如图3,线段AB和CD的大小关系是AB CD. 二、概念延伸,思维提升 问题3: 如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗?(1) AB<AC(2) AC-AB=BC
AC-BC=AB
BC+AB=AC
二、概念延伸,思维提升 问题4: 如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?BCBCAC=a+bCB=a-b二、概念延伸,思维提升 问题5:如图,已知线段a,求作线段AB=2a. 那么什么叫做三等分点?四等分点呢?二、概念延伸,思维提升三、练习巩固,深化新知四、猜想验证,拓展新知问题6: 如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线. 1. 两点的所有连线中,线段最短. 简单地说:两点之间,线段最短. 2. 连接两点间的线段的长度,叫做这两点的距离.(五)课堂小结,布置作业 问题7: 这节课你学到了什么?作业:教科书习题4.2第5~8题.
(人教版2012年秋季使用)
几何图形初步 4.2 直线、射线、线段
(第1课时)课件说明 本课学习的是直线、射线、线段的概念、性质、表示法、画法及计算,这些内容是几何学习的重要基础,也是后续图形学习不可或缺的前提条件.学习目标:
1. 探究得到“两点确定一条直线”的事实,并能举例说明这一事实;
2. 理解直线、射线、线段的概念并掌握其表示法,认识他们之间的练习与区别;
3. 能读懂简单的几何语言并据此作出图形.课件说明学习重点:
直线、射线、线段的概念及其表示法.
使用本课件需注意:
本课是实际意义上的几何起始课.学生在之前的学习中对几何图形的认识更多的停留在形象化的“感性认识”,而中学学段的几何学习更重视严谨的“逻辑论证”.所以教学中应注意课件演示的一些内容应督促学生落笔,不要仅仅停留在观看.1. 以旧悟新,探求新知 问题1:小学的时候我们已经学习过直线、射线和线段,请同学们回忆一下他们的形状并分别画出一条直线、射线和线段.·O 问题2:如图,经过一点O画直线,能画几条?经过两点A、B呢?一、创设情境 引入新知 问题3:你还能举出一些实际生活中应用“两点确定一条直线”的实例吗?一、创设情境 引入新知 问题4:结合直线自身的特点,请同学们想一想,我们该怎样表示一条直线呢?这样表示有什么道理?2. 归纳完善,丰富新知直线有两种表示方法:(1)可以用一个小写字母表示直线;
(2)因为“两点确定一条直线”,所以也可以用直线上的两点表示直线. ●●ABl直线AB或直线l 问题5:当点与直线、直线与直线同时在一个图形中出现的时候,我们应怎样描述它们之间的关系呢?如图试着描述图中点与直线、直线与直线的关系.2. 归纳完善,丰富新知 问题2:我们可以怎样表示一条直线?为什么这样表示? 2. 归纳完善,丰富新知 归纳:
(1)点与直线的位置关系:
点在直线上(直线经过点);
点不在直线上(直线不经过点).
(2)当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做他们的交点.2. 归纳完善,丰富新知 问题6:
(1)用恰当的语句描述图中点与直线,直线与直线的关系. 3. 即时练习,巩固新知 (2)按下列语句画出图形:
①直线EF经过点C;
②点A在直线 l 外;
③直线AB与直线CD相交于点A.3. 即时练习,巩固新知 问题7:射线和线段都是直线的一部分,类比直线的表示方法,你认为应怎样恰当的表示射线和线段呢?请你举出一些生活中能看成射线、线段的实例. 4. 合作交流,再获新知 问题8:
(1)已知线段AB,你能由线段AB得到直线AB和射线AB吗?
(2)能否用几何语言简单描述一下直线、射线、线段? 问题9:填写表格,归纳直线、射线、线段的联系与区别.4. 合作交流,再获新知 问题10:
(1)判断下列说法是否正确:
①线段AB与射线AB都是直线AB的一部分;
②直线AB与直线BA是同一条直线;
③射线AB和射线BA是同一条射线;
④把线段向一个方向无限延伸可得到射线,把线段向两个方向无限延伸可得到直线.
4. 合作交流,再获新知 问题10:(2)按下列语句画出图形:
①点A在线段MN上; ③经过O点的三条线段a,b,c;
②射线AB不经过点P;④线段AB、CD相交于点B.4. 合作交流,再获新知 问题11:通过本节课的学习,你知道了什么?学会了什么?领悟了什么?5.课堂小结,自我完善 作业:教科书习题4.2第1,2,3,4题. 七年级数学上册
(人教版2012年秋季使用)
几何图形初步 4.2 直线、射线、线段
(第2课时)课件说明 本课学习的是与“直线、射线、线段”有关的图形的画法,在图形与几何的教学中,图形的画法是一项重要内容,学生对画图的体会是后续进行“说理论证”的重要基础.本课要求学生能够画出一条线段等于已知线段,并通过观察、思考探究等活动归纳出“两点之间线段最短”这一基本事实.课件说明学习目标:
1. 理解“两点确定一条直线”的基本事实,掌握直线、射线、线段的表示方法,理解直线、射线、线段的联系与区别;
2. 能够理解“经过” 、“确定”等几何语言的意义,并能根据几何语言画出简单的图形;
3. 激发学习兴趣,培养应用意识.
学习重点:
直线、射线、线段的表示方法及它们之间的区别.
在本课的教学中一定要注意课件演示和教师的演示作图相结合,使学生对“使用圆规截取线段等于已知线段”等基本操作有一个直观的认识.
一、开门见山,引入新知 问题1:老师手里的纸上有一条线段,你能在你的本上作出一条同样大小的线段来吗? a二、概念延伸,思维提升 问题2:黑板上有两条线段,你能判断一下它们的长短吗?你有什么方法来验证你的判断?
1.度量法
2.叠合法(叠合法要注意什么问题?)
练习1:判断线段AB和CD的大小.
(1)如图1,线段AB和CD的大小关系是AB CD;
(2)如图2,线段AB和CD的大小关系是AB CD;
(3)如图3,线段AB和CD的大小关系是AB CD. 二、概念延伸,思维提升 问题3: 如图,线段AB和AC的大小关系是怎样的?线段AC与线段AB的差是哪条线段?你还能从图中观察出其他线段间的和、差关系吗?(1) AB<AC(2) AC-AB=BC
AC-BC=AB
BC+AB=AC
二、概念延伸,思维提升 问题4: 如图,已知线段a和线段b,怎样通过作图得到a与b的和、a与b的差呢?BCBCAC=a+bCB=a-b二、概念延伸,思维提升 问题5:如图,已知线段a,求作线段AB=2a. 那么什么叫做三等分点?四等分点呢?二、概念延伸,思维提升三、练习巩固,深化新知四、猜想验证,拓展新知问题6: 如图,从A地到B地有四条道路,除它们之外能否再修一条从A地到B地的最短道路?如果能,请联系你以前所学的知识,在图上画出最短路线. 1. 两点的所有连线中,线段最短. 简单地说:两点之间,线段最短. 2. 连接两点间的线段的长度,叫做这两点的距离.(五)课堂小结,布置作业 问题7: 这节课你学到了什么?作业:教科书习题4.2第5~8题.
