2021-2022学年北师大版九年级数学下册3.3垂径定理同步达标训练(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册3.3垂径定理同步达标训练(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 369.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 17:17:17 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《3.3垂径定理》同步达标训练(附答案)
1.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
2.如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
A.4 B.6 C.2 D.8
3.如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A.6 B.12 C.15 D.30
4.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
5.如图,已知⊙O的直径AB⊥CD于点E,则下列结论不一定成立的是( )
A.CE=DE B.AE=OE C.= D.△OCE≌△ODE
6.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.cm B.cm C.cm或cm D.cm或cm
7.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A.3 B.3 C. D.
8.在⊙O内有一点P,已知OP=,且圆内过点P的最短弦长为6,则⊙O的面积是( )
A.6π B.8π C.10π D.12π
9.在△ABC中,AB=AC=5,sinB=,⊙O过点B、C两点,且⊙O半径r=,则OA的长为( )
A.3或5 B.5 C.4或5 D.4
10.如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 .
11.如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
12.如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
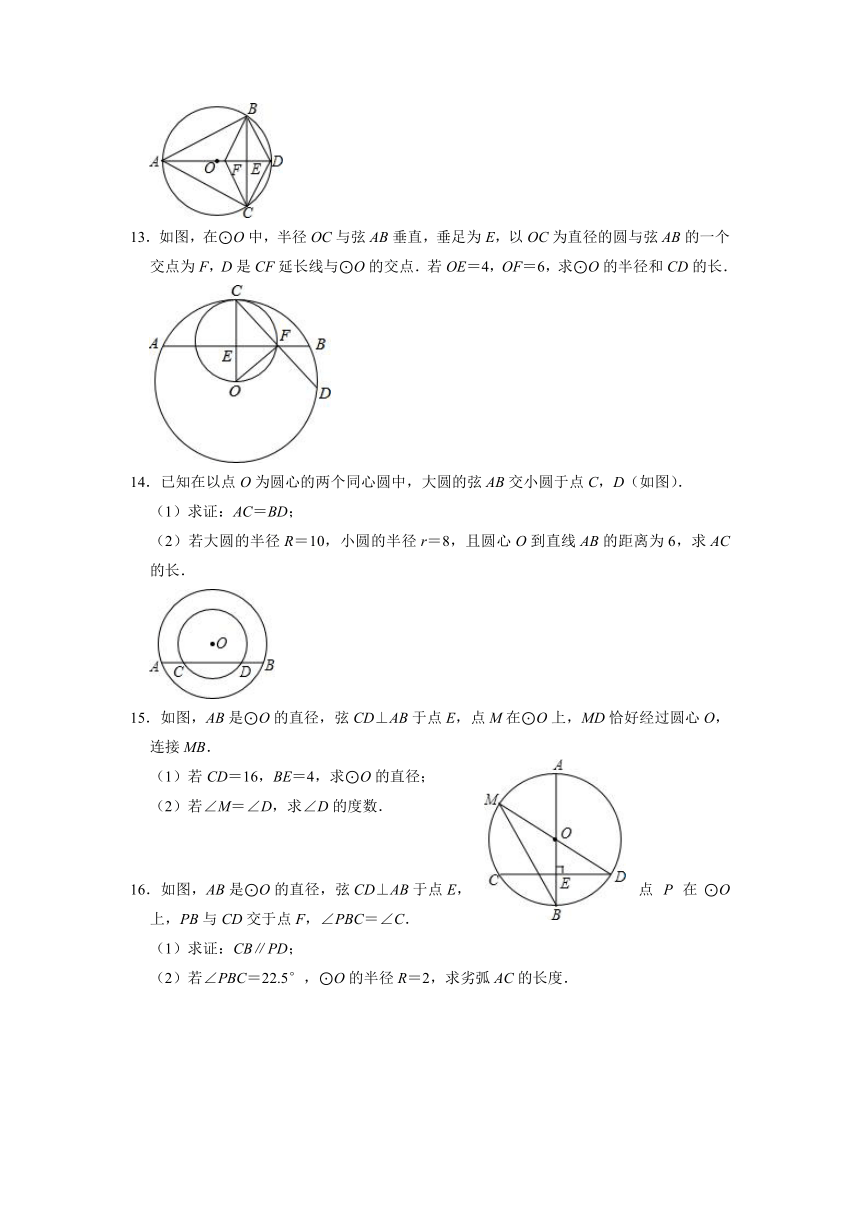
13.如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.
14.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
15.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
16.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
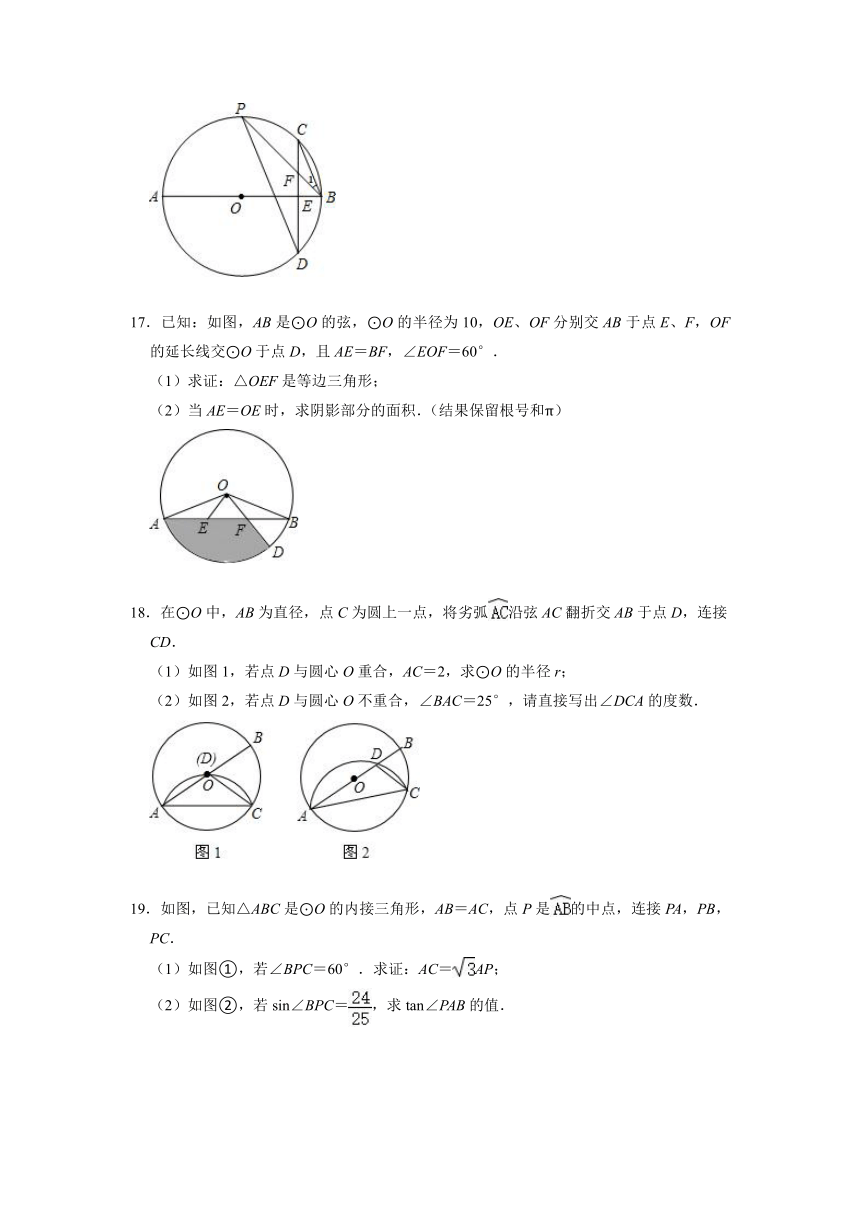
17.已知:如图,AB是⊙O的弦,⊙O的半径为10,OE、OF分别交AB于点E、F,OF的延长线交⊙O于点D,且AE=BF,∠EOF=60°.
(1)求证:△OEF是等边三角形;
(2)当AE=OE时,求阴影部分的面积.(结果保留根号和π)
18.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
19.如图,已知△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°.求证:AC=AP;
(2)如图②,若sin∠BPC=,求tan∠PAB的值.
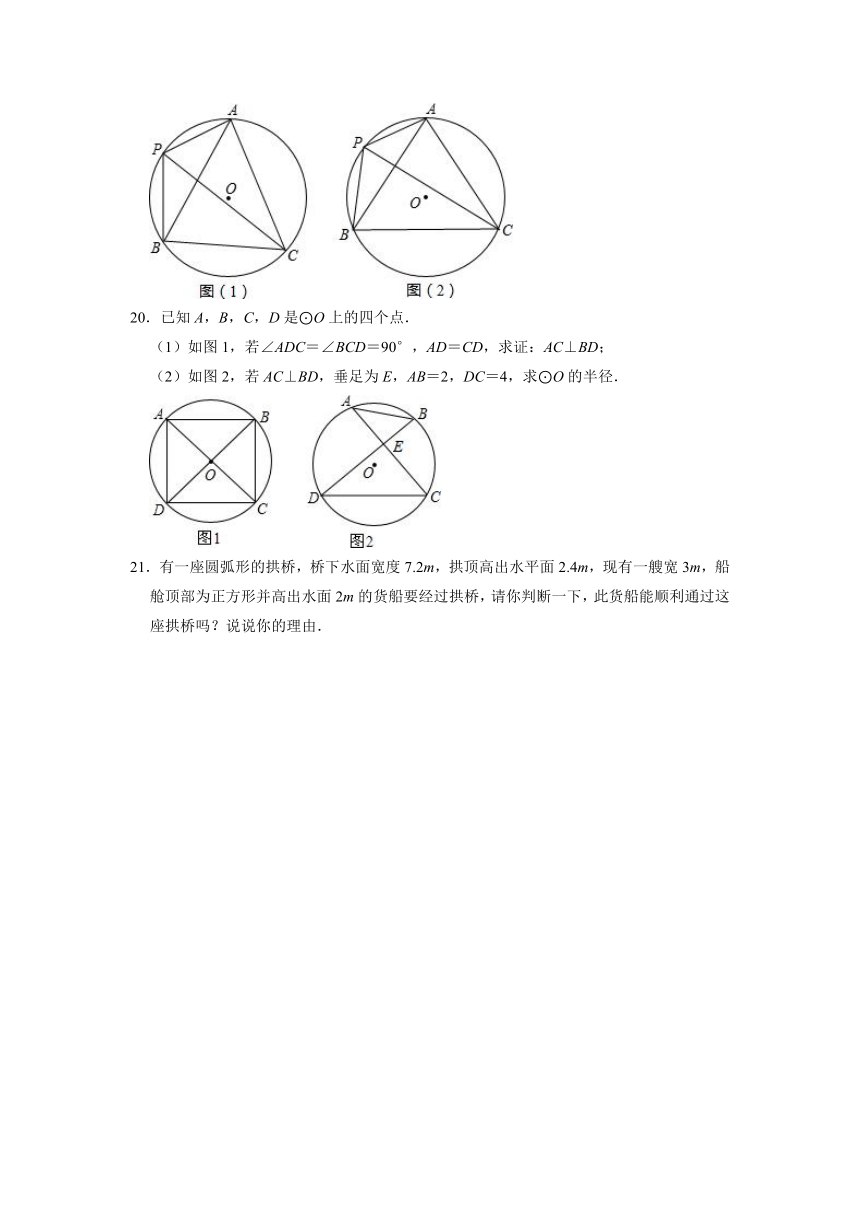
20.已知A,B,C,D是⊙O上的四个点.
(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.
21.有一座圆弧形的拱桥,桥下水面宽度7.2m,拱顶高出水平面2.4m,现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船要经过拱桥,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
参考答案
1.解:过O作OC⊥AB于C,
∵OC过O,
∴AC=BC=AB=12,
在Rt△AOC中,由勾股定理得:OC==5.
故选:B.
2.解:连接OA,OC,过点O作OD⊥AC于点D,
∵∠AOC=2∠B,且∠AOD=∠COD=∠AOC,
∴∠COD=∠B=60°;
在Rt△COD中,OC=4,∠COD=60°,
∴CD=OC=2,
∴AC=2CD=4.
故选:A.
3.解:∵OD⊥BC,
∴BD=CD=BC=×12=6,
在Rt△BOD中,∵OB=AB=8,BD=6,
∴OD==2,
∴S△OBD=OD BD=×2×6=6.
故选:A.
4.解:A、根据垂径定理不能推出AC=AB,故A选项错误;
B、∵直径CD⊥弦AB,
∴=,
∵对的圆周角是∠C,对的圆心角是∠BOD,
∴∠BOD=2∠C,故B选项正确;
C、不能推出∠C=∠B,故C选项错误;
D、不能推出∠A=∠BOD,故D选项错误;
故选:B.
5.解:∵⊙O的直径AB⊥CD于点E,
∴CE=DE,弧CB=弧BD,
在△OCE和△ODE中,
,
∴△OCE≌△ODE,
故选:B.
6.解:如图,连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4cm,OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3cm,
∴CM=OC+OM=5+3=8cm,
∴AC===4cm;
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2cm,
在Rt△AMC中,AC===2cm.
故选:C.
7.解:如图所示,
连接OB、OC,过O作OD⊥BC于D,
∵⊙O的面积为2π
∴⊙O的半径为
∵△ABC为正三角形,
∴∠BOC==120°,∠BOD=∠BOC=60°,OB=,
∴BD=OB sin∠BOD==,
∴BC=2BD=,
∴OD=OB cos∠BOD= cos60°=,
∴△BOC的面积= BC OD=××=,
∴△ABC的面积=3S△BOC=3×=.
故选:C.
8.解:如图,由题意得:OP=,OP⊥AB,且AB=6;
∴BP=AP=3;由勾股定理得:
OB2=OP2+BP2=3+9=12,
∴⊙O的面积=π OB2=12π,
故选:D.
9.解:如图,作AD⊥BC于D,
∵AB=AC=5,
∴AD垂直平分BC,
∴点O在直线AD上,
连接OB,
在Rt△ABD中,sinB==,
∵AB=5,
∴AD=4,
∴BD==3,
在Rt△OBD中,OB=,BD=3,
∴OD==1,
当点A与点O在BC的两侧时,OA=AD+OD=4+1=5;
当点A与点O在BC的同侧时,OA=AD﹣OD=4﹣1=3,
故OA的长为3或5.
故选:A.
10.解:作OC⊥AB于C,连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=×8=4,
在Rt△AOC中,OA=5,
∴OC===3,
即圆心O到AB的距离为3.
故答案为:3.
11.解:(1)过点C作CM⊥x轴于点M,则MA=MB,连接AC,如图
∵点C的坐标为(2,),
∴OM=2,CM=,
在Rt△ACM中,CA=2,
∴AM==1,
∴OA=OM﹣AM=1,OB=OM+BM=3,
∴A点坐标为(1,0),B点坐标为(3,0);
(2)将A(1,0),B(3,0)代入y=x2+bx+c得
,
解得.
所以二次函数的解析式为y=x2﹣4x+3.
12.(1)证明:∵AD是⊙O的直径,
∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,
,
∴Rt△ABD≌Rt△ACD(HL),
∴∠BAD=∠CAD,
∵AB=AC,
∴BE=CE;
(2)四边形BFCD是菱形.
证明:∵AD是直径,AB=AC,
∴AD⊥BC,BE=CE,
∵CF∥BD,
∴∠FCE=∠DBE,
在△BED和△CEF中,
,
∴△BED≌△CEF(ASA),
∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,
∵∠AEC=∠CED,∠CAE=∠ECD,
∴△AEC∽△CED,
∴=,
∴CE2=DE AE,
设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD===2.
13.解:∵OE⊥AB,
∴∠OEF=90°,
∵OC为小圆的直径,
∴∠OFC=90°,
而∠EOF=∠FOC,
∴Rt△OEF∽Rt△OFC,
∴OE:OF=OF:OC,即4:6=6:OC,
∴⊙O的半径OC=9;
在Rt△OCF中,OF=6,OC=9,
∴CF==3,
∵OF⊥CD,
∴CF=DF,
∴CD=2CF=6.
14.(1)证明:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解:由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE===2,AE===8,
∴AC=AE﹣CE=8﹣2.
15.解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设OB=x,
又∵BE=4,
∴x2=(x﹣4)2+82,
解得:x=10,
∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=30°.
16.解:(1)∵∠PBC=∠D,∠PBC=∠C,
∴∠C=∠D,
∴CB∥PD;
(2)连接OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴=,
∵∠PBC=∠DCB=22.5°,
∴∠BOC=∠BOD=2∠C=45°,
∴∠AOC=180°﹣∠BOC=135°,
∴劣弧AC的长为:=.
17.(1)证明:作OC⊥AB于点C,
∵OC⊥AB,
∴AC=BC,
∵AE=BF,
∴EC=FC,
∵OC⊥EF,
∴OE=OF,
∵∠EOF=60°,
∴△OEF是等边三角形;
(2)解:∵在等边△OEF中,∠OEF=∠EOF=60°,AE=OE,
∴∠A=∠AOE=30°,
∴∠AOF=90°,
∵AO=10,
∴OF=,
∴S△AOF=××10=,S扇形AOD=×102=25π,
∴S阴影=S扇形AOD﹣S△AOF=25π﹣.
18.解:(1)如图,过点O作OE⊥AC于E,
则AE=AC=×2=1,
∵翻折后点D与圆心O重合,
∴OE=r,
在Rt△AOE中,AO2=AE2+OE2,
即r2=12+(r)2,
解得r=;
(2)连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质,所对的圆周角为∠B,所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.
19.解:(1)∵∠BPC=60°
∴∠BAC=60°,
∵AB=AC,
∴△ABC为等边三角形,
∴∠ACB=∠ABC=60°,
∴∠APC=∠ABC=60°,
而点P是的中点,
∴∠ACP=∠ACB=30°,
∴∠PAC=90°,
∴tan∠PCA==tan30°=,
∴AC=PA;
(2)过A点作AD⊥BC交BC于D,连接OP交AB于E,如图,
∵AB=AC,
∴AD平分BC,
∴点O在AD上,
连接OB,则∠BOD=∠BAC,
∵∠BPC=∠BAC,
∴sin∠BOD=sin∠BPC==,
设OB=25x,则BD=24x,
∴OD==7x,
在Rt△ABD中,AD=25x+7x=32x,BD=24x,
∴AB==40x,
∵点P是的中点,
∴OP垂直平分AB,
∴AE=AB=20x,∠AEP=∠AEO=90°,
在Rt△AEO中,OE==15x,
∴PE=OP﹣OE=25x﹣15x=10x,
在Rt△APE中,tan∠PAE===,
即tan∠PAB的值为.
20.解:(1)∵∠ADC=∠BCD=90°,
∴AC、BD是⊙O的直径,
∴∠DAB=∠ABC=90°,
∴四边形ABCD是矩形,
∵AD=CD,
∴四边形ABCD是正方形,
∴AC⊥BD;
(2)连接DO,延长交圆O于F,连接CF、BF.
∵DF是直径,
∴∠DCF=∠DBF=90°,
∴FB⊥DB,
又∵AC⊥BD,
∴BF∥AC,∠BDC+∠ACD=90°,
∵∠FCA+∠ACD=90°
∴∠BDC=∠FCA=∠BAC
∴四边形ACFB是等腰梯形,
∴CF=AB.
根据勾股定理,得
CF2+DC2=AB2+DC2=DF2=20,
∴DF=,
∴OD=,即⊙O的半径为.
21.解:如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=7.2m,
∴BD=AB=3.6m.
又∵CD=2.4m,
设OB=OC=ON=r,则OD=(r﹣2.4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,解得r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面AB=2m,
∴CE=2.4﹣2=0.4(m),
∴OE=r﹣CE=3.9﹣0.4=3.5(m),
在Rt△OEN中,EN2=ON2﹣OE2=3.92﹣3.52=2.96(m2),
∴EN=(m).
∴MN=2EN=2×≈3.44m>3m.
∴此货船能顺利通过这座拱桥.
1.如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
A.6 B.5 C.4 D.3
2.如图,⊙O是△ABC的外接圆,∠B=60°,⊙O的半径为4,则AC的长等于( )
A.4 B.6 C.2 D.8
3.如图,AB为圆O的直径,BC为圆O的一弦,自O点作BC的垂线,且交BC于D点.若AB=16,BC=12,则△OBD的面积为何?( )
A.6 B.12 C.15 D.30
4.如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
A.AC=AB B.∠C=∠BOD C.∠C=∠B D.∠A=∠BOD
5.如图,已知⊙O的直径AB⊥CD于点E,则下列结论不一定成立的是( )
A.CE=DE B.AE=OE C.= D.△OCE≌△ODE
6.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB=8cm,且AB⊥CD,垂足为M,则AC的长为( )
A.cm B.cm C.cm或cm D.cm或cm
7.已知⊙O的面积为2π,则其内接正三角形的面积为( )
A.3 B.3 C. D.
8.在⊙O内有一点P,已知OP=,且圆内过点P的最短弦长为6,则⊙O的面积是( )
A.6π B.8π C.10π D.12π
9.在△ABC中,AB=AC=5,sinB=,⊙O过点B、C两点,且⊙O半径r=,则OA的长为( )
A.3或5 B.5 C.4或5 D.4
10.如图,在⊙O中,已知半径为5,弦AB的长为8,那么圆心O到AB的距离为 .
11.如图,平面直角坐标系中,以点C(2,)为圆心,以2为半径的圆与x轴交于A,B两点.
(1)求A,B两点的坐标;
(2)若二次函数y=x2+bx+c的图象经过点A,B,试确定此二次函数的解析式.
12.如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
13.如图,在⊙O中,半径OC与弦AB垂直,垂足为E,以OC为直径的圆与弦AB的一个交点为F,D是CF延长线与⊙O的交点.若OE=4,OF=6,求⊙O的半径和CD的长.
14.已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆心O到直线AB的距离为6,求AC的长.
15.如图,AB是⊙O的直径,弦CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.
16.如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O上,PB与CD交于点F,∠PBC=∠C.
(1)求证:CB∥PD;
(2)若∠PBC=22.5°,⊙O的半径R=2,求劣弧AC的长度.
17.已知:如图,AB是⊙O的弦,⊙O的半径为10,OE、OF分别交AB于点E、F,OF的延长线交⊙O于点D,且AE=BF,∠EOF=60°.
(1)求证:△OEF是等边三角形;
(2)当AE=OE时,求阴影部分的面积.(结果保留根号和π)
18.在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连接CD.
(1)如图1,若点D与圆心O重合,AC=2,求⊙O的半径r;
(2)如图2,若点D与圆心O不重合,∠BAC=25°,请直接写出∠DCA的度数.
19.如图,已知△ABC是⊙O的内接三角形,AB=AC,点P是的中点,连接PA,PB,PC.
(1)如图①,若∠BPC=60°.求证:AC=AP;
(2)如图②,若sin∠BPC=,求tan∠PAB的值.
20.已知A,B,C,D是⊙O上的四个点.
(1)如图1,若∠ADC=∠BCD=90°,AD=CD,求证:AC⊥BD;
(2)如图2,若AC⊥BD,垂足为E,AB=2,DC=4,求⊙O的半径.
21.有一座圆弧形的拱桥,桥下水面宽度7.2m,拱顶高出水平面2.4m,现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船要经过拱桥,请你判断一下,此货船能顺利通过这座拱桥吗?说说你的理由.
参考答案
1.解:过O作OC⊥AB于C,
∵OC过O,
∴AC=BC=AB=12,
在Rt△AOC中,由勾股定理得:OC==5.
故选:B.
2.解:连接OA,OC,过点O作OD⊥AC于点D,
∵∠AOC=2∠B,且∠AOD=∠COD=∠AOC,
∴∠COD=∠B=60°;
在Rt△COD中,OC=4,∠COD=60°,
∴CD=OC=2,
∴AC=2CD=4.
故选:A.
3.解:∵OD⊥BC,
∴BD=CD=BC=×12=6,
在Rt△BOD中,∵OB=AB=8,BD=6,
∴OD==2,
∴S△OBD=OD BD=×2×6=6.
故选:A.
4.解:A、根据垂径定理不能推出AC=AB,故A选项错误;
B、∵直径CD⊥弦AB,
∴=,
∵对的圆周角是∠C,对的圆心角是∠BOD,
∴∠BOD=2∠C,故B选项正确;
C、不能推出∠C=∠B,故C选项错误;
D、不能推出∠A=∠BOD,故D选项错误;
故选:B.
5.解:∵⊙O的直径AB⊥CD于点E,
∴CE=DE,弧CB=弧BD,
在△OCE和△ODE中,
,
∴△OCE≌△ODE,
故选:B.
6.解:如图,连接AC,AO,
∵⊙O的直径CD=10cm,AB⊥CD,AB=8cm,
∴AM=AB=×8=4cm,OD=OC=5cm,
当C点位置如图1所示时,
∵OA=5cm,AM=4cm,CD⊥AB,
∴OM===3cm,
∴CM=OC+OM=5+3=8cm,
∴AC===4cm;
当C点位置如图2所示时,同理可得OM=3cm,
∵OC=5cm,
∴MC=5﹣3=2cm,
在Rt△AMC中,AC===2cm.
故选:C.
7.解:如图所示,
连接OB、OC,过O作OD⊥BC于D,
∵⊙O的面积为2π
∴⊙O的半径为
∵△ABC为正三角形,
∴∠BOC==120°,∠BOD=∠BOC=60°,OB=,
∴BD=OB sin∠BOD==,
∴BC=2BD=,
∴OD=OB cos∠BOD= cos60°=,
∴△BOC的面积= BC OD=××=,
∴△ABC的面积=3S△BOC=3×=.
故选:C.
8.解:如图,由题意得:OP=,OP⊥AB,且AB=6;
∴BP=AP=3;由勾股定理得:
OB2=OP2+BP2=3+9=12,
∴⊙O的面积=π OB2=12π,
故选:D.
9.解:如图,作AD⊥BC于D,
∵AB=AC=5,
∴AD垂直平分BC,
∴点O在直线AD上,
连接OB,
在Rt△ABD中,sinB==,
∵AB=5,
∴AD=4,
∴BD==3,
在Rt△OBD中,OB=,BD=3,
∴OD==1,
当点A与点O在BC的两侧时,OA=AD+OD=4+1=5;
当点A与点O在BC的同侧时,OA=AD﹣OD=4﹣1=3,
故OA的长为3或5.
故选:A.
10.解:作OC⊥AB于C,连接OA,如图,
∵OC⊥AB,
∴AC=BC=AB=×8=4,
在Rt△AOC中,OA=5,
∴OC===3,
即圆心O到AB的距离为3.
故答案为:3.
11.解:(1)过点C作CM⊥x轴于点M,则MA=MB,连接AC,如图
∵点C的坐标为(2,),
∴OM=2,CM=,
在Rt△ACM中,CA=2,
∴AM==1,
∴OA=OM﹣AM=1,OB=OM+BM=3,
∴A点坐标为(1,0),B点坐标为(3,0);
(2)将A(1,0),B(3,0)代入y=x2+bx+c得
,
解得.
所以二次函数的解析式为y=x2﹣4x+3.
12.(1)证明:∵AD是⊙O的直径,
∴∠ABD=∠ACD=90°,
在Rt△ABD和Rt△ACD中,
,
∴Rt△ABD≌Rt△ACD(HL),
∴∠BAD=∠CAD,
∵AB=AC,
∴BE=CE;
(2)四边形BFCD是菱形.
证明:∵AD是直径,AB=AC,
∴AD⊥BC,BE=CE,
∵CF∥BD,
∴∠FCE=∠DBE,
在△BED和△CEF中,
,
∴△BED≌△CEF(ASA),
∴CF=BD,
∴四边形BFCD是平行四边形,
∵∠BAD=∠CAD,
∴BD=CD,
∴四边形BFCD是菱形;
(3)解:∵AD是直径,AD⊥BC,BE=CE,
∵∠AEC=∠CED,∠CAE=∠ECD,
∴△AEC∽△CED,
∴=,
∴CE2=DE AE,
设DE=x,
∵BC=8,AD=10,
∴42=x(10﹣x),
解得:x=2或x=8(舍去)
在Rt△CED中,
CD===2.
13.解:∵OE⊥AB,
∴∠OEF=90°,
∵OC为小圆的直径,
∴∠OFC=90°,
而∠EOF=∠FOC,
∴Rt△OEF∽Rt△OFC,
∴OE:OF=OF:OC,即4:6=6:OC,
∴⊙O的半径OC=9;
在Rt△OCF中,OF=6,OC=9,
∴CF==3,
∵OF⊥CD,
∴CF=DF,
∴CD=2CF=6.
14.(1)证明:过O作OE⊥AB于点E,
则CE=DE,AE=BE,
∴BE﹣DE=AE﹣CE,即AC=BD;
(2)解:由(1)可知,OE⊥AB且OE⊥CD,连接OC,OA,
∴OE=6,
∴CE===2,AE===8,
∴AC=AE﹣CE=8﹣2.
15.解:(1)∵AB⊥CD,CD=16,
∴CE=DE=8,
设OB=x,
又∵BE=4,
∴x2=(x﹣4)2+82,
解得:x=10,
∴⊙O的直径是20.
(2)∵∠M=∠BOD,∠M=∠D,
∴∠D=∠BOD,
∵AB⊥CD,
∴∠D=30°.
16.解:(1)∵∠PBC=∠D,∠PBC=∠C,
∴∠C=∠D,
∴CB∥PD;
(2)连接OC,OD.
∵AB是⊙O的直径,弦CD⊥AB于点E,
∴=,
∵∠PBC=∠DCB=22.5°,
∴∠BOC=∠BOD=2∠C=45°,
∴∠AOC=180°﹣∠BOC=135°,
∴劣弧AC的长为:=.
17.(1)证明:作OC⊥AB于点C,
∵OC⊥AB,
∴AC=BC,
∵AE=BF,
∴EC=FC,
∵OC⊥EF,
∴OE=OF,
∵∠EOF=60°,
∴△OEF是等边三角形;
(2)解:∵在等边△OEF中,∠OEF=∠EOF=60°,AE=OE,
∴∠A=∠AOE=30°,
∴∠AOF=90°,
∵AO=10,
∴OF=,
∴S△AOF=××10=,S扇形AOD=×102=25π,
∴S阴影=S扇形AOD﹣S△AOF=25π﹣.
18.解:(1)如图,过点O作OE⊥AC于E,
则AE=AC=×2=1,
∵翻折后点D与圆心O重合,
∴OE=r,
在Rt△AOE中,AO2=AE2+OE2,
即r2=12+(r)2,
解得r=;
(2)连接BC,
∵AB是直径,
∴∠ACB=90°,
∵∠BAC=25°,
∴∠B=90°﹣∠BAC=90°﹣25°=65°,
根据翻折的性质,所对的圆周角为∠B,所对的圆周角为∠ADC,
∴∠ADC+∠B=180°,
∴∠B=∠CDB=65°,
∴∠DCA=∠CDB﹣∠A=65°﹣25°=40°.
19.解:(1)∵∠BPC=60°
∴∠BAC=60°,
∵AB=AC,
∴△ABC为等边三角形,
∴∠ACB=∠ABC=60°,
∴∠APC=∠ABC=60°,
而点P是的中点,
∴∠ACP=∠ACB=30°,
∴∠PAC=90°,
∴tan∠PCA==tan30°=,
∴AC=PA;
(2)过A点作AD⊥BC交BC于D,连接OP交AB于E,如图,
∵AB=AC,
∴AD平分BC,
∴点O在AD上,
连接OB,则∠BOD=∠BAC,
∵∠BPC=∠BAC,
∴sin∠BOD=sin∠BPC==,
设OB=25x,则BD=24x,
∴OD==7x,
在Rt△ABD中,AD=25x+7x=32x,BD=24x,
∴AB==40x,
∵点P是的中点,
∴OP垂直平分AB,
∴AE=AB=20x,∠AEP=∠AEO=90°,
在Rt△AEO中,OE==15x,
∴PE=OP﹣OE=25x﹣15x=10x,
在Rt△APE中,tan∠PAE===,
即tan∠PAB的值为.
20.解:(1)∵∠ADC=∠BCD=90°,
∴AC、BD是⊙O的直径,
∴∠DAB=∠ABC=90°,
∴四边形ABCD是矩形,
∵AD=CD,
∴四边形ABCD是正方形,
∴AC⊥BD;
(2)连接DO,延长交圆O于F,连接CF、BF.
∵DF是直径,
∴∠DCF=∠DBF=90°,
∴FB⊥DB,
又∵AC⊥BD,
∴BF∥AC,∠BDC+∠ACD=90°,
∵∠FCA+∠ACD=90°
∴∠BDC=∠FCA=∠BAC
∴四边形ACFB是等腰梯形,
∴CF=AB.
根据勾股定理,得
CF2+DC2=AB2+DC2=DF2=20,
∴DF=,
∴OD=,即⊙O的半径为.
21.解:如图,连接ON,OB.
∵OC⊥AB,
∴D为AB中点,
∵AB=7.2m,
∴BD=AB=3.6m.
又∵CD=2.4m,
设OB=OC=ON=r,则OD=(r﹣2.4)m.
在Rt△BOD中,根据勾股定理得:r2=(r﹣2.4)2+3.62,解得r=3.9.
∵CD=2.4m,船舱顶部为正方形并高出水面AB=2m,
∴CE=2.4﹣2=0.4(m),
∴OE=r﹣CE=3.9﹣0.4=3.5(m),
在Rt△OEN中,EN2=ON2﹣OE2=3.92﹣3.52=2.96(m2),
∴EN=(m).
∴MN=2EN=2×≈3.44m>3m.
∴此货船能顺利通过这座拱桥.
