2021-2022学年华师大版九年级下册27.1.3圆周角同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年华师大版九年级下册27.1.3圆周角同步练习(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 202.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 17:42:04 | ||
图片预览

文档简介
27.1.3 圆周角----华师大版九年级下册同步试卷
一、单选题
1.数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
A.勾股定理 B.直径所对的圆周角是直角
C.勾股定理的逆定理 D.90°的圆周角所对的弦是直径
2.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=36°,那么∠BAD等于( ).
A.36° B.44° C.54° D.56°
3.如图所示,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12个单位 B.10个单位 C.1个单位 D.15个单位
4.下列图形中的角是圆周角的是( )
A. B. C. D.
5.如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
A.82° B.38° C.24° D.41°
6.下列说法正确的是( )
A.等弧所对的圆周角相等 B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等 D.过弦的中点的直线必过圆心
7.如图,四边形内接于,为的直径,.若,则的大小是( )
A.55° B.70° C.110° D.140°
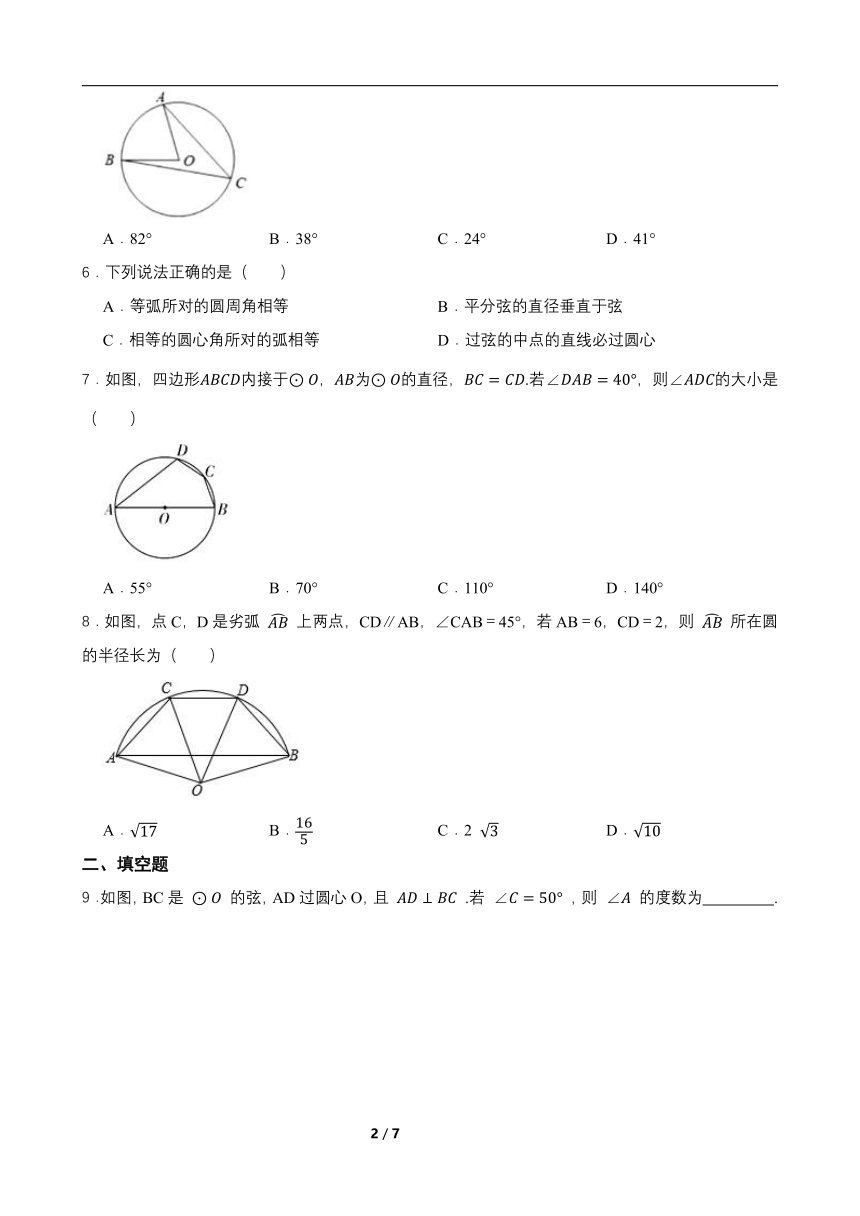
8.如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( )
A. B. C.2 D.
二、填空题
9.如图,BC是 的弦,AD过圆心O,且 .若 ,则 的度数为 .
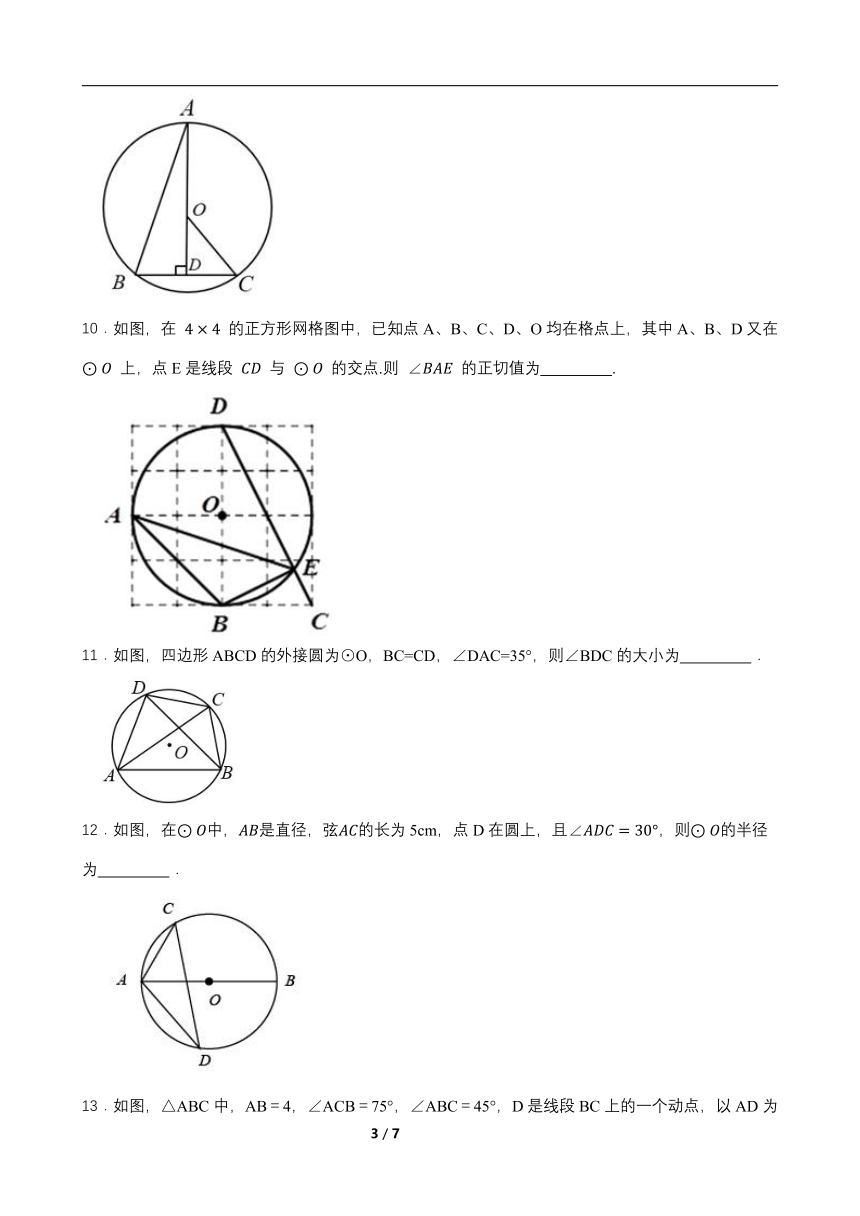
10.如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为 .
11.如图,四边形ABCD的外接圆为⊙O,BC=CD,∠DAC=35°,则∠BDC的大小为 .
12.如图,在中,是直径,弦的长为5cm,点D在圆上,且,则的半径为 .
13.如图,△ABC中,AB=4,∠ACB=75°,∠ABC=45°,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则EF的最小值为 .
三、解答题
14.如图,是的外接圆⊙O的直径,若∠ACB=50°,求∠BAD的度数.
15.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
答案解析部分
1.B
2.C
3.B
4.A
5.D
6.A
7.C
8.D
9.20
10.
11.35°
12.5cm
13.
14.解:如图,连接BD,
∵AD为△ABC的外接圆⊙O的直径,
∴∠ABD=90°,
∵∠D=∠C=50°,
∴∠BAD=90°-∠D=90°-50°=40°.
15.解:如图①,∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC=
∵AD平分∠CAB,
∴ ,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5 ;
(Ⅱ)如图②,连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB= ∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5. 1 / 3
一、单选题
1.数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
A.勾股定理 B.直径所对的圆周角是直角
C.勾股定理的逆定理 D.90°的圆周角所对的弦是直径
2.如图,AB是⊙O的直径,CD是⊙O的弦,如果∠ACD=36°,那么∠BAD等于( ).
A.36° B.44° C.54° D.56°
3.如图所示,小明同学设计了一个测量圆直径的工具,标有刻度的尺子OA,OB在O点钉在一起,并使它们保持垂直,在测直径时,把O点靠在圆周上,读得刻度OE=8个单位,OF=6个单位,则圆的直径为( )
A.12个单位 B.10个单位 C.1个单位 D.15个单位
4.下列图形中的角是圆周角的是( )
A. B. C. D.
5.如图,点A、B、C是⊙O上的三个点,若∠AOB=82°,则∠C的度数为( )
A.82° B.38° C.24° D.41°
6.下列说法正确的是( )
A.等弧所对的圆周角相等 B.平分弦的直径垂直于弦
C.相等的圆心角所对的弧相等 D.过弦的中点的直线必过圆心
7.如图,四边形内接于,为的直径,.若,则的大小是( )
A.55° B.70° C.110° D.140°
8.如图,点C,D是劣弧 上两点,CD∥AB,∠CAB=45°,若AB=6,CD=2,则 所在圆的半径长为( )
A. B. C.2 D.
二、填空题
9.如图,BC是 的弦,AD过圆心O,且 .若 ,则 的度数为 .
10.如图,在 的正方形网格图中,已知点A、B、C、D、O均在格点上,其中A、B、D又在 上,点E是线段 与 的交点.则 的正切值为 .
11.如图,四边形ABCD的外接圆为⊙O,BC=CD,∠DAC=35°,则∠BDC的大小为 .
12.如图,在中,是直径,弦的长为5cm,点D在圆上,且,则的半径为 .
13.如图,△ABC中,AB=4,∠ACB=75°,∠ABC=45°,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则EF的最小值为 .
三、解答题
14.如图,是的外接圆⊙O的直径,若∠ACB=50°,求∠BAD的度数.
15.已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D.
(Ⅰ)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(Ⅱ)如图②,若∠CAB=60°,求BD的长.
答案解析部分
1.B
2.C
3.B
4.A
5.D
6.A
7.C
8.D
9.20
10.
11.35°
12.5cm
13.
14.解:如图,连接BD,
∵AD为△ABC的外接圆⊙O的直径,
∴∠ABD=90°,
∵∠D=∠C=50°,
∴∠BAD=90°-∠D=90°-50°=40°.
15.解:如图①,∵BC是⊙O的直径,
∴∠CAB=∠BDC=90°.
∵在直角△CAB中,BC=10,AB=6,
∴由勾股定理得到:AC=
∵AD平分∠CAB,
∴ ,
∴CD=BD.
在直角△BDC中,BC=10,CD2+BD2=BC2,
∴易求BD=CD=5 ;
(Ⅱ)如图②,连接OB,OD.
∵AD平分∠CAB,且∠CAB=60°,
∴∠DAB= ∠CAB=30°,
∴∠DOB=2∠DAB=60°.
又∵OB=OD,
∴△OBD是等边三角形,
∴BD=OB=OD.
∵⊙O的直径为10,则OB=5,
∴BD=5. 1 / 3
