8.3 利用二元一次方程组解决较复杂的实际问题(第2课时) 课件(共33页)
文档属性
| 名称 | 8.3 利用二元一次方程组解决较复杂的实际问题(第2课时) 课件(共33页) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 17:29:18 | ||
图片预览









文档简介
(共33张PPT)
人教版 七年级下
精品同步教学课件
8.3实际问题与二元一次方程组
第2课时 利用二元一次方程组解决实际问题
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
一、比例问题
典例分析
例1:根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
⑴大瓶数
小瓶数
⑵大瓶所装消毒液
小瓶所装消毒液
总生产量.
典例分析
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
解得:
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
í
ì
=
+
22500000
250
500
y
x
x : y=2 : 5
例1:根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
二、配套问题
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
典例分析
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
设生产螺钉的10人,生产螺母的12人.
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
典例分析
练习:课本p102第4题
三、运输问题
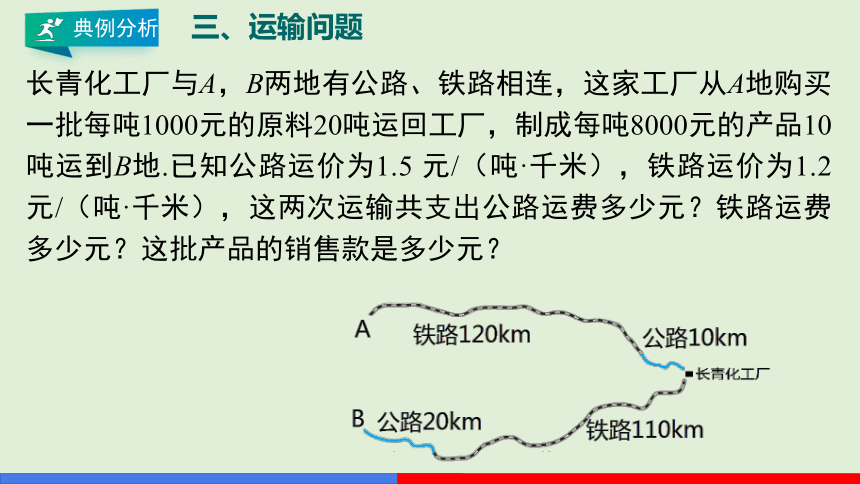
长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料20吨运回工厂,制成每吨8000元的产品10吨运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费多少元?铁路运费多少元?这批产品的销售款是多少元?
典例分析
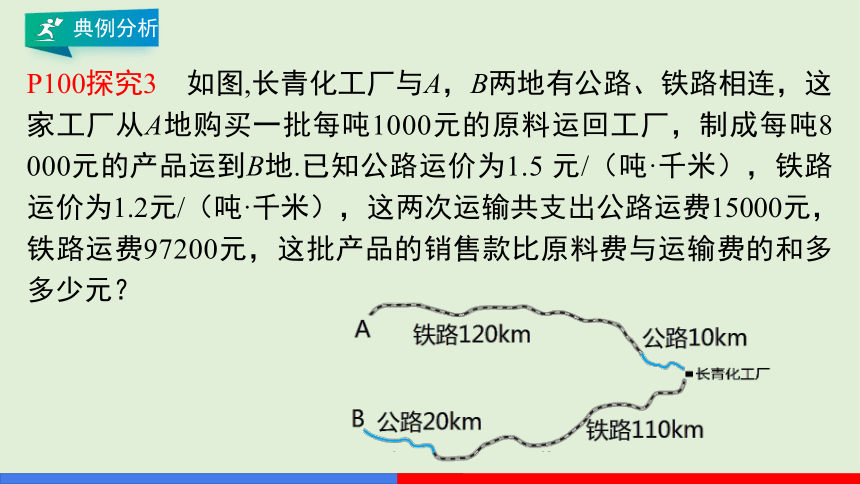
P100探究3 如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
典例分析
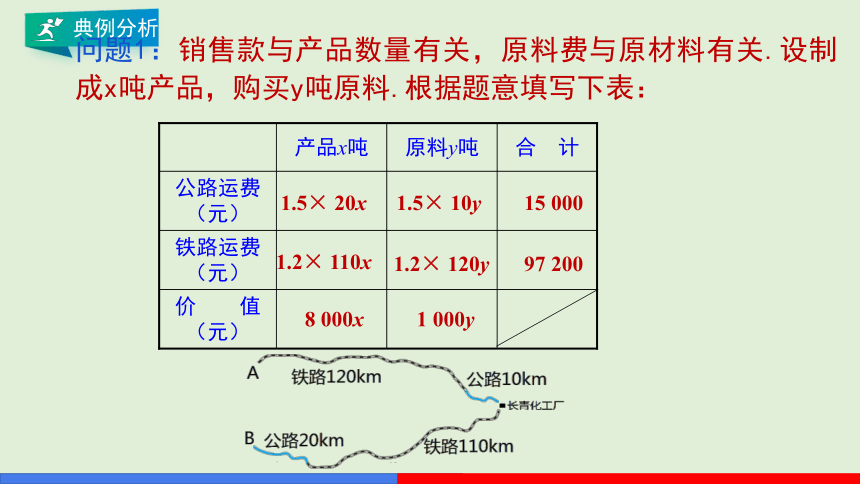
问题1:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
典例分析
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8000x-1000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元).
这批产品的销售款比原料费与运输费的和多1 887 800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
2x+ y=1000
11x+ 12y=8100.
整理方程组得
典例分析
练习 一批蔬菜要运往批发市场,菜农准备用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表示.
甲种货车(辆) 乙种货车(辆) 总量(吨)
第一次 4 5 28.5
第二次 3 6 27
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完.如果每吨付20元运费,问:菜农应付运费多少元?
解:设甲种货车运
吨,乙种货车运 吨.
根据题意,得
解得
所以
答:菜农应付500元.
3. 某商品原来每件零售价是 a 元,现在每件降
价10%,降价后每件零售价是 元.
4. 某种品牌的彩电降价20%以后,每台售价为
a元,则该品牌彩电每台原价应为 元.
1. 商品原价200元,九折出售,售价是 元.
5. 某商品按定价的八折出售,售价是12.8元,
则原定售价是 元.
2. 商品进价是150元,售价是180元,则利润是
元,利润率是_____.
180
30
20%
0.9a
1.25a
16
四、销售问题
典例分析
利润
利润率=
= 售价-进价
●售价、进价、利润的关系:
利润
●进价、利润、利润率的关系:
进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
要点归纳
1.某商场购进商品后,加价40% 作为销售价,商场搞优惠促销活动,决定甲、乙两件商品分别以七折和九折销售. 某顾客购买甲、乙两件商品,共付款399 元,这两件商品原销售价之和为490 元. 这两件商品的进价分别为多少元?
典例分析
1.某商场购进商品后,加价40% 作为销售价,商场搞优惠促销活动,决定甲、乙两件商品分别以七折和九折销售. 某顾客购买甲、乙两件商品,共付款399 元,这两件商品原销售价之和为490 元. 这两件商品的进价分别为多少元?
典例分析
甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
五、行程问题——相遇追及问题
典例分析
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
即甲的速度为5km/h,乙的速度为3km/h.
甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
六、行程问题——上下坡问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
典例分析
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700m.
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
七、航行问题-顺水逆水问题
典例分析
练习:某船顺流航行36km用3h,逆流航行24km用3 h,则水流速度和船在静水中的速度各是多少?
解得
答:船在静水中的速度为10km/h,水流速度为2km/h.
某城市为了缓解缺水状况,实施了一项引水工程,要把200 km 以外的一条大河的水引到城市中来. 这个工程被交给了甲、乙两个施工队,两队合作,工期为50 天. 甲、乙两队合作了30 天后,乙队因另外有任务需要离开10 天,于是甲队加快速度,每天多修0.6 km ;10 天后乙队回来,为了保证工期,甲队保持现在的速度不变,乙队每天比原来多修0.4 km,结果如期完成. 问:甲、乙两队原计划每天各修多少千米?
八、工程问题
典例分析
解:设一辆大货车、一辆小货车一次分别可运货x 吨,y 吨.
由题意得 解得
所以4×3+2.5×5=24.5(吨).
答:3辆大货车与5辆小货车一次可以运货24.5吨.
典例分析
从甲地到乙地有一段上坡与一段平路. 如果保持上坡每小时走3 km,平路每小时走4 km,下坡每小时走5 km,那么从甲地到乙地需54 min,从乙地到甲地需42 min.甲地到乙地全程是多少?
1.
解:设从甲地到乙地上坡的路程为x km,平路的路程为y km.
备选习题
由题意得 解得
所以甲地到乙地全程是
答:甲地到乙地全程是 km.
备选习题
用含药30%和75%的两种防腐药水,配制含药50%的防腐药水18 kg,两种药水各需多少千克?
2.
解:设需用含药30%防腐药水x千克,含药75%的防腐药水y 千克.
由题意得 解得
答:两种药水分别需要10千克,8千克.
备选习题
打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花多少钱?
3.
解:设打折前A商品每件x元,B商品每件y元.
由题意得 解得
500×16+500×4-9600=400(元).
答:比不打折少花400元.
备选习题
某家商店的账目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元.这个记录是否有误?如果有误,请说明理由.
4.
解:设牙刷每支x元,牙膏每盒y元.
由题意得 即
方程组无解,所以这个记录有误.
备选习题
https://www.21cnjy.com/help/help_extract.php
人教版 七年级下
精品同步教学课件
8.3实际问题与二元一次方程组
第2课时 利用二元一次方程组解决实际问题
课件栏目及使用说明:本课件适用于常规同步教学课堂,面向基础水平的学生使用。课件包括以下环节:
新知引入
典例分析
自主学习
随堂练习
拓展提高
课堂小结
备选习题
一、比例问题
典例分析
例1:根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
等量关系:
⑴大瓶数
小瓶数
⑵大瓶所装消毒液
小瓶所装消毒液
总生产量.
典例分析
解:设这些消毒液应该分装x大瓶、y小瓶.
根据题意可列方程组:
解得:
答:这些消毒液应该分装20000大瓶和50000小瓶.
①
②
í
ì
=
+
22500000
250
500
y
x
x : y=2 : 5
例1:根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?
二、配套问题
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
分析: 将题中出现的量在表格中呈现
产品类型 所需人数 生产总量
螺钉 x
螺母 y
螺母总产量是螺钉的2倍
人数和为22人
1200x
2000y
典例分析
解:设生产螺钉的x人,生产螺母的y人.
依题意,可列方程组:
解方程组,得
设生产螺钉的10人,生产螺母的12人.
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母. 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应各安排多少名工人生产螺钉和螺母?
典例分析
练习:课本p102第4题
三、运输问题
长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料20吨运回工厂,制成每吨8000元的产品10吨运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费多少元?铁路运费多少元?这批产品的销售款是多少元?
典例分析
P100探究3 如图,长青化工厂与A,B两地有公路、铁路相连,这家工厂从A地购买一批每吨1000元的原料运回工厂,制成每吨8 000元的产品运到B地.已知公路运价为1.5 元/(吨·千米),铁路运价为1.2元/(吨·千米),这两次运输共支出公路运费15000元,铁路运费97200元,这批产品的销售款比原料费与运输费的和多多少元?
典例分析
问题1:销售款与产品数量有关,原料费与原材料有关.设制成x吨产品,购买y吨原料.根据题意填写下表:
1.5× 20x
1.2× 110x
8 000x
1.5× 10y
1.2× 120y
1 000y
15 000
97 200
价 值(元)
铁路运费(元)
公路运费(元)
合 计
原料y吨
产品x吨
典例分析
解:根据图表,列出方程组
解方程组得
x=300,
y=400.
8000x-1000y-15 000-97 200
=8000×300-1 000×400-15 000-97 200
=1 887 800(元).
这批产品的销售款比原料费与运输费的和多1 887 800元.
1.5 × 20x+ 1.5×10y=15 000,
1.2 × 110x+ 1.2×120y=97 200.
2x+ y=1000
11x+ 12y=8100.
整理方程组得
典例分析
练习 一批蔬菜要运往批发市场,菜农准备用汽车公司的甲、乙两种货车.已知过去两次租用这两种货车的记录如下表示.
甲种货车(辆) 乙种货车(辆) 总量(吨)
第一次 4 5 28.5
第二次 3 6 27
这批蔬菜需租用5辆甲种货车、2辆乙种货车刚好一次运完.如果每吨付20元运费,问:菜农应付运费多少元?
解:设甲种货车运
吨,乙种货车运 吨.
根据题意,得
解得
所以
答:菜农应付500元.
3. 某商品原来每件零售价是 a 元,现在每件降
价10%,降价后每件零售价是 元.
4. 某种品牌的彩电降价20%以后,每台售价为
a元,则该品牌彩电每台原价应为 元.
1. 商品原价200元,九折出售,售价是 元.
5. 某商品按定价的八折出售,售价是12.8元,
则原定售价是 元.
2. 商品进价是150元,售价是180元,则利润是
元,利润率是_____.
180
30
20%
0.9a
1.25a
16
四、销售问题
典例分析
利润
利润率=
= 售价-进价
●售价、进价、利润的关系:
利润
●进价、利润、利润率的关系:
进价
×100%
折扣数
●标价、折扣数、商品售价的关系:
商品售价=
标价×
10
●商品售价、进价、利润率的关系:
商品进价
商品售价=
×(1+利润率)
要点归纳
1.某商场购进商品后,加价40% 作为销售价,商场搞优惠促销活动,决定甲、乙两件商品分别以七折和九折销售. 某顾客购买甲、乙两件商品,共付款399 元,这两件商品原销售价之和为490 元. 这两件商品的进价分别为多少元?
典例分析
1.某商场购进商品后,加价40% 作为销售价,商场搞优惠促销活动,决定甲、乙两件商品分别以七折和九折销售. 某顾客购买甲、乙两件商品,共付款399 元,这两件商品原销售价之和为490 元. 这两件商品的进价分别为多少元?
典例分析
甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
分析:(1) 同时出发,同向而行
甲出发点
乙出发点
4km
甲追上乙
乙2h行程
甲2h行程
甲2h行程=4km+乙2h行程
(2) 同时出发,相向而行
甲出发点
乙出发点
4km
相遇地
甲0.5h
行程
乙0.5h
行程
甲0.5h行程+乙0.5h行程=4km
五、行程问题——相遇追及问题
典例分析
解:设甲、乙的速度分别为xkm/h,ykm/h.
根据题意,得
解方程组,得
即甲的速度为5km/h,乙的速度为3km/h.
甲、乙两人相距4km,以各自的速度同时出发.如果同向而行,甲2h追上乙;如果相向而行,两人0.5h后相遇.试问两人的速度各是多少?
六、行程问题——上下坡问题
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
典例分析
平路时间 坡路时间 总时间
上学
放学
解:设小华家到学校平路长x m,下坡路长y m.
根据题意,可列方程组:
解方程组,得
答:小明家到学校的距离为700m.
小华从家里到学校的路是一段平路和一段下坡路. 假设他始终保持平路每分钟走60m,下坡路每分钟走80m,上坡路每分钟走40m,则他从家里到学校需10min,从学校到家里需15min.问小华家离学校多远?
我国的长江由西至东奔腾不息,其中九江至南京约有450千米的路程,某船从九江出发9个小时就能到达南京;返回时则用多了1个小时.求此船在静水中的速度以及长江水的平均流速.
解:设轮船在静水中的速度为x千米/时,长江水的平均流速为y千米/时.
答:轮船在静水中的速度为47.5千米/时,长江水的平均流速为2.5千米/时.
七、航行问题-顺水逆水问题
典例分析
练习:某船顺流航行36km用3h,逆流航行24km用3 h,则水流速度和船在静水中的速度各是多少?
解得
答:船在静水中的速度为10km/h,水流速度为2km/h.
某城市为了缓解缺水状况,实施了一项引水工程,要把200 km 以外的一条大河的水引到城市中来. 这个工程被交给了甲、乙两个施工队,两队合作,工期为50 天. 甲、乙两队合作了30 天后,乙队因另外有任务需要离开10 天,于是甲队加快速度,每天多修0.6 km ;10 天后乙队回来,为了保证工期,甲队保持现在的速度不变,乙队每天比原来多修0.4 km,结果如期完成. 问:甲、乙两队原计划每天各修多少千米?
八、工程问题
典例分析
解:设一辆大货车、一辆小货车一次分别可运货x 吨,y 吨.
由题意得 解得
所以4×3+2.5×5=24.5(吨).
答:3辆大货车与5辆小货车一次可以运货24.5吨.
典例分析
从甲地到乙地有一段上坡与一段平路. 如果保持上坡每小时走3 km,平路每小时走4 km,下坡每小时走5 km,那么从甲地到乙地需54 min,从乙地到甲地需42 min.甲地到乙地全程是多少?
1.
解:设从甲地到乙地上坡的路程为x km,平路的路程为y km.
备选习题
由题意得 解得
所以甲地到乙地全程是
答:甲地到乙地全程是 km.
备选习题
用含药30%和75%的两种防腐药水,配制含药50%的防腐药水18 kg,两种药水各需多少千克?
2.
解:设需用含药30%防腐药水x千克,含药75%的防腐药水y 千克.
由题意得 解得
答:两种药水分别需要10千克,8千克.
备选习题
打折前,买60件A商品和30件B商品用了1080元,买50件A商品和10件B商品用了840元.打折后,买500件A商品和500件B商品用了9600元,比不打折少花多少钱?
3.
解:设打折前A商品每件x元,B商品每件y元.
由题意得 解得
500×16+500×4-9600=400(元).
答:比不打折少花400元.
备选习题
某家商店的账目记录显示,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元.这个记录是否有误?如果有误,请说明理由.
4.
解:设牙刷每支x元,牙膏每盒y元.
由题意得 即
方程组无解,所以这个记录有误.
备选习题
https://www.21cnjy.com/help/help_extract.php
