2021-2022学年人教版七年级数学下册5.2.2平行线的判定同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年人教版七年级数学下册5.2.2平行线的判定同步练习(Word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 238.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 19:05:48 | ||
图片预览


文档简介
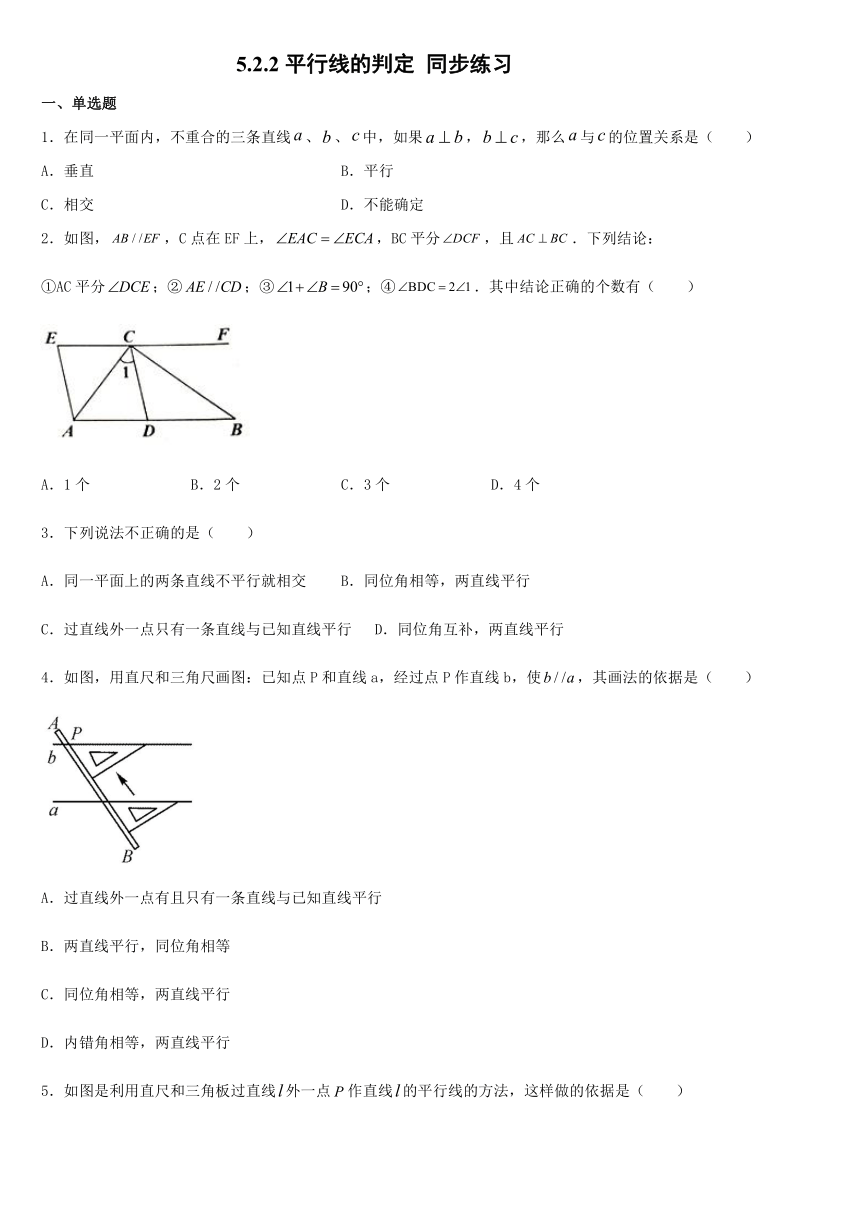
5.2.2平行线的判定 同步练习
一、单选题
1.在同一平面内,不重合的三条直线、、中,如果,,那么与的位置关系是( )
A.垂直 B.平行
C.相交 D.不能确定
2.如图,,C点在EF上,,BC平分,且.下列结论:
①AC平分;②;③;④.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法不正确的是( )
A.同一平面上的两条直线不平行就相交 B.同位角相等,两直线平行
C.过直线外一点只有一条直线与已知直线平行 D.同位角互补,两直线平行
4.如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使,其画法的依据是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.两直线平行,同位角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
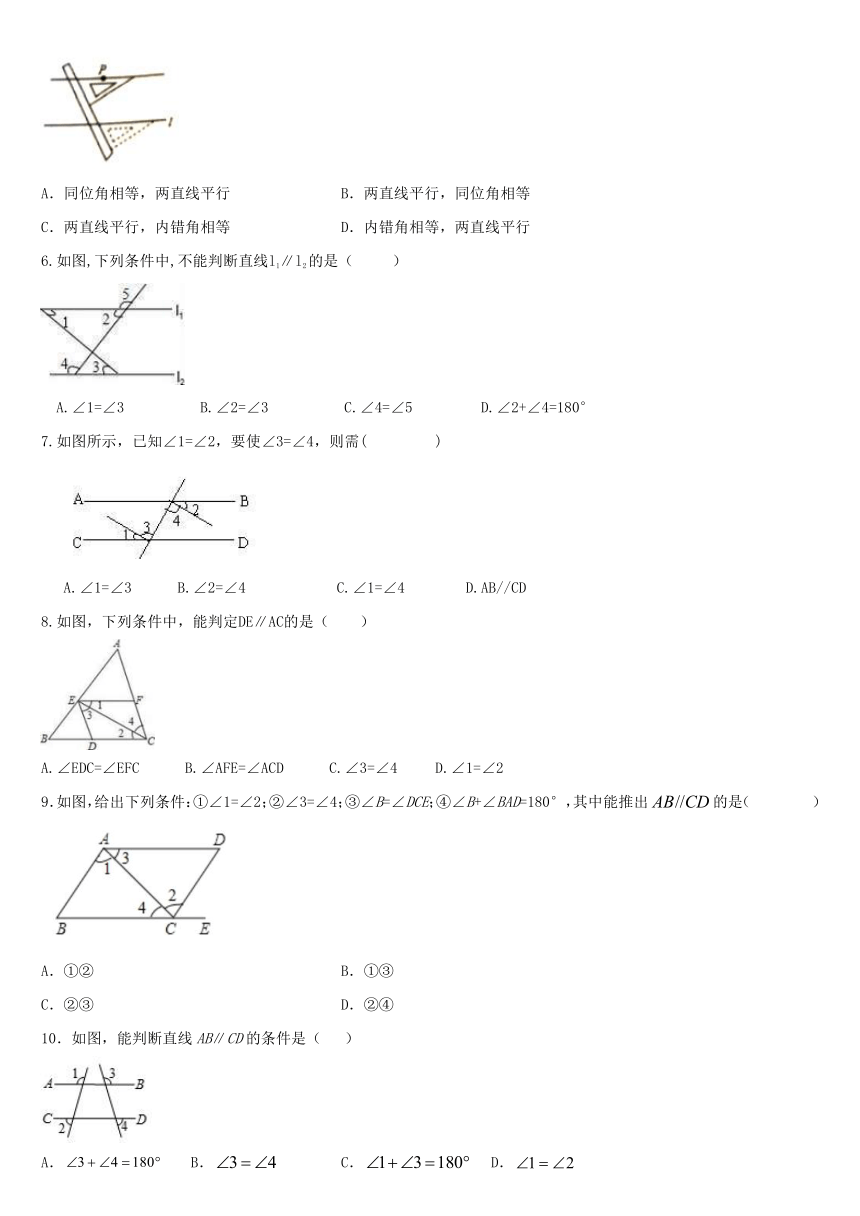
5.如图是利用直尺和三角板过直线外一点作直线的平行线的方法,这样做的依据是( )
A.同位角相等,两直线平行 B.两直线平行,同位角相等
C.两直线平行,内错角相等 D.内错角相等,两直线平行
6.如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
7.如图所示,已知∠1=∠2,要使∠3=∠4,则需( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.AB//CD
8.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2
9.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出的是( )
A.①② B.①③
C.②③ D.②④
10.如图,能判断直线AB∥CD的条件是( )
A. B. C. D.
二、填空题
11.下图是我们常用的画平行线的方法,三角板的平移构造了平行线的判定依据:“___________,两直线平行.”
12.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
13.如图,点E是BA延长线上一点,下列条件中:①∠1=∠3;②∠5=∠D;③∠2=∠4;④∠B+∠BCD=180°,能判定ABCD的有___.(填序号)
14.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
15.己知为平面内三条不同直线,若则与的位置关系是 _________
16.如图,直线 AB、CD 被直线 EF 所截,当满足条件___________时(只需写出一个你认为合适的条件),AB∥CD.
三、解答题
17.如图,∠1=∠3,∠1=∠2,那么DE与BC有怎样的位置关系?为什么?
18.如图,∠BAF=46°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
19.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
参考答案
1.B 2.D 3.D 4.C 5.A 6.B 7.D 8.C 9.B 10.A
11.同位角相等
12.a1∥a100;
13.②③④
14.平行
15.
16.(答案不唯一)
17.【答案】解:DE∥BC.理由如下 ;∵∠1=∠3,∠1=∠2,∴∠2=∠3(等量代换)∴DE∥BC(内错角相等,两直线平行)。
【考点】平行线的判定
【解析】【分析】DE∥BC.理由如下 ;根据等量代换得出∠2=∠3 ,根据内错角相等二直线平行得出DE∥BC 。
18.【答案】解:CD∥AB.
证明:∵CE⊥CD,
∴∠DCE=90°,
∵∠ACE=136°,
∴∠ACD=360°﹣136°﹣90°=134°,
∵∠BAF=46°,
∴∠BAC=180°﹣∠BAF=180°﹣46°=134°,
∴∠ACD=∠BAC,
∴CD∥AB.
【考点】平行线的判定
【解析】【分析】根据已知条件求出关于直线CD,AB的内错角的度数,看它们是否相等,以此来判定两直线是否平行.
19.(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;.
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF.
一、单选题
1.在同一平面内,不重合的三条直线、、中,如果,,那么与的位置关系是( )
A.垂直 B.平行
C.相交 D.不能确定
2.如图,,C点在EF上,,BC平分,且.下列结论:
①AC平分;②;③;④.其中结论正确的个数有( )
A.1个 B.2个 C.3个 D.4个
3.下列说法不正确的是( )
A.同一平面上的两条直线不平行就相交 B.同位角相等,两直线平行
C.过直线外一点只有一条直线与已知直线平行 D.同位角互补,两直线平行
4.如图,用直尺和三角尺画图:已知点P和直线a,经过点P作直线b,使,其画法的依据是( )
A.过直线外一点有且只有一条直线与已知直线平行
B.两直线平行,同位角相等
C.同位角相等,两直线平行
D.内错角相等,两直线平行
5.如图是利用直尺和三角板过直线外一点作直线的平行线的方法,这样做的依据是( )
A.同位角相等,两直线平行 B.两直线平行,同位角相等
C.两直线平行,内错角相等 D.内错角相等,两直线平行
6.如图,下列条件中,不能判断直线l1∥l2的是( )
A.∠1=∠3 B.∠2=∠3 C.∠4=∠5 D.∠2+∠4=180°
7.如图所示,已知∠1=∠2,要使∠3=∠4,则需( )
A.∠1=∠3 B.∠2=∠4 C.∠1=∠4 D.AB//CD
8.如图,下列条件中,能判定DE∥AC的是( )
A.∠EDC=∠EFC B.∠AFE=∠ACD C.∠3=∠4 D.∠1=∠2
9.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④∠B+∠BAD=180°,其中能推出的是( )
A.①② B.①③
C.②③ D.②④
10.如图,能判断直线AB∥CD的条件是( )
A. B. C. D.
二、填空题
11.下图是我们常用的画平行线的方法,三角板的平移构造了平行线的判定依据:“___________,两直线平行.”
12.规律探究:同一平面内有直线a1,a2,a3…,a100,若a1⊥a2,a2∥a3,a3⊥a4…,按此规律,a1和a100的位置是________.
13.如图,点E是BA延长线上一点,下列条件中:①∠1=∠3;②∠5=∠D;③∠2=∠4;④∠B+∠BCD=180°,能判定ABCD的有___.(填序号)
14.如图所示,直线a,b被c所截,∠1=30°,∠2:∠3=1:5,则直线a与b的位置关系是________.
15.己知为平面内三条不同直线,若则与的位置关系是 _________
16.如图,直线 AB、CD 被直线 EF 所截,当满足条件___________时(只需写出一个你认为合适的条件),AB∥CD.
三、解答题
17.如图,∠1=∠3,∠1=∠2,那么DE与BC有怎样的位置关系?为什么?
18.如图,∠BAF=46°,∠ACE=136°,CE⊥CD.问CD∥AB吗?为什么?
19.如图,∠ADE+∠BCF=180°,BE平分∠ABC,∠ABC=2∠E.
(1)AD与BC平行吗?请说明理由;
(2)AB与EF的位置关系如何?为什么?
参考答案
1.B 2.D 3.D 4.C 5.A 6.B 7.D 8.C 9.B 10.A
11.同位角相等
12.a1∥a100;
13.②③④
14.平行
15.
16.(答案不唯一)
17.【答案】解:DE∥BC.理由如下 ;∵∠1=∠3,∠1=∠2,∴∠2=∠3(等量代换)∴DE∥BC(内错角相等,两直线平行)。
【考点】平行线的判定
【解析】【分析】DE∥BC.理由如下 ;根据等量代换得出∠2=∠3 ,根据内错角相等二直线平行得出DE∥BC 。
18.【答案】解:CD∥AB.
证明:∵CE⊥CD,
∴∠DCE=90°,
∵∠ACE=136°,
∴∠ACD=360°﹣136°﹣90°=134°,
∵∠BAF=46°,
∴∠BAC=180°﹣∠BAF=180°﹣46°=134°,
∴∠ACD=∠BAC,
∴CD∥AB.
【考点】平行线的判定
【解析】【分析】根据已知条件求出关于直线CD,AB的内错角的度数,看它们是否相等,以此来判定两直线是否平行.
19.(1)AD∥BC,
理由是:∵∠ADE+∠BCF=180°,∠ADE+∠ADF=180°,
∴∠ADF=∠BCF,
∴AD∥BC;.
(2)AB∥EF,
理由是:∵BE平分∠ABC,
∴∠ABC=2∠ABE,
∵∠ABC=2∠E,
∴∠ABE=∠E,
∴AB∥EF.
