2021-2022学年苏科版八年级数学下册7.4频数分布表和频数分布直方图同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版八年级数学下册7.4频数分布表和频数分布直方图同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 412.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 19:11:19 | ||
图片预览




文档简介
7.4频数分布表和频数分布直方图
一、选择题
1、在频数分布表中,各小组的频数之和( )
A.小于数据总个数 B.等于数据总个数 C.大于数据总个数 D.不能确定
2、一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分 ( )
A.10组 B.9组 C.8组 D.7组
3、现有一组数据,最大值为93,最小值为22,现要把它分成6组,则下列组距中,合适的为 ( )
A. 9 B. 12 C. 15 D. 18
4、某棉纺厂为了了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表,则棉花纤维长度的数据在8≤x<32这个范围的频率为( )
棉花纤维长度x 频数
0≤x<8 1
8≤x<16 2
16≤x<24 8
24≤x<32 6
32≤x<40 3
A.0.8 B.0.7 C.0.4 D.0.2
5、某校为了了解七年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数直方图(每组含前一个边界值,不含后一个边界值),请根据图示计算仰卧起坐次数在15~20次之间的频数是( )
A.3 B.5 C.10 D.12
6.学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
A. 0.1 B. 0.15 C. 0.25 D. 0.3
7.为了了解噪声污染的情况,某市环保局抽样调查了80个测量点的噪声声级(单位:分贝),并进行整理后分成五组,绘制出频数分布直方图,如图所示.已知从左至右前四组的频率分别是0.15,0.25,0.3,0.2,且噪声声级高于69.5分贝就会影响工作和生活,那么影响到工作和生活而需对附近区域进行治理的测量点有( )
A. 5个 B. 8个 C. 12个 D. 15个
8.某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中
数据不在分点上,对图中提供的信息作出如下的判断:
②成绩在79.5~89.5分段的人数占30%;
③成绩在79.5分以上的学生有20人;
④本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A. 4个 B. 3个 C. 2个 D. 1个
9、小杰调查了本班同学的体重情况,画出频数直方图如图所示,下列结论中,错误的是( )
A. 全班总人数为45人
B. 体重在50~55 kg的人数最多
C. “45~50 kg”这一组的频率比“60~65 kg”这一组的大0.1
D. 体重在60~65 kg的人数占全班总人数的
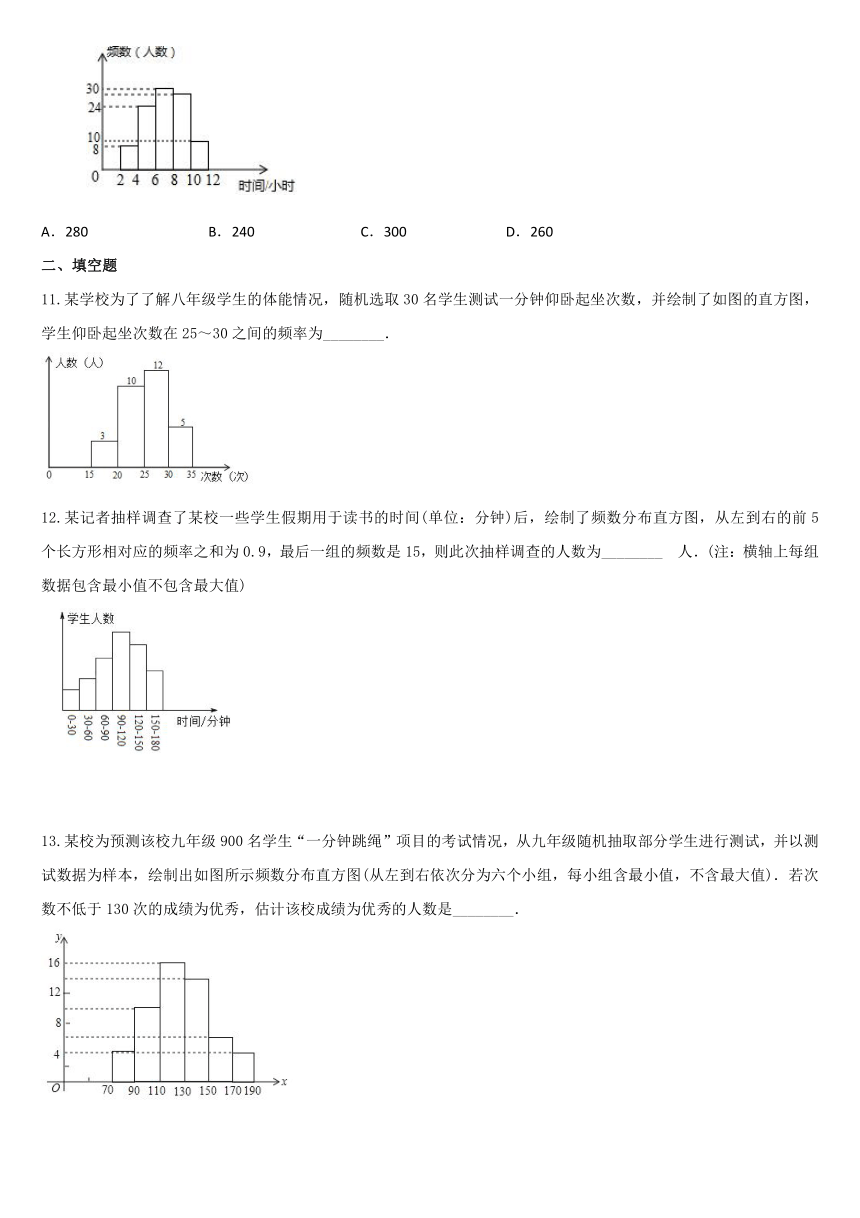
10、为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280 B.240 C.300 D.260
二、填空题
11.某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在25~30之间的频率为________.
12.某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为________ 人.(注:横轴上每组数据包含最小值不包含最大值)
13.某校为预测该校九年级900名学生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分学生进行测试,并以测试数据为样本,绘制出如图所示频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值).若次数不低于130次的成绩为优秀,估计该校成绩为优秀的人数是________.
14.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有 人.
15、一个容量为60的样本,样本中最大值是172,最小值是150,取组距为3,则该样本可以分为 组
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
17、某地区中考现场考试内容有两项,50米跑为必考项目,另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试.王老师对参加体育中考的九(1)班40名学生的一项选测科目作了统计,列出如图所示的统计表,则本班参加坐位体前屈的人数是 人.
组别 立定跳远 坐位体前屈 实心球 一分钟跳绳
频率 0.4 0.35 0.1 0.15
18、空气质量指数,简称AQI,如果AQI在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最近一段时间的AQI画出的频数分布直方图如图所示.已知每天的AQI都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 %.
19、为了解某校七年级男生的身高情况,该校从七年级随机找来50名男生进行了身高测量,根据测量结果(均取整数,单位:cm)列出了下表.
分组 频数
151~155 3
156~160 4
161~165 12
166~170 13
171~175 12
176~180 4
181以上 2
合计 50
根据表中提供的信息回答下列问题:
(1)数据在161~165范围内的频数是 ;
(2)频数最大的一组数据的范围是 ;
(3)估计该校七年级男生身高在176 cm(包括176 cm)以上的约占
三、解答题
20、如图是某市某校教职工年龄(取正整数)的频数直方图(每组包括最小值,不包括最大值),根据图中提供的信息解答下列问题:
(1)该校教职工共有多少人?
(2)不小于25岁但小于40岁的教职工人数占教职工总人数的百分比是多少?
(3)如果35岁的教职工有4人,那么年龄在35岁以上的教职工有几人?
21、七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
(1)频数统计表中a= ,b= ;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.七(3)班“绿色奥运”知识竞赛成绩频数直方图
22.统计七年级若干名学生的跳高测试成绩,得到如图所示的频数分布直方图(每组数据含最小值,不含最大值).请回答下列问题:
(1)参加测试的总人数有多少人?若规定跳高高度超过1.09米为达标,则此次跳高达标率为多少?(精确到1%)
(2)数据分组的组距是多少?
(3)频数最大的一组的频率是多少(精确到0.01)?该组的两个边界值分别是多少?
23.某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 频数/人 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(1)在频数分布表中,a=________,b=________;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.
24.我市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a=________,b=________;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?
25、某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次,第一次月考后,选取了其中一个A层次班级的考试成绩分布情况进行处理分析,制成频数分布表(成绩得分均为整数):
根据表中提供的信息解答下列各题:
(1)频数分布表中的a= ,b= ,c= ;
(2)将频数分布直方图补充完整;
(3)小明正好在所选取的班级中,他认为:学校八年级共有20个班(平均每班40人),根据本班的成绩分布情况可知,在这次考试中,全年级90分以上为优秀,则优秀的人数约为 人,60分及以上为及格,及格的人数约为 人,及格的百分比约为 ;
(4)小明得到的数据会与实际情况相符吗?为什么?
(答案)
一、选择题
1-10. BABAA DBACA
二、填空题
11.答案为:0.4.
12.答案为:150.
13.答案为:400.
14.答案为:90.
15、一个容量为60的样本,样本中最大值是172,最小值是150,取组距为3,则该样本可以分为 8 组
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
【解答】解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是0.4.
故答案为:0.4.
17、某地区中考现场考试内容有两项,50米跑为必考项目,另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试.王老师对参加体育中考的九(1)班40名学生的一项选测科目作了统计,列出如图所示的统计表,则本班参加坐位体前屈的人数是 人.
组别 立定跳远 坐位体前屈 实心球 一分钟跳绳
频率 0.4 0.35 0.1 0.15
【解答】解:∵频率,
∴频数=频率×总数=0.35×40=14人.
故答案为14.
18、80.
19、为了解某校七年级男生的身高情况,该校从七年级随机找来50名男生进行了身高测量,根据测量结果(均取整数,单位:cm)列出了下表.
分组 频数
151~155 3
156~160 4
161~165 12
166~170 13
171~175 12
176~180 4
181以上 2
合计 50
根据表中提供的信息回答下列问题:
(1)数据在161~165范围内的频数是12 ;
(2)频数最大的一组数据的范围是166~170 ;
(3)估计该校七年级男生身高在176 cm(包括176 cm)以上的约占12%
三、解答题
20、如图是某市某校教职工年龄(取正整数)的频数直方图(每组包括最小值,不包括最大值),根据图中提供的信息解答下列问题:
(1)该校教职工共有多少人?
(2)不小于25岁但小于40岁的教职工人数占教职工总人数的百分比是多少?
(3)如果35岁的教职工有4人,那么年龄在35岁以上的教职工有几人?
解:(1)8+12+10+8+6+3+2+1=50(人),所以该校教职工共有50人.
(2)不小于25岁但小于40岁的教职工人数为12+10+8=30(人),
所以不小于25岁但小于40的教职工人数占教职工总人数的百分比是×100%=60%.
(3)年龄在35岁以上的教职工有(8-4)+6+3+2+1=16(人).
21、七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
(1)频数统计表中a= ,b= ;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.七(3)班“绿色奥运”知识竞赛成绩频数直方图
解答:(1)2 0.125
(2)直方图如图所示
(3)设获得一等奖学生为x人,获得二等奖学生为y人,根据题意得解得
9×50+20×30=1050元.
答:他们共获得奖金1050元.
22.【答案】 解:(1)总人数是:8+13+20+13=54(人),
此次跳高达标率是: %≈85.2%;
(2)组距是1.04﹣1.04=0.1(m).
(3)最大一组的频率是≈0.37.
该组的两个边界值是:1.19m和1.29m.
23.【答案】 (1)60;0.05
(2)解频数分布直方图如图所示,
(3)解:视力正常的人数占被调查人数的百分比是 ×100%=70%.
解:(1)总人数=20÷0.1=200.
∴a=200×0.3=60,b=1-0.1-0.2-0.35-0.3=0.05,
故答案为60,0.05.
24.【答案】 (1)6;0.2
(2)解:频数分布直方图为:
(3)解:1200×(1﹣0.1﹣0.25)=780,
所以估计全校每周在校参加经典诵读时间至少有4小时的学生约为780名.
解:(1)调查的总人数为4÷0.1=40(人),
a=40×0.15=6,
b= =0.2;
故答案为6,0.2
25、某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次,第一次月考后,选取了其中一个A层次班级的考试成绩分布情况进行处理分析,制成频数分布表(成绩得分均为整数):
根据表中提供的信息解答下列各题:
(1)频数分布表中的a= ,b= ,c= ;
(2)将频数分布直方图补充完整;
(3)小明正好在所选取的班级中,他认为:学校八年级共有20个班(平均每班40人),根据本班的成绩分布情况可知,在这次考试中,全年级90分以上为优秀,则优秀的人数约为 人,60分及以上为及格,及格的人数约为 人,及格的百分比约为 ;
(4)小明得到的数据会与实际情况相符吗?为什么?
【答案】解:(1)本次调查的有:2÷0.05=40(人),
a=40×0.20=8,b=40﹣2﹣4﹣8﹣10﹣6=10,c=10÷40=0.25,
故答案为:8,10,0.25;
(2)由(1)知,59.5~69.5的频数为8,79.5﹣89.5的频数为10,
补全的频数分布直方图如右图所示;
(3)优秀的人数约为:20×40×=120(人),
及格的人数约为:20×40×=680(人),
及格的百分比约为:=85%,
故答案为:120,680,85%;
(4)不相符,选择A层次班级的成绩不具有代表性.
一、选择题
1、在频数分布表中,各小组的频数之和( )
A.小于数据总个数 B.等于数据总个数 C.大于数据总个数 D.不能确定
2、一个容量为80的样本,最大值是141,最小值是50,取组距为10,则可以分 ( )
A.10组 B.9组 C.8组 D.7组
3、现有一组数据,最大值为93,最小值为22,现要把它分成6组,则下列组距中,合适的为 ( )
A. 9 B. 12 C. 15 D. 18
4、某棉纺厂为了了解一批棉花的质量,从中随机抽取了20根棉花纤维进行测量,其长度x(单位:mm)的数据分布如下表,则棉花纤维长度的数据在8≤x<32这个范围的频率为( )
棉花纤维长度x 频数
0≤x<8 1
8≤x<16 2
16≤x<24 8
24≤x<32 6
32≤x<40 3
A.0.8 B.0.7 C.0.4 D.0.2
5、某校为了了解七年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数直方图(每组含前一个边界值,不含后一个边界值),请根据图示计算仰卧起坐次数在15~20次之间的频数是( )
A.3 B.5 C.10 D.12
6.学校为了解七年级学生参加课外兴趣小组活动情况,随机调查了40名学生,将结果绘制成了如图所示的频数分布直方图,则参加绘画兴趣小组的频率是( )
A. 0.1 B. 0.15 C. 0.25 D. 0.3
7.为了了解噪声污染的情况,某市环保局抽样调查了80个测量点的噪声声级(单位:分贝),并进行整理后分成五组,绘制出频数分布直方图,如图所示.已知从左至右前四组的频率分别是0.15,0.25,0.3,0.2,且噪声声级高于69.5分贝就会影响工作和生活,那么影响到工作和生活而需对附近区域进行治理的测量点有( )
A. 5个 B. 8个 C. 12个 D. 15个
8.某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中
数据不在分点上,对图中提供的信息作出如下的判断:
②成绩在79.5~89.5分段的人数占30%;
③成绩在79.5分以上的学生有20人;
④本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A. 4个 B. 3个 C. 2个 D. 1个
9、小杰调查了本班同学的体重情况,画出频数直方图如图所示,下列结论中,错误的是( )
A. 全班总人数为45人
B. 体重在50~55 kg的人数最多
C. “45~50 kg”这一组的频率比“60~65 kg”这一组的大0.1
D. 体重在60~65 kg的人数占全班总人数的
10、为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,已知该校共有1000名学生,据此估计,该校五一期间参加社团活动时间在8~10小时之间的学生数大约是( )
A.280 B.240 C.300 D.260
二、填空题
11.某学校为了了解八年级学生的体能情况,随机选取30名学生测试一分钟仰卧起坐次数,并绘制了如图的直方图,学生仰卧起坐次数在25~30之间的频率为________.
12.某记者抽样调查了某校一些学生假期用于读书的时间(单位:分钟)后,绘制了频数分布直方图,从左到右的前5个长方形相对应的频率之和为0.9,最后一组的频数是15,则此次抽样调查的人数为________ 人.(注:横轴上每组数据包含最小值不包含最大值)
13.某校为预测该校九年级900名学生“一分钟跳绳”项目的考试情况,从九年级随机抽取部分学生进行测试,并以测试数据为样本,绘制出如图所示频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值).若次数不低于130次的成绩为优秀,估计该校成绩为优秀的人数是________.
14.某校学生“汉字听写”大赛成绩的频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩为“优良”(80分及以上)的学生有 人.
15、一个容量为60的样本,样本中最大值是172,最小值是150,取组距为3,则该样本可以分为 组
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
17、某地区中考现场考试内容有两项,50米跑为必考项目,另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试.王老师对参加体育中考的九(1)班40名学生的一项选测科目作了统计,列出如图所示的统计表,则本班参加坐位体前屈的人数是 人.
组别 立定跳远 坐位体前屈 实心球 一分钟跳绳
频率 0.4 0.35 0.1 0.15
18、空气质量指数,简称AQI,如果AQI在0~50空气质量类别为优,在51~100空气质量类别为良,在101~150空气质量类别为轻度污染,按照某市最近一段时间的AQI画出的频数分布直方图如图所示.已知每天的AQI都是整数,那么空气质量类别为优和良的天数占总天数的百分比为 %.
19、为了解某校七年级男生的身高情况,该校从七年级随机找来50名男生进行了身高测量,根据测量结果(均取整数,单位:cm)列出了下表.
分组 频数
151~155 3
156~160 4
161~165 12
166~170 13
171~175 12
176~180 4
181以上 2
合计 50
根据表中提供的信息回答下列问题:
(1)数据在161~165范围内的频数是 ;
(2)频数最大的一组数据的范围是 ;
(3)估计该校七年级男生身高在176 cm(包括176 cm)以上的约占
三、解答题
20、如图是某市某校教职工年龄(取正整数)的频数直方图(每组包括最小值,不包括最大值),根据图中提供的信息解答下列问题:
(1)该校教职工共有多少人?
(2)不小于25岁但小于40岁的教职工人数占教职工总人数的百分比是多少?
(3)如果35岁的教职工有4人,那么年龄在35岁以上的教职工有几人?
21、七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
(1)频数统计表中a= ,b= ;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.七(3)班“绿色奥运”知识竞赛成绩频数直方图
22.统计七年级若干名学生的跳高测试成绩,得到如图所示的频数分布直方图(每组数据含最小值,不含最大值).请回答下列问题:
(1)参加测试的总人数有多少人?若规定跳高高度超过1.09米为达标,则此次跳高达标率为多少?(精确到1%)
(2)数据分组的组距是多少?
(3)频数最大的一组的频率是多少(精确到0.01)?该组的两个边界值分别是多少?
23.某校为了解八年级学生的视力情况,对八年级的学生进行了一次视力调查,并将调查数据进行统计整理,绘制出如下频数分布表和频数分布直方图的一部分.
视力 频数/人 频率
4.0≤x<4.3 20 0.1
4.3≤x<4.6 40 0.2
4.6≤x<4.9 70 0.35
4.9≤x<5.2 a 0.3
5.2≤x<5.5 10 b
(1)在频数分布表中,a=________,b=________;
(2)将频数分布直方图补充完整;
(3)若视力在4.6以上(含4.6)均属正常,求视力正常的人数占被调查人数的百分比.
24.我市提倡“诵读中华经典,营造书香校园”的良好诵读氛围,促进校园文化建设,进而培养学生的良好诵读习惯,使经典之风浸漫校园.某中学为了了解学生每周在校经典诵读时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表,请根据图表信息解答下列问题:
时间(小时) 频数(人数) 频率
2≤t<3 4 0.1
3≤t<4 10 0.25
4≤t<5 a 0.15
5≤t<6 8 b
6≤t<7 12 0.3
合计 40 1
(1)表中的a=________,b=________;
(2)请将频数分布直方图补全;
(3)若该校共有1200名学生,试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名?
25、某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次,第一次月考后,选取了其中一个A层次班级的考试成绩分布情况进行处理分析,制成频数分布表(成绩得分均为整数):
根据表中提供的信息解答下列各题:
(1)频数分布表中的a= ,b= ,c= ;
(2)将频数分布直方图补充完整;
(3)小明正好在所选取的班级中,他认为:学校八年级共有20个班(平均每班40人),根据本班的成绩分布情况可知,在这次考试中,全年级90分以上为优秀,则优秀的人数约为 人,60分及以上为及格,及格的人数约为 人,及格的百分比约为 ;
(4)小明得到的数据会与实际情况相符吗?为什么?
(答案)
一、选择题
1-10. BABAA DBACA
二、填空题
11.答案为:0.4.
12.答案为:150.
13.答案为:400.
14.答案为:90.
15、一个容量为60的样本,样本中最大值是172,最小值是150,取组距为3,则该样本可以分为 8 组
16、小丽抽样调查了学校40名同学的体重(均精确到1kg),绘制了如图频数分布直方图,那么在该样本中体重不小于55kg的频率是 .
【解答】解:观察直方图可知:
因为该样本中体重不小于55kg的频数为:9+5+2=16,
所以该样本中体重不小于55kg的频率是0.4.
故答案为:0.4.
17、某地区中考现场考试内容有两项,50米跑为必考项目,另在立定跳远、坐位体前屈、实心球和一分钟跳绳中选一项测试.王老师对参加体育中考的九(1)班40名学生的一项选测科目作了统计,列出如图所示的统计表,则本班参加坐位体前屈的人数是 人.
组别 立定跳远 坐位体前屈 实心球 一分钟跳绳
频率 0.4 0.35 0.1 0.15
【解答】解:∵频率,
∴频数=频率×总数=0.35×40=14人.
故答案为14.
18、80.
19、为了解某校七年级男生的身高情况,该校从七年级随机找来50名男生进行了身高测量,根据测量结果(均取整数,单位:cm)列出了下表.
分组 频数
151~155 3
156~160 4
161~165 12
166~170 13
171~175 12
176~180 4
181以上 2
合计 50
根据表中提供的信息回答下列问题:
(1)数据在161~165范围内的频数是12 ;
(2)频数最大的一组数据的范围是166~170 ;
(3)估计该校七年级男生身高在176 cm(包括176 cm)以上的约占12%
三、解答题
20、如图是某市某校教职工年龄(取正整数)的频数直方图(每组包括最小值,不包括最大值),根据图中提供的信息解答下列问题:
(1)该校教职工共有多少人?
(2)不小于25岁但小于40岁的教职工人数占教职工总人数的百分比是多少?
(3)如果35岁的教职工有4人,那么年龄在35岁以上的教职工有几人?
解:(1)8+12+10+8+6+3+2+1=50(人),所以该校教职工共有50人.
(2)不小于25岁但小于40岁的教职工人数为12+10+8=30(人),
所以不小于25岁但小于40的教职工人数占教职工总人数的百分比是×100%=60%.
(3)年龄在35岁以上的教职工有(8-4)+6+3+2+1=16(人).
21、七年级(3)班学生参加学校组织的“绿色奥运”知识竞赛,老师将学生的成绩按10分的组距分段,统计每个分数段出现的频数,填入频数统计表,并绘制频数直方图.
(1)频数统计表中a= ,b= ;
(2)把频数直方图补充完整;
(3)学校设定成绩在69.5分以上的学生将获得一等奖或二等奖,一等奖奖励作业本15本及奖金50元,二等奖奖励作业本10本及奖金30元. 已知这部分学生共获得作业本335本,请你求出他们共获得的奖金.七(3)班“绿色奥运”知识竞赛成绩频数直方图
解答:(1)2 0.125
(2)直方图如图所示
(3)设获得一等奖学生为x人,获得二等奖学生为y人,根据题意得解得
9×50+20×30=1050元.
答:他们共获得奖金1050元.
22.【答案】 解:(1)总人数是:8+13+20+13=54(人),
此次跳高达标率是: %≈85.2%;
(2)组距是1.04﹣1.04=0.1(m).
(3)最大一组的频率是≈0.37.
该组的两个边界值是:1.19m和1.29m.
23.【答案】 (1)60;0.05
(2)解频数分布直方图如图所示,
(3)解:视力正常的人数占被调查人数的百分比是 ×100%=70%.
解:(1)总人数=20÷0.1=200.
∴a=200×0.3=60,b=1-0.1-0.2-0.35-0.3=0.05,
故答案为60,0.05.
24.【答案】 (1)6;0.2
(2)解:频数分布直方图为:
(3)解:1200×(1﹣0.1﹣0.25)=780,
所以估计全校每周在校参加经典诵读时间至少有4小时的学生约为780名.
解:(1)调查的总人数为4÷0.1=40(人),
a=40×0.15=6,
b= =0.2;
故答案为6,0.2
25、某校八年级根据学生的学习成绩、学习能力将学生依次分为A、B、C三个层次,第一次月考后,选取了其中一个A层次班级的考试成绩分布情况进行处理分析,制成频数分布表(成绩得分均为整数):
根据表中提供的信息解答下列各题:
(1)频数分布表中的a= ,b= ,c= ;
(2)将频数分布直方图补充完整;
(3)小明正好在所选取的班级中,他认为:学校八年级共有20个班(平均每班40人),根据本班的成绩分布情况可知,在这次考试中,全年级90分以上为优秀,则优秀的人数约为 人,60分及以上为及格,及格的人数约为 人,及格的百分比约为 ;
(4)小明得到的数据会与实际情况相符吗?为什么?
【答案】解:(1)本次调查的有:2÷0.05=40(人),
a=40×0.20=8,b=40﹣2﹣4﹣8﹣10﹣6=10,c=10÷40=0.25,
故答案为:8,10,0.25;
(2)由(1)知,59.5~69.5的频数为8,79.5﹣89.5的频数为10,
补全的频数分布直方图如右图所示;
(3)优秀的人数约为:20×40×=120(人),
及格的人数约为:20×40×=680(人),
及格的百分比约为:=85%,
故答案为:120,680,85%;
(4)不相符,选择A层次班级的成绩不具有代表性.
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
