2021--2022学年华东师大版九年级数学下册27.1.2圆的对称性同步试卷(Word版含答案)
文档属性
| 名称 | 2021--2022学年华东师大版九年级数学下册27.1.2圆的对称性同步试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 19:14:06 | ||
图片预览



文档简介
27.1.2 圆的对称性----华师大版九年级下册同步试卷
一、单选题
1.下列叙述正确的是( )
A.平分弦的直径必垂直于弦
B.同圆或等圆中,相等的弦所对的弧也相等
C.相等的圆心角所对的弧相等
D.相等的弧所对的弦相等
2.已知 是半径为6的圆的一条弦,则 的长不可能是( )
A.8 B.10 C.12 D.14
3.点P是 内一点,过点P的最长弦的长为 ,最短弦的长为 ,则OP的长为( )
A. B. C. D.
4.在 中,直径 ,弦 于点 ,若 ,则 的周长为( )
A.13 B.14 C.15 D.16
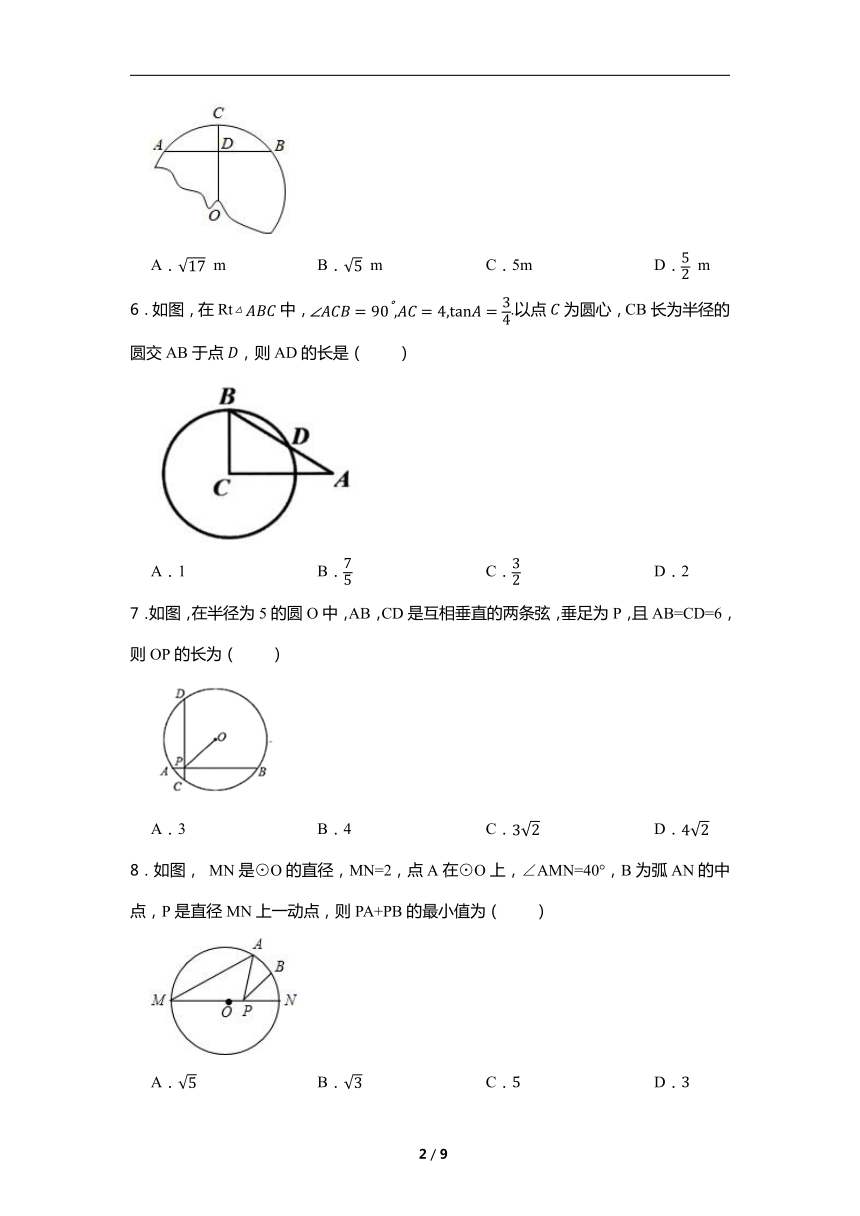
5.如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A. m B. m C.5m D. m
6.如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点,则AD的长是( )
A.1 B. C. D.2
7.如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=6,则OP的长为( )
A.3 B.4 C. D.
8.如图, MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B. C. D.
9.如图, 是 的弦(非直径),点C是弦 上的动点(不与点A,B重合),过点C作垂直于 的弦 .若设 的半径为r,弦 的长为a, ,则弦 的长( )
A.与r,a,m的值均有关 B.只与r,a的值有关
C.只与r,m的值有关 D.只与a,m的值有关
10.如图,AB为⊙O的直径,点C为⊙O上一点,连接CO,作AD OC,若CO= ,AC=2,则AD=( )
A.3 B. C. D.
二、填空题
11.如图,点A、B、C、D在⊙O上, ,则AC BD(填“>”“<”或“=”)
12.如图,在⊙O中, = ,则下列结论中:①AB=CD;②AC=BD;③∠AOC=∠BOD;④ = ,正确的是 填序号.
13.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕 的长为 cm.
14.如图,在⊙O中,=2,AD⊥OC于点D,比较大小AB 2AD.(填入“>”或“<”或“=”).
15.如图所示,草坪边上有互相垂直的小路m,n,垂足为E,草坪内有一个圆形花坛,花坛边缘有A,B,C三棵小树。在不踩踏草坪的前提下测圆形花坛的半径,某同学设计如下方案:若在小路上P,Q,K三点观测,发现均有两树与观测点在同一直线上,从E点沿着小路n往右走,测得∠1=∠2=∠3,EO=16米,OK=24米;从E点沿着小路m往上走,测得EP=15米,BP⊥m,则该圆的半径长为 米.
三、作图题
16.请仅用无刻度的直尺,根据条件完成下列画图.
(1)如图1, 内接于 , ,画出线段 的垂直平分线.
(2)如图2, 内接于 , , 、 分别为 和 的中点,画出线段 的垂直平分线.
四、解答题
17.如图所示,一座圆弧形拱桥的跨度AB长为40米,桥离水面最大距离CD为10米,若有一条水面上宽度为30米,宽度为6米的船能否通过这座桥?请说明理由.
18.如图,在△ABC中AB=5,AC=4,BC=2,以A为圆心,AB为半径作⊙A,延长BC交⊙A于点D,试求CD的长.
答案解析部分
1.D
2.D
3.B
4.D
5.D
6.B
7.D
8.B
9.D
10.D
11.=
12.①②③④
13.
14.=
15.
16.(1)解:如图1,直线 即为所求作的直线.
(2)解:如图2,直线 即为所求作的直线.
17.解:如图,假设船能通过,弧形桥所在的圆恢复如图,
在Rt△AOD中,r2=202+(r﹣10)2,
解得r=25,
∴OD=r﹣10=15,
在Rt△OEG中,r2=152+OG2,
解得OG=20,
∴可以通过的船的高度为GD=OG﹣OD=20﹣15=5,
∵6>5,
∴船不能通过.
18.解:如图,过点A作AE⊥BD于点E,连接AD.
∴AD=AB=5,
根据垂径定理,得DE=BE,
∴CE=BE﹣BC=DE﹣2.
根据勾股定理,得AD2﹣DE2=AC2﹣CE2
∴52﹣DE2=42﹣(DE﹣2)2
解得DE=
∴CD=DE+CE=2DE﹣2= 1 / 3
一、单选题
1.下列叙述正确的是( )
A.平分弦的直径必垂直于弦
B.同圆或等圆中,相等的弦所对的弧也相等
C.相等的圆心角所对的弧相等
D.相等的弧所对的弦相等
2.已知 是半径为6的圆的一条弦,则 的长不可能是( )
A.8 B.10 C.12 D.14
3.点P是 内一点,过点P的最长弦的长为 ,最短弦的长为 ,则OP的长为( )
A. B. C. D.
4.在 中,直径 ,弦 于点 ,若 ,则 的周长为( )
A.13 B.14 C.15 D.16
5.如图,破残的轮子上,弓形的弦AB为4m,高CD为1m,则这个轮子的半径长为( )
A. m B. m C.5m D. m
6.如图,在Rt中,.以点为圆心,CB长为半径的圆交AB于点,则AD的长是( )
A.1 B. C. D.2
7.如图,在半径为5的圆O中,AB,CD是互相垂直的两条弦,垂足为P,且AB=CD=6,则OP的长为( )
A.3 B.4 C. D.
8.如图, MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=40°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B. C. D.
9.如图, 是 的弦(非直径),点C是弦 上的动点(不与点A,B重合),过点C作垂直于 的弦 .若设 的半径为r,弦 的长为a, ,则弦 的长( )
A.与r,a,m的值均有关 B.只与r,a的值有关
C.只与r,m的值有关 D.只与a,m的值有关
10.如图,AB为⊙O的直径,点C为⊙O上一点,连接CO,作AD OC,若CO= ,AC=2,则AD=( )
A.3 B. C. D.
二、填空题
11.如图,点A、B、C、D在⊙O上, ,则AC BD(填“>”“<”或“=”)
12.如图,在⊙O中, = ,则下列结论中:①AB=CD;②AC=BD;③∠AOC=∠BOD;④ = ,正确的是 填序号.
13.如图,将半径为2cm的圆形纸片折叠后,圆弧恰好经过圆心O,则折痕 的长为 cm.
14.如图,在⊙O中,=2,AD⊥OC于点D,比较大小AB 2AD.(填入“>”或“<”或“=”).
15.如图所示,草坪边上有互相垂直的小路m,n,垂足为E,草坪内有一个圆形花坛,花坛边缘有A,B,C三棵小树。在不踩踏草坪的前提下测圆形花坛的半径,某同学设计如下方案:若在小路上P,Q,K三点观测,发现均有两树与观测点在同一直线上,从E点沿着小路n往右走,测得∠1=∠2=∠3,EO=16米,OK=24米;从E点沿着小路m往上走,测得EP=15米,BP⊥m,则该圆的半径长为 米.
三、作图题
16.请仅用无刻度的直尺,根据条件完成下列画图.
(1)如图1, 内接于 , ,画出线段 的垂直平分线.
(2)如图2, 内接于 , , 、 分别为 和 的中点,画出线段 的垂直平分线.
四、解答题
17.如图所示,一座圆弧形拱桥的跨度AB长为40米,桥离水面最大距离CD为10米,若有一条水面上宽度为30米,宽度为6米的船能否通过这座桥?请说明理由.
18.如图,在△ABC中AB=5,AC=4,BC=2,以A为圆心,AB为半径作⊙A,延长BC交⊙A于点D,试求CD的长.
答案解析部分
1.D
2.D
3.B
4.D
5.D
6.B
7.D
8.B
9.D
10.D
11.=
12.①②③④
13.
14.=
15.
16.(1)解:如图1,直线 即为所求作的直线.
(2)解:如图2,直线 即为所求作的直线.
17.解:如图,假设船能通过,弧形桥所在的圆恢复如图,
在Rt△AOD中,r2=202+(r﹣10)2,
解得r=25,
∴OD=r﹣10=15,
在Rt△OEG中,r2=152+OG2,
解得OG=20,
∴可以通过的船的高度为GD=OG﹣OD=20﹣15=5,
∵6>5,
∴船不能通过.
18.解:如图,过点A作AE⊥BD于点E,连接AD.
∴AD=AB=5,
根据垂径定理,得DE=BE,
∴CE=BE﹣BC=DE﹣2.
根据勾股定理,得AD2﹣DE2=AC2﹣CE2
∴52﹣DE2=42﹣(DE﹣2)2
解得DE=
∴CD=DE+CE=2DE﹣2= 1 / 3
