2021-2022学年华东师大版九年级下册27.3圆中的计算问题同步练习(Word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版九年级下册27.3圆中的计算问题同步练习(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 183.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 19:15:08 | ||
图片预览




文档简介
27.3 圆中的计算问题----华师大版九年级下册同步试卷
一、单选题
1.已知圆心角度数为60°,半径为30,则这个圆心角所对的弧长为( )
A.20π B.15π C.10π D.5π
2.已知扇形的半径为6,圆心角为10°,则扇形的面积为( )
A. B. C.π D.2π
3.三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则 的长为( )
A. B. C. D.
4. 如图,直径AB为3的半圆,绕A点逆时针旋转60°,此时点B到了点B′处,则图中阴影部分的面积是( )
A.3π B. C.6π D.24π
5.一个形如圆锥冰淇淋纸筒,其底面直径为6cm,母线长为10cm,围成这样的冰淇淋纸筒所需纸的面积是( )
A.60πcm2 B.15πcm2 C.28πcm2 D.30πcm2
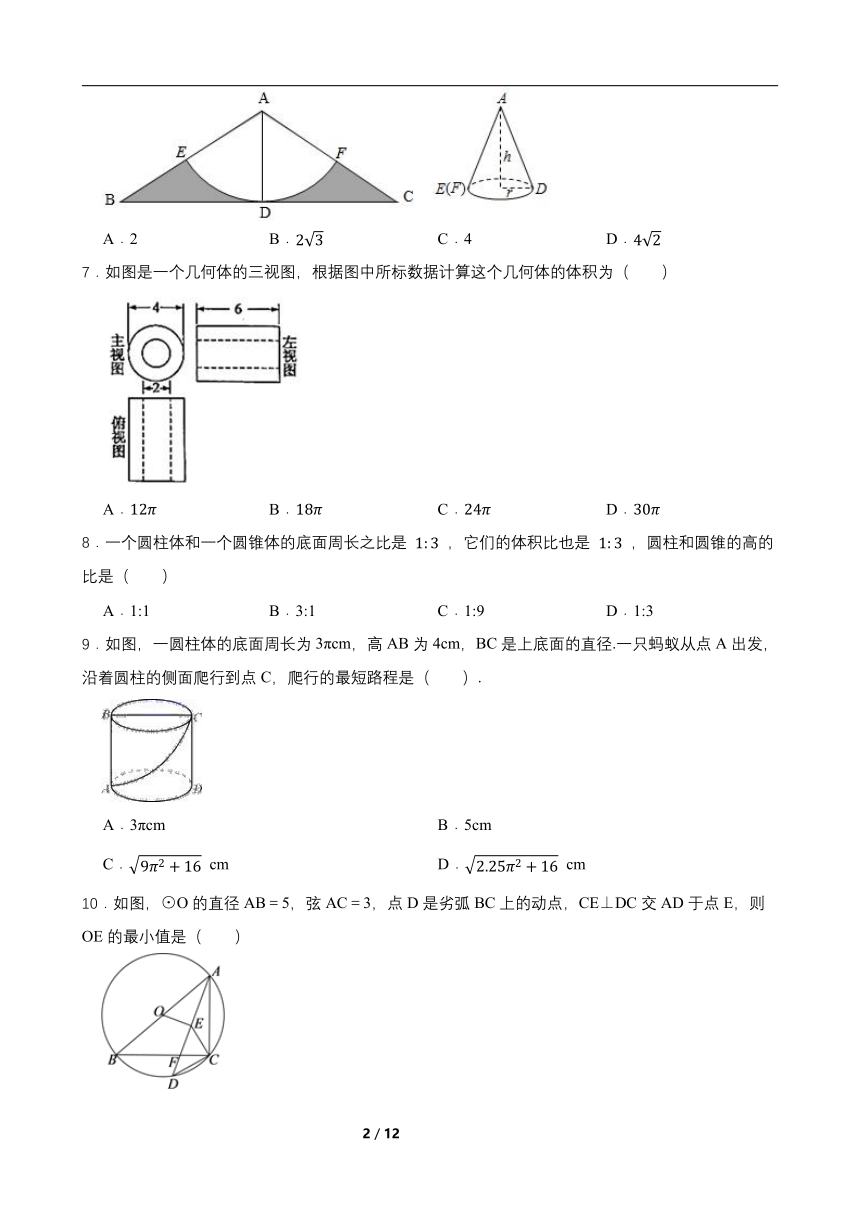
6.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
7.如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( )
A. B. C. D.
8.一个圆柱体和一个圆锥体的底面周长之比是 ,它们的体积比也是 ,圆柱和圆锥的高的比是( )
A.1:1 B.3:1 C.1:9 D.1:3
9.如图,一圆柱体的底面周长为3πcm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,爬行的最短路程是( ).
A.3πcm B.5cm
C. cm D. cm
10.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是( )
A. B. C.2- D. -1
二、填空题
11.己知弧的长是π,弧的半径为3,则该弧所对的圆心角度数为 °.
12.如图,扇形纸扇完全打开后,外侧两竹条AB,AC夹角为150°,AB的长为18cm,则弧BC的长为 cm.
13.一个扇形的圆心角为 ,面积为 ,则此扇形的半径长为 cm.
14.如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为4cm的等边三角形,点D是母线的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是 cm.
15.有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a,高为h,其内装蓝色液体若干.若如图②放置时,测得液面高为 ;若如图③放置时,测得液面高为 则该玻璃密封容器的容积 圆柱体容积 底面积 高 是 .(结果保留 )
16.如图所示,AB是⊙O的直径,AD、BC是⊙O的两条切线,E、F分别在AD、BC上,EF切⊙O于点G,连接OE、OF、BG、AG,BG与OF相交于点M,AG与OE相交于点N,已知AE=2,BF=8.以下结论:①⊙O的半径为2;②AG∥OF;③BG= ;④四边形OMGN是正方形.其中正确的结论有 (填序号).
三、解答题
17.如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长.
18.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
四、综合题
19.已知, 内接于 ,AD、BD为 的弦,且 .
(1)如图1,求证: ;
(2)如图2,过B作 的切线交AC的延长线于E,求证: ;
(3)如图3,在(2)的条件下,连接CD,若 , , ,求CE的长度.
答案
1.C
2.C
3.B
4.B
5.D
6.D
7.B
8.A
9.D
10.A
11.100
12.15π
13.
14.2
15. a2h
16.②③
17.解:连接OE,
∵OA=OE,∠BAC=40°,
∴∠AOE=100°,
∴ 的长= = ,
连接AD、OD,
∵AB为圆O的直径,
∴∠ADB=90°,又AB=AC,
∴∠BAD= ∠BAC=20°,
∴∠BOD=40°,
∴ 的长= = 。
18.解:由题意得: ,
∴ =6(cm),
∴由勾股定理得:
(cm),
即该圆锥的高为 cm.
19.(1)证明:
∵
∴
∵
∴
∴ ;
(2)证明:连OB、OD,如图,
∵BE为切线
∴
∴ ,
∴
则
,
∴
(3)解:如图,连接 ,
是 的切线,
如图,延长AD交BC的延长线于G,作 于G, 于N, 于Q,延长AB至S,连接ES,使 ,作 于F, 于R,
∵ ,
设 , ,则 ,
∴
∴
∴
∵
∴ ,
又
,
∵ ,设 , ,
,则 ,
,
又
∴
∴ ,
∵
∴在 中, ,
在 中, ,
即
∴
∴ ,设 ,
∵
在 与 中,
∴
∴
解得:
∴
,
∴
∵
∴
∴
∵ ,
∴ 1 / 3
一、单选题
1.已知圆心角度数为60°,半径为30,则这个圆心角所对的弧长为( )
A.20π B.15π C.10π D.5π
2.已知扇形的半径为6,圆心角为10°,则扇形的面积为( )
A. B. C.π D.2π
3.三个正方形方格在扇形中的位置如图所示,点O为扇形的圆心,格点A,B,C分别在扇形的两条半径和弧上,已知每个方格的边长为1,则 的长为( )
A. B. C. D.
4. 如图,直径AB为3的半圆,绕A点逆时针旋转60°,此时点B到了点B′处,则图中阴影部分的面积是( )
A.3π B. C.6π D.24π
5.一个形如圆锥冰淇淋纸筒,其底面直径为6cm,母线长为10cm,围成这样的冰淇淋纸筒所需纸的面积是( )
A.60πcm2 B.15πcm2 C.28πcm2 D.30πcm2
6.如图,在等腰△ABC中,∠BAC=120°,AD是∠BAC的角平分线,且AD=6,以点A为圆心,AD长为半径画弧,交AB于点E,交AC于点F,将阴影部分剪掉,余下扇形AEF,将扇形AEF围成一个圆锥的侧面,AE与AF正好重合,圆锥侧面无重叠,求这个圆锥的高为( )
A.2 B. C.4 D.
7.如图是一个几何体的三视图,根据图中所标数据计算这个几何体的体积为( )
A. B. C. D.
8.一个圆柱体和一个圆锥体的底面周长之比是 ,它们的体积比也是 ,圆柱和圆锥的高的比是( )
A.1:1 B.3:1 C.1:9 D.1:3
9.如图,一圆柱体的底面周长为3πcm,高AB为4cm,BC是上底面的直径.一只蚂蚁从点A出发,沿着圆柱的侧面爬行到点C,爬行的最短路程是( ).
A.3πcm B.5cm
C. cm D. cm
10.如图,⊙O的直径AB=5,弦AC=3,点D是劣弧BC上的动点,CE⊥DC交AD于点E,则OE的最小值是( )
A. B. C.2- D. -1
二、填空题
11.己知弧的长是π,弧的半径为3,则该弧所对的圆心角度数为 °.
12.如图,扇形纸扇完全打开后,外侧两竹条AB,AC夹角为150°,AB的长为18cm,则弧BC的长为 cm.
13.一个扇形的圆心角为 ,面积为 ,则此扇形的半径长为 cm.
14.如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为4cm的等边三角形,点D是母线的中点,一只蚂蚁从点B出发沿圆锥的表面爬行到点D处,则这只蚂蚁爬行的最短距离是 cm.
15.有一个不完整圆柱形玻璃密封容器如图①,测得其底面半径为a,高为h,其内装蓝色液体若干.若如图②放置时,测得液面高为 ;若如图③放置时,测得液面高为 则该玻璃密封容器的容积 圆柱体容积 底面积 高 是 .(结果保留 )
16.如图所示,AB是⊙O的直径,AD、BC是⊙O的两条切线,E、F分别在AD、BC上,EF切⊙O于点G,连接OE、OF、BG、AG,BG与OF相交于点M,AG与OE相交于点N,已知AE=2,BF=8.以下结论:①⊙O的半径为2;②AG∥OF;③BG= ;④四边形OMGN是正方形.其中正确的结论有 (填序号).
三、解答题
17.如图,在△ABC中,AB=AC=8cm,∠BAC=40°,以腰AB为直径作半圆O,分别交BC,AC于点D,E.求 , 的长.
18.如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2 cm,扇形的圆心角θ=120°,求该圆锥的高h的长.
四、综合题
19.已知, 内接于 ,AD、BD为 的弦,且 .
(1)如图1,求证: ;
(2)如图2,过B作 的切线交AC的延长线于E,求证: ;
(3)如图3,在(2)的条件下,连接CD,若 , , ,求CE的长度.
答案
1.C
2.C
3.B
4.B
5.D
6.D
7.B
8.A
9.D
10.A
11.100
12.15π
13.
14.2
15. a2h
16.②③
17.解:连接OE,
∵OA=OE,∠BAC=40°,
∴∠AOE=100°,
∴ 的长= = ,
连接AD、OD,
∵AB为圆O的直径,
∴∠ADB=90°,又AB=AC,
∴∠BAD= ∠BAC=20°,
∴∠BOD=40°,
∴ 的长= = 。
18.解:由题意得: ,
∴ =6(cm),
∴由勾股定理得:
(cm),
即该圆锥的高为 cm.
19.(1)证明:
∵
∴
∵
∴
∴ ;
(2)证明:连OB、OD,如图,
∵BE为切线
∴
∴ ,
∴
则
,
∴
(3)解:如图,连接 ,
是 的切线,
如图,延长AD交BC的延长线于G,作 于G, 于N, 于Q,延长AB至S,连接ES,使 ,作 于F, 于R,
∵ ,
设 , ,则 ,
∴
∴
∴
∵
∴ ,
又
,
∵ ,设 , ,
,则 ,
,
又
∴
∴ ,
∵
∴在 中, ,
在 中, ,
即
∴
∴ ,设 ,
∵
在 与 中,
∴
∴
解得:
∴
,
∴
∵
∴
∴
∵ ,
∴ 1 / 3
