2022年人教版八年级数学下册17.1勾股定理课后练习(Word版含答案)
文档属性
| 名称 | 2022年人教版八年级数学下册17.1勾股定理课后练习(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 220.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览


文档简介
第十七章 勾股定理 17.1 勾股定理 课后练习
一、选择题
1.下列四组数中,是勾股数的是( )
A.5,12,13 B.,, C.1,, D.7,24,26
2.在直角坐标系中,点P(2,﹣3)到原点的距离是( )
A. B. C. D.2
3.如图,在Rt△ABC中,∠BCA=90°,△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,则△ACH的面积是( )
A.2 B.4 C.6 D.9
4.如图,Rt△ABC中,∠ABC=90°,∠CAB的角平分线交BC于M,∠ACB的外角平分线与AM交于点D,与AB的延长线交于点N,过D作DE⊥CN交CB的延长线于点P,交AN于点E,连接CE并延长交PN于点Q,则下列结论: ①∠ADP=45°;②AN=CA+CP;③DC=ED;④NQ﹣CD=PQ;⑤CN=DE+EP,其中正确的结论有( )个.
A.2 B.3 C.4 D.5
5.如图所示,在中,分别以三角形的三条边为边向外作正方形,面积分别记为,,,若,,则的值为( )
A.17 B.20 C.25 D.31
6.如图,四边形ABCD中,∠B=90°,CD=2,AE平分∠BAD,DE平分∠ADC,∠AED=120°,设AB=x,CE=y,则下列式子可以表示线段AD长的是( )
A.x+y+ B.x+y+2 C.x+y+2 D.x+y+
7.如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )
(1)DE平分∠CDA;(2)△EBA≌△EDA;(3)△EBA≌△DCE;(4)AB+CD=AD;(5)AE2+DE2=AD2
A.4个 B.3个 C.2个 D.1个
8.如图,在Rt△ABC中,AB=6,BC=8,AD为∠BAC的平分线,将△ADC沿直线AD翻折得△ADE,则DE的长为( )
A.4 B.5 C.6 D.7
9.如图所示,小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.2m B.2.25m C.2.5m D.3m
10.如图,,一架云梯长为25米,顶端A靠在墙上,此时云梯底端B与墙角C距离为7米,云梯滑动后停在的位置上,测得长为4米,则云梯底端B在水平方向滑动的距离为( )
A.4米 B.6米 C.8米 D.10米
二、填空题
11.△ABO是边长为2的等边三角形,则任意一边上的高长为___.
12.点Q(5,﹣12)到原点的距离是 .
13.已知等腰直角三角形的面积为2,则它的周长为 .(结果保留根号)
14.在Rt△ABC中,∠C=90°,∠A=30°,BC=3,则AC的长为 .(结果保留根号)
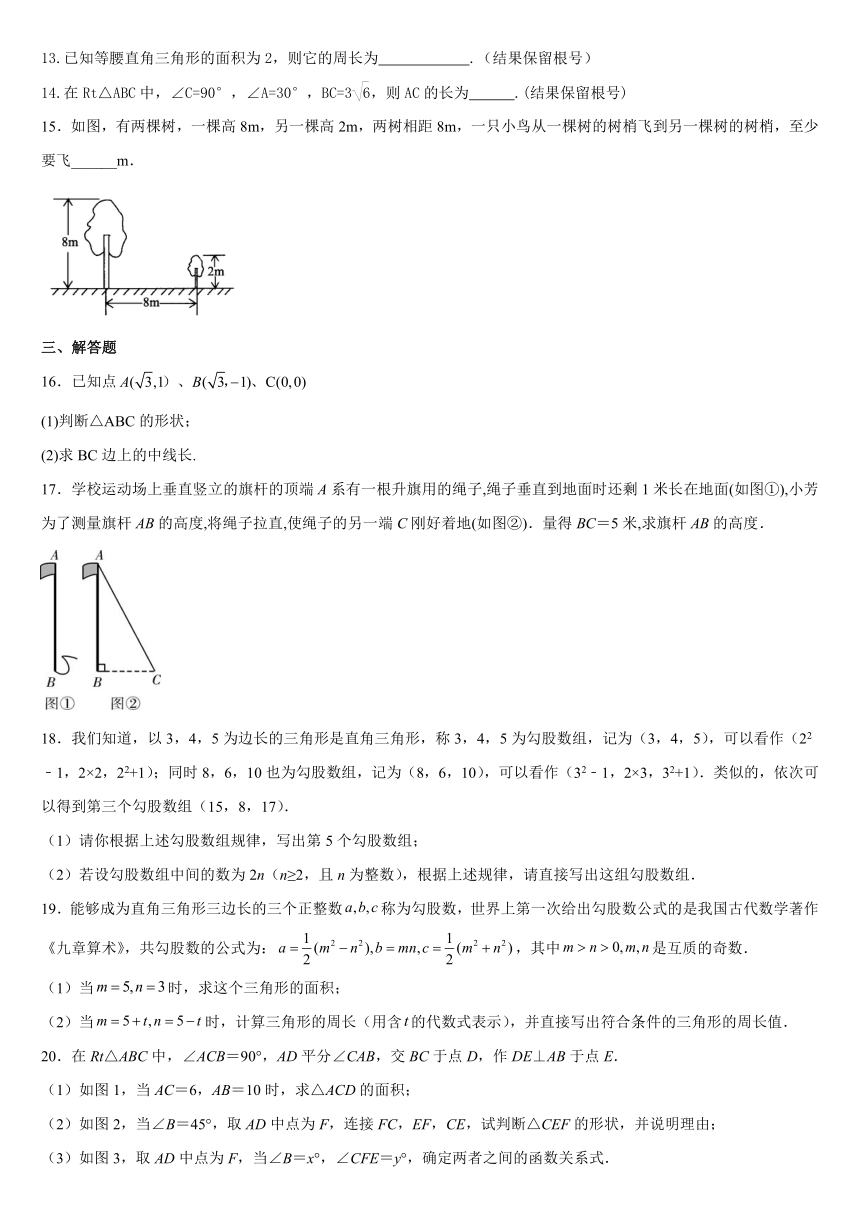
15.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m.
三、解答题
16.已知点
(1)判断△ABC的形状;
(2)求BC边上的中线长.
17.学校运动场上垂直竖立的旗杆的顶端A系有一根升旗用的绳子,绳子垂直到地面时还剩1米长在地面(如图①),小芳为了测量旗杆AB的高度,将绳子拉直,使绳子的另一端C刚好着地(如图②).量得BC=5米,求旗杆AB的高度.
18.我们知道,以3,4,5为边长的三角形是直角三角形,称3,4,5为勾股数组,记为(3,4,5),可以看作(22﹣1,2×2,22+1);同时8,6,10也为勾股数组,记为(8,6,10),可以看作(32﹣1,2×3,32+1).类似的,依次可以得到第三个勾股数组(15,8,17).
(1)请你根据上述勾股数组规律,写出第5个勾股数组;
(2)若设勾股数组中间的数为2n(n≥2,且n为整数),根据上述规律,请直接写出这组勾股数组.
19.能够成为直角三角形三边长的三个正整数称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》,共勾股数的公式为:,其中是互质的奇数.
(1)当时,求这个三角形的面积;
(2)当时,计算三角形的周长(用含的代数式表示),并直接写出符合条件的三角形的周长值.
20.在Rt△ABC中,∠ACB=90°,AD平分∠CAB,交BC于点D,作DE⊥AB于点E.
(1)如图1,当AC=6,AB=10时,求△ACD的面积;
(2)如图2,当∠B=45°,取AD中点为F,连接FC,EF,CE,试判断△CEF的形状,并说明理由;
(3)如图3,取AD中点为F,当∠B=x°,∠CFE=y°,确定两者之间的函数关系式.
21.如图,已知,数轴上点A表示的数为a.
(1)求出数轴上点A所表示的数a.
(2)比较点A所表示的数a与的大小.
(3)求的值.
22.如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米?
【参考答案】
1.A 2.C 3.A 4.B 5.D 6.B 7.B 8.B 9.A 10.C
11.
12.:13.
13.:4+2.
14.:9.
15.10
16.(1)△ABC是等边三角形;(2)BC边上的中线长为.
17.12米
18.(1)(35,12,37);(2)n2﹣1,2n,n2+1
19.(1)三角形的面积为;(2);符合条件的三角形的周长为70.
20.(1)∵∠ACB=90°,AC=6,AB=10,
∴BC===8,
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AD=AE=6,BE=4,
令CD=x,则DE=x,DB=8﹣x,
∵DE2+BE2=BD2,
∴x2+42=(8﹣x)2,
解得x=3,
∴DE=3,
∴S△ACD=AC CD=×6×3=9.
(2)解:△CEF为等腰直角三角形.
∵DE⊥AB,
∴∠AED=90°,
∵∠ACB=90°,F为AD的中点,
∴CF=AF=DF=EF=AD,
∴∠CAF=∠ACF,∠FAE=∠AEF,
∵∠B=45°,AD平分∠CAB,
∴∠CAF=∠EAF=22.5°,
∴∠CFD=∠ACF+∠CAF=2∠CAF=45°,
∠EFD=∠EAF+∠AEF=2∠EAF=45°,
∵∠CFE=∠CFD+∠EFD=2∠CAF+2∠CAF=90°,
∴△CEF为等腰直角三角形.
(3)由(2)知∠CFE=2∠CAF+2∠CAF=2∠CAB=2(90°﹣x),
∴y=2(90﹣x)=180﹣2x.
21.(1)由数轴可知:.
∴数轴上点A所表示的数a为:;
(2)∵,,,
∴,
∴,
即;
(3),,
则
.
22.如图,
由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC= (米),
所以飞机飞行的速度为 (千米/小时)
一、选择题
1.下列四组数中,是勾股数的是( )
A.5,12,13 B.,, C.1,, D.7,24,26
2.在直角坐标系中,点P(2,﹣3)到原点的距离是( )
A. B. C. D.2
3.如图,在Rt△ABC中,∠BCA=90°,△PAB中AB边上的高等于AB的长度,△QBC中BC边上的高等于BC的长度,△HAC中AC边上的高等于AC的长度,且△PAB,△QBC的面积分别是10和8,则△ACH的面积是( )
A.2 B.4 C.6 D.9
4.如图,Rt△ABC中,∠ABC=90°,∠CAB的角平分线交BC于M,∠ACB的外角平分线与AM交于点D,与AB的延长线交于点N,过D作DE⊥CN交CB的延长线于点P,交AN于点E,连接CE并延长交PN于点Q,则下列结论: ①∠ADP=45°;②AN=CA+CP;③DC=ED;④NQ﹣CD=PQ;⑤CN=DE+EP,其中正确的结论有( )个.
A.2 B.3 C.4 D.5
5.如图所示,在中,分别以三角形的三条边为边向外作正方形,面积分别记为,,,若,,则的值为( )
A.17 B.20 C.25 D.31
6.如图,四边形ABCD中,∠B=90°,CD=2,AE平分∠BAD,DE平分∠ADC,∠AED=120°,设AB=x,CE=y,则下列式子可以表示线段AD长的是( )
A.x+y+ B.x+y+2 C.x+y+2 D.x+y+
7.如图所示,∠B=∠C=90°,E是BC的中点,AE平分∠DAB,则下列说法正确的个数是( )
(1)DE平分∠CDA;(2)△EBA≌△EDA;(3)△EBA≌△DCE;(4)AB+CD=AD;(5)AE2+DE2=AD2
A.4个 B.3个 C.2个 D.1个
8.如图,在Rt△ABC中,AB=6,BC=8,AD为∠BAC的平分线,将△ADC沿直线AD翻折得△ADE,则DE的长为( )
A.4 B.5 C.6 D.7
9.如图所示,小明准备测量一段河水的深度,他把一根竹竿竖直插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( )
A.2m B.2.25m C.2.5m D.3m
10.如图,,一架云梯长为25米,顶端A靠在墙上,此时云梯底端B与墙角C距离为7米,云梯滑动后停在的位置上,测得长为4米,则云梯底端B在水平方向滑动的距离为( )
A.4米 B.6米 C.8米 D.10米
二、填空题
11.△ABO是边长为2的等边三角形,则任意一边上的高长为___.
12.点Q(5,﹣12)到原点的距离是 .
13.已知等腰直角三角形的面积为2,则它的周长为 .(结果保留根号)
14.在Rt△ABC中,∠C=90°,∠A=30°,BC=3,则AC的长为 .(结果保留根号)
15.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m.
三、解答题
16.已知点
(1)判断△ABC的形状;
(2)求BC边上的中线长.
17.学校运动场上垂直竖立的旗杆的顶端A系有一根升旗用的绳子,绳子垂直到地面时还剩1米长在地面(如图①),小芳为了测量旗杆AB的高度,将绳子拉直,使绳子的另一端C刚好着地(如图②).量得BC=5米,求旗杆AB的高度.
18.我们知道,以3,4,5为边长的三角形是直角三角形,称3,4,5为勾股数组,记为(3,4,5),可以看作(22﹣1,2×2,22+1);同时8,6,10也为勾股数组,记为(8,6,10),可以看作(32﹣1,2×3,32+1).类似的,依次可以得到第三个勾股数组(15,8,17).
(1)请你根据上述勾股数组规律,写出第5个勾股数组;
(2)若设勾股数组中间的数为2n(n≥2,且n为整数),根据上述规律,请直接写出这组勾股数组.
19.能够成为直角三角形三边长的三个正整数称为勾股数,世界上第一次给出勾股数公式的是我国古代数学著作《九章算术》,共勾股数的公式为:,其中是互质的奇数.
(1)当时,求这个三角形的面积;
(2)当时,计算三角形的周长(用含的代数式表示),并直接写出符合条件的三角形的周长值.
20.在Rt△ABC中,∠ACB=90°,AD平分∠CAB,交BC于点D,作DE⊥AB于点E.
(1)如图1,当AC=6,AB=10时,求△ACD的面积;
(2)如图2,当∠B=45°,取AD中点为F,连接FC,EF,CE,试判断△CEF的形状,并说明理由;
(3)如图3,取AD中点为F,当∠B=x°,∠CFE=y°,确定两者之间的函数关系式.
21.如图,已知,数轴上点A表示的数为a.
(1)求出数轴上点A所表示的数a.
(2)比较点A所表示的数a与的大小.
(3)求的值.
22.如图,飞机在空中水平飞行,某一时刻刚好飞到一男孩子头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米.飞机每小时飞行多少千米?
【参考答案】
1.A 2.C 3.A 4.B 5.D 6.B 7.B 8.B 9.A 10.C
11.
12.:13.
13.:4+2.
14.:9.
15.10
16.(1)△ABC是等边三角形;(2)BC边上的中线长为.
17.12米
18.(1)(35,12,37);(2)n2﹣1,2n,n2+1
19.(1)三角形的面积为;(2);符合条件的三角形的周长为70.
20.(1)∵∠ACB=90°,AC=6,AB=10,
∴BC===8,
∵AD平分∠CAB,DE⊥AB,∠C=90°,
∴CD=ED,∠DEA=∠C=90°,
∵在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AD=AE=6,BE=4,
令CD=x,则DE=x,DB=8﹣x,
∵DE2+BE2=BD2,
∴x2+42=(8﹣x)2,
解得x=3,
∴DE=3,
∴S△ACD=AC CD=×6×3=9.
(2)解:△CEF为等腰直角三角形.
∵DE⊥AB,
∴∠AED=90°,
∵∠ACB=90°,F为AD的中点,
∴CF=AF=DF=EF=AD,
∴∠CAF=∠ACF,∠FAE=∠AEF,
∵∠B=45°,AD平分∠CAB,
∴∠CAF=∠EAF=22.5°,
∴∠CFD=∠ACF+∠CAF=2∠CAF=45°,
∠EFD=∠EAF+∠AEF=2∠EAF=45°,
∵∠CFE=∠CFD+∠EFD=2∠CAF+2∠CAF=90°,
∴△CEF为等腰直角三角形.
(3)由(2)知∠CFE=2∠CAF+2∠CAF=2∠CAB=2(90°﹣x),
∴y=2(90﹣x)=180﹣2x.
21.(1)由数轴可知:.
∴数轴上点A所表示的数a为:;
(2)∵,,,
∴,
∴,
即;
(3),,
则
.
22.如图,
由题意得,AC=4000米,∠C=90°,AB=5000米,由勾股定理得BC= (米),
所以飞机飞行的速度为 (千米/小时)
