2022年人教版八年级数学下册17.1 勾股定理 同步练习(Word版含答案)
文档属性
| 名称 | 2022年人教版八年级数学下册17.1 勾股定理 同步练习(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 23:18:31 | ||
图片预览



文档简介
17.1勾股定理同步练习
一、选择题
1如图,长方形纸片 中,,,将此长方形纸片折叠,使点 与点 重合,点 落在点 的位置,折痕为 ,则 的面积为
A. B. C. D.
2.在平面直角坐标系中,已知点A(1,3)和点B(3,1),点C、D分别是x轴,y轴上的动点,则四边形ABCD的周长最小值为( )
A.5 B.6 C.2+2 D.8
3.如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC,BC为斜边作三个等腰直角△ABD,△ACE,△BCF,图中阴影部分的面积分别记为S1,S2,S3,S4,若已知Rt△ABC的面积,则下列代数式中,一定能求出确切值的代数式是( )
A.S4 B.S1+S4﹣S3 C.S2+S3+S4 D.S1+S2﹣S3
4. 中, 是垂足,与交于,则.
A. B. C. D.
5如图是一个三级台阶,它的每一级的长、宽、高分别为 ,,. 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点 的最短路程为
A. B. C. D.
6.如图,有两棵树,一棵高19米,另一棵高10米,两树相距12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.10米 B.15米 C.16米 D.20米
7.如图,已知钓鱼竿的长为,露在水面上的鱼线长为,某钓鱼者想看看鱼钩上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线为,则的长为( )
A. B. C. D.
8.在△ABC中,∠C=90°,AB=3,则AB2+BC2+AC2的值为( )
A.6 B.9 C.12 D.18
9如图是一个三级台阶,它的每一级的长、宽和高分别是 ,,, 和 是这个台阶的两个相对的端点, 点有一只壁虎,它想到 点去吃可口的食物,请你想一想,这只壁虎从 点出发,沿着台阶面爬到 点,至少需爬
A. B. C. D.
10 为了求出湖两岸 , 两点之间的距离,一个观测者在点 设桩,使 恰好为直角三角形,如图,通过测量,得到 ,,则点 , 的距离是
A. B. C. D.
二、填空题(共5题)
11如图,在 中,,,,点 是 的中点,点 是边 上的一动点,沿 所在直线把 翻折到 的位置, 交 于点 ,若 是直角三角形,则 的长为 .
12.已知:点A的坐标为,点B坐标为,那么点A和点B两点间的距离是______.
13.如图,在数轴上,点O所对应的实数是0,点A所对应的实数是2,过点A作数轴的垂线段,且,连接.以O为圆心,的长为半径画弧,交数轴的负半轴于点C,则点C对应的实数为______.
14.如图,小明想要测量学校旗杆AB的高度,他发现系在旗杆顶端的绳子垂到了地面,从而测得绳子比旗杆长a米,小明将这根绳子拉直,绳子的末端落在地面的点C处,点C距离旗杆底部b米(),则旗杆AB的高度为__________米(用含a,b的代数式表示).
15如图,有一张长方形纸片 ,,,点 为 上一点,将纸片沿 折叠, 的对应边 恰好经过点 ,则线段 的长为 .
三、解答题(共4题)
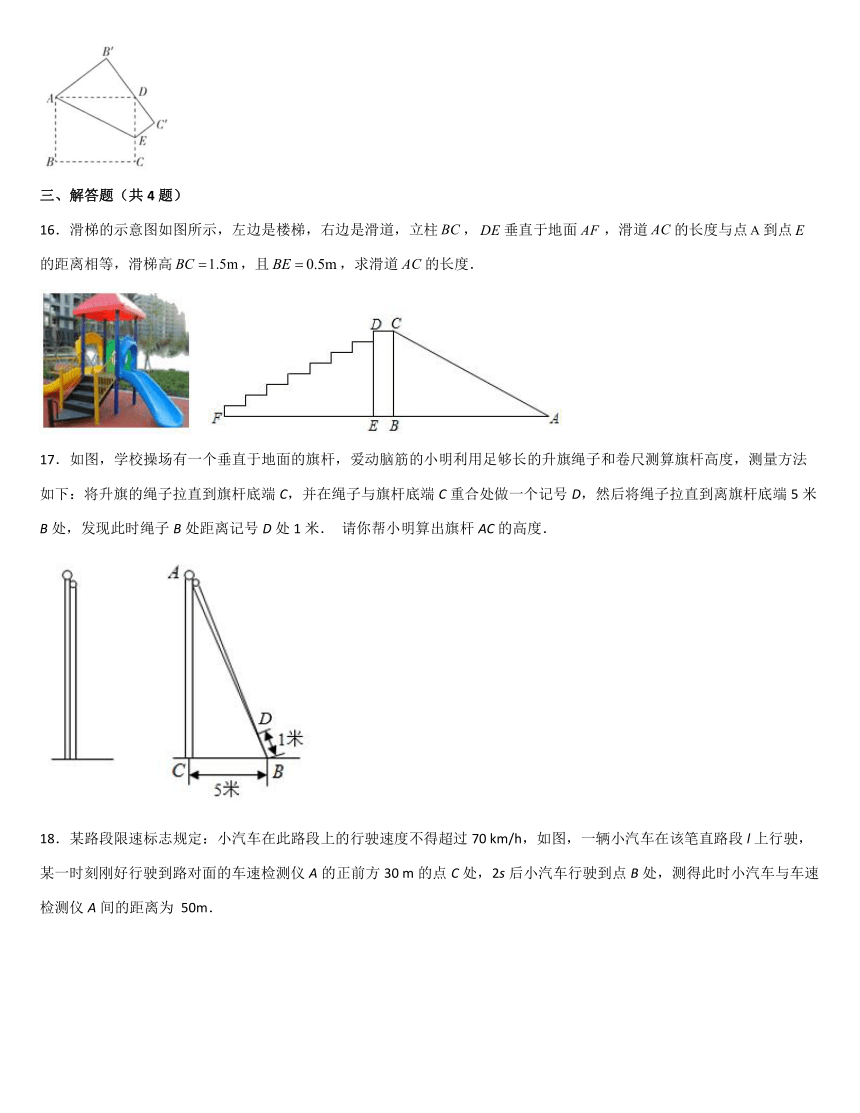
16.滑梯的示意图如图所示,左边是楼梯,右边是滑道,立柱,垂直于地面,滑道的长度与点到点的距离相等,滑梯高,且,求滑道的长度.
17.如图,学校操场有一个垂直于地面的旗杆,爱动脑筋的小明利用足够长的升旗绳子和卷尺测算旗杆高度,测量方法如下:将升旗的绳子拉直到旗杆底端C,并在绳子与旗杆底端C重合处做一个记号D,然后将绳子拉直到离旗杆底端5米B处,发现此时绳子B处距离记号D处1米. 请你帮小明算出旗杆AC的高度.
18.某路段限速标志规定:小汽车在此路段上的行驶速度不得超过70 km/h,如图,一辆小汽车在该笔直路段l上行驶,某一时刻刚好行驶到路对面的车速检测仪A的正前方30 m的点C处,2s后小汽车行驶到点B处,测得此时小汽车与车速检测仪A间的距离为 50m.
(1)求BC的长.
(2)这辆小汽车超速了吗?并说明理由.
19如图,长方形纸片 中,,将纸片折叠,使顶点 落在边 上的 点处,折痕的一端 点在边 上.
(1) 如图 ,当折痕的另一端 在 边上且 时,求 的长;
(2) 如图 ,当折痕的另一端 在 边上且 时,
求证:;
求 的长;
(3) 如图 ,当折痕的另一端 在 边上, 点的对应点 在长方形内部, 到 的距离为 ,且 时,求 的长.
答案
1.A 2.B 3.A 4.A 5.C 6.B 7.B 8.D 9.C 10.C
11. 或
12.5
13.
14.
15.
16.2.5m
17.设旗杆AC的高度为x米,则米.
∵在中,,
∴,即,
解得:.
故旗杆AC的高度为12米.
18.(1)
解:则根据题意可以得到,
根据勾股定理可得:
,
∴BC的长为40m.
(2)
解:∵该小汽车的速度为:,
,
这辆小汽车超速了.
19.
(1) 因为纸片折叠后顶点 落在边 上的 点处,
所以 ,
因为 ,
所以 ,
在 中,,
即 ,
解得 .
(2) 纸片折叠后顶点 落在边 上的 点处.
所以 ,
因为长方形纸片 的边 ,
所以 ,
所以 ,
所以 ;
因为纸片折叠后顶点 落在边 上的 点处,
所以 ,,,
所以 ,
在 中,,
所以 .
(3) 如图 ,设 与 相交于点 ,过点 作 分别交 , 于 ,,过点 作 交 于点 ,连接 ,
因为 与 的距离为 ,
所以 ,,
在 中,,
设 ,
在 中,根据勾股定理可得:,
在 中,根据勾股定理可得:,
在 中,根据勾股定理可得:,
即 ,
解得:,故 ,
所以 ,
设 ,
在 中,根据勾股定理可得:,
因为 ,
即:,
解得:,
所以 .
一、选择题
1如图,长方形纸片 中,,,将此长方形纸片折叠,使点 与点 重合,点 落在点 的位置,折痕为 ,则 的面积为
A. B. C. D.
2.在平面直角坐标系中,已知点A(1,3)和点B(3,1),点C、D分别是x轴,y轴上的动点,则四边形ABCD的周长最小值为( )
A.5 B.6 C.2+2 D.8
3.如图,在Rt△ABC中,∠ACB=90°,分别以AB,AC,BC为斜边作三个等腰直角△ABD,△ACE,△BCF,图中阴影部分的面积分别记为S1,S2,S3,S4,若已知Rt△ABC的面积,则下列代数式中,一定能求出确切值的代数式是( )
A.S4 B.S1+S4﹣S3 C.S2+S3+S4 D.S1+S2﹣S3
4. 中, 是垂足,与交于,则.
A. B. C. D.
5如图是一个三级台阶,它的每一级的长、宽、高分别为 ,,. 和 是这个台阶上两个相对的端点,点 处有一只蚂蚁,想到点 处去吃可口的食物,则蚂蚁沿着台阶面爬行到点 的最短路程为
A. B. C. D.
6.如图,有两棵树,一棵高19米,另一棵高10米,两树相距12米.若一只小鸟从一棵树的树梢飞到另一棵树的树梢,则小鸟至少飞行( )
A.10米 B.15米 C.16米 D.20米
7.如图,已知钓鱼竿的长为,露在水面上的鱼线长为,某钓鱼者想看看鱼钩上的情况,把鱼竿转动到的位置,此时露在水面上的鱼线为,则的长为( )
A. B. C. D.
8.在△ABC中,∠C=90°,AB=3,则AB2+BC2+AC2的值为( )
A.6 B.9 C.12 D.18
9如图是一个三级台阶,它的每一级的长、宽和高分别是 ,,, 和 是这个台阶的两个相对的端点, 点有一只壁虎,它想到 点去吃可口的食物,请你想一想,这只壁虎从 点出发,沿着台阶面爬到 点,至少需爬
A. B. C. D.
10 为了求出湖两岸 , 两点之间的距离,一个观测者在点 设桩,使 恰好为直角三角形,如图,通过测量,得到 ,,则点 , 的距离是
A. B. C. D.
二、填空题(共5题)
11如图,在 中,,,,点 是 的中点,点 是边 上的一动点,沿 所在直线把 翻折到 的位置, 交 于点 ,若 是直角三角形,则 的长为 .
12.已知:点A的坐标为,点B坐标为,那么点A和点B两点间的距离是______.
13.如图,在数轴上,点O所对应的实数是0,点A所对应的实数是2,过点A作数轴的垂线段,且,连接.以O为圆心,的长为半径画弧,交数轴的负半轴于点C,则点C对应的实数为______.
14.如图,小明想要测量学校旗杆AB的高度,他发现系在旗杆顶端的绳子垂到了地面,从而测得绳子比旗杆长a米,小明将这根绳子拉直,绳子的末端落在地面的点C处,点C距离旗杆底部b米(),则旗杆AB的高度为__________米(用含a,b的代数式表示).
15如图,有一张长方形纸片 ,,,点 为 上一点,将纸片沿 折叠, 的对应边 恰好经过点 ,则线段 的长为 .
三、解答题(共4题)
16.滑梯的示意图如图所示,左边是楼梯,右边是滑道,立柱,垂直于地面,滑道的长度与点到点的距离相等,滑梯高,且,求滑道的长度.
17.如图,学校操场有一个垂直于地面的旗杆,爱动脑筋的小明利用足够长的升旗绳子和卷尺测算旗杆高度,测量方法如下:将升旗的绳子拉直到旗杆底端C,并在绳子与旗杆底端C重合处做一个记号D,然后将绳子拉直到离旗杆底端5米B处,发现此时绳子B处距离记号D处1米. 请你帮小明算出旗杆AC的高度.
18.某路段限速标志规定:小汽车在此路段上的行驶速度不得超过70 km/h,如图,一辆小汽车在该笔直路段l上行驶,某一时刻刚好行驶到路对面的车速检测仪A的正前方30 m的点C处,2s后小汽车行驶到点B处,测得此时小汽车与车速检测仪A间的距离为 50m.
(1)求BC的长.
(2)这辆小汽车超速了吗?并说明理由.
19如图,长方形纸片 中,,将纸片折叠,使顶点 落在边 上的 点处,折痕的一端 点在边 上.
(1) 如图 ,当折痕的另一端 在 边上且 时,求 的长;
(2) 如图 ,当折痕的另一端 在 边上且 时,
求证:;
求 的长;
(3) 如图 ,当折痕的另一端 在 边上, 点的对应点 在长方形内部, 到 的距离为 ,且 时,求 的长.
答案
1.A 2.B 3.A 4.A 5.C 6.B 7.B 8.D 9.C 10.C
11. 或
12.5
13.
14.
15.
16.2.5m
17.设旗杆AC的高度为x米,则米.
∵在中,,
∴,即,
解得:.
故旗杆AC的高度为12米.
18.(1)
解:则根据题意可以得到,
根据勾股定理可得:
,
∴BC的长为40m.
(2)
解:∵该小汽车的速度为:,
,
这辆小汽车超速了.
19.
(1) 因为纸片折叠后顶点 落在边 上的 点处,
所以 ,
因为 ,
所以 ,
在 中,,
即 ,
解得 .
(2) 纸片折叠后顶点 落在边 上的 点处.
所以 ,
因为长方形纸片 的边 ,
所以 ,
所以 ,
所以 ;
因为纸片折叠后顶点 落在边 上的 点处,
所以 ,,,
所以 ,
在 中,,
所以 .
(3) 如图 ,设 与 相交于点 ,过点 作 分别交 , 于 ,,过点 作 交 于点 ,连接 ,
因为 与 的距离为 ,
所以 ,,
在 中,,
设 ,
在 中,根据勾股定理可得:,
在 中,根据勾股定理可得:,
在 中,根据勾股定理可得:,
即 ,
解得:,故 ,
所以 ,
设 ,
在 中,根据勾股定理可得:,
因为 ,
即:,
解得:,
所以 .
