2022年人教版七年级数学下册5.3.1平行线的性质与判定专项测试卷(Word版含答案)
文档属性
| 名称 | 2022年人教版七年级数学下册5.3.1平行线的性质与判定专项测试卷(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 889.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 23:18:28 | ||
图片预览




文档简介
5.3.1平行线的性质
一、单选题
1.下列说法:
①在同一平面内,不相交的两条线段叫做平行线;
②过一点,有且只有一条直线平行于已知直线;
③两条平行直线被第三条直线所截,同位角相等;
④同旁内角相等,两直线平行.
正确的个数有( )个.
A.1 B.2 C.3 D.4
2.如图,DC∥EF∥AB,EH∥DB,则图中与∠AHE相等的角有( )
A.3个 B.4个 C.5个 D.6个
3.如图,直线c与直线a、b都相交.若,,则( )
A. B. C. D.
4.如图:AB∥DE,∠B=30°,∠C=110°,∠D的度数为( )
A.115° B.120° C.100° D.80°
5.(2019·山东济南·中考真题)如图,,平分,若,则的度数为( )
A. B. C. D.
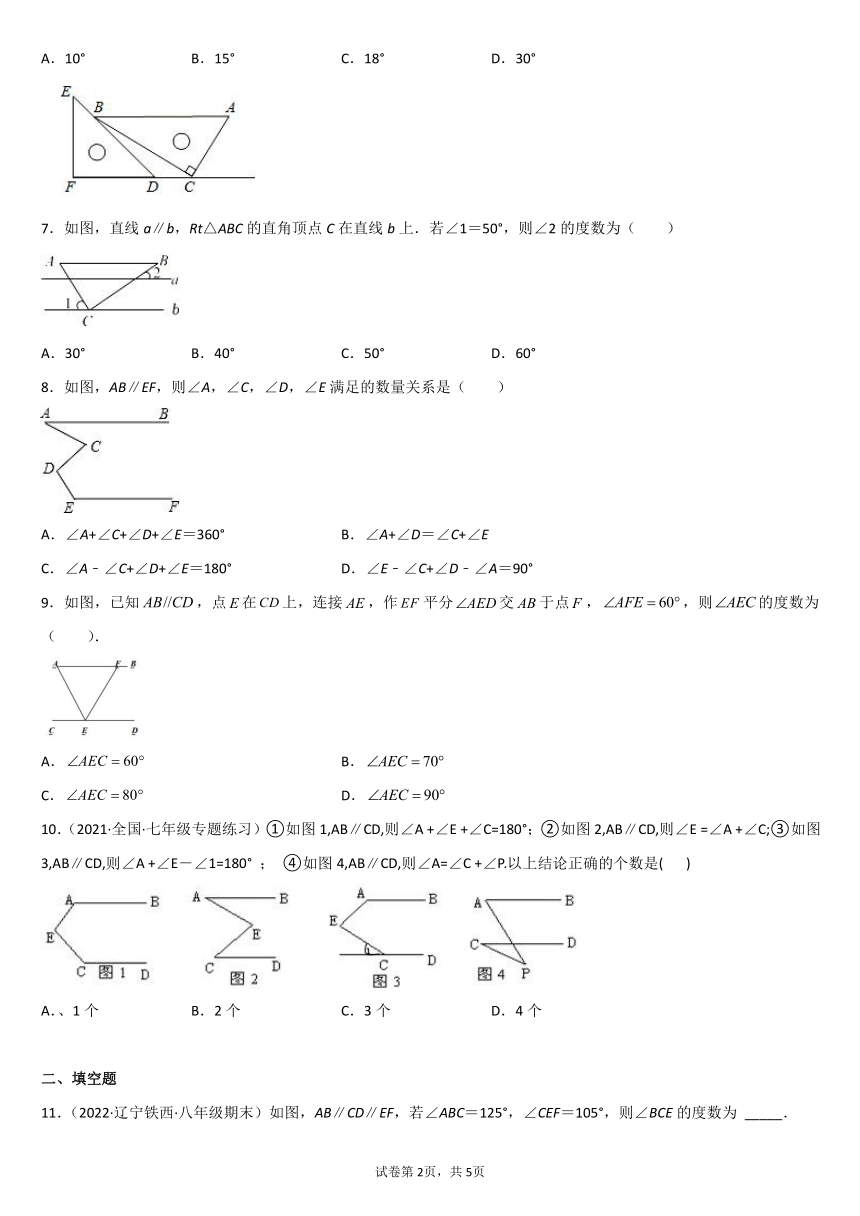
6.一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
7.如图,直线a∥b,Rt△ABC的直角顶点C在直线b上.若∠1=50°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
8.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
9.如图,已知,点在上,连接,作平分交于点,,则的度数为( ).
A. B.
C. D.
10.(2021·全国·七年级专题练习)①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A.、1个 B.2个 C.3个 D.4个
二、填空题
11.(2022·辽宁铁西·八年级期末)如图,AB∥CD∥EF,若∠ABC=125°,∠CEF=105°,则∠BCE的度数为 _____.
12.如图,安装某管道,需经过两次拐弯,若要求拐弯后的管道与拐弯前的管道平行,第一次拐弯处的,那么第二次拐弯处的________.
13.在同一平面内,设a、b、c是三条互相平行的直线,a与b之间的距离为8,b与c之间的距离为3,则a与c之间的距离为 _______.
14.一副直角三角板如图放在直线、之间,且,则图中________度.
15.(2021·全国·七年级专题练习)观察下列图形:已知在第一个图中,可得∠1+∠2=180°,则按照以上规律:_________度.
三、解答题
16.(2022·河南·驻马店市第二初级中学八年级期末)请把下列证明过程及理由补充完整(填在横线上):
已知:如图,BC,AF是直线,AD∥BC,∠1=∠2,∠3=∠4.求证:AB∥CD.
证明:∵AD∥BC(已知),
∴∠3= ( ).
∵∠3=∠4(已知),
∴∠4= ( ).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF( ).
即∠BAF= .
∴∠4=∠BAF.( ).
∴AB∥CD( ).
17.如图所示,点、分别在、上,、均与相交,,,求证:.
18.如图所示,AB//CD,点E为两条平行线外部一点,F为两条平行线内部一点,G、H分别为AB、CD上两点,GB平分∠EGF,HF平分∠EHD,且2∠F与∠E互补,求∠EGF的大小.
19.已知:如图,中,点、分别在、上,交于点, ,.
(1)求证:;
(2)若平分,,求的度数.
20.如图,AB∥DG,∠1+∠2=180°.
(1)试说明:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=142°,求∠B的度数.
21.如图1所示,MN//PQ,∠ABC与MN,PQ分别交于A、C两点
(1)若∠MAB=∠QCB=20°,则B的度数为 度.
(2)在图1分别作∠NAB与∠PCB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②若∠ABC=n°,求∠AFC的度数(用含有n的代数式表示);
(3)如图2所示,直线AE,CD相交于D点,且满足∠BAM=m∠MAE, ∠BCP=m∠DCP,试探究∠CDA与∠ABC的数量关系
22.综合与实践
如图,已知,现将一直角三角形放入图中,其中,交于点E,交于点F.
(1)当所放位置如图①所示时,与的数量关系是___________;
(2)当所放位置如图②所示时,求证:;
(3)在(2)的条件下,若与交于点O,且,,求的度数.
23.(2017·北京东城·七年级期中)已知:直线,点、分别在直线,上,点为平面内一点.
()如图,,,的数量关系是__________.
()利用()的结论解决问题:如图,已知,平分,平分,,求得度数.
()如图,点为上一点,,,交于点,直接写出,,之间的数量关系.(用含的式子表示)
参考答案
1.A 2.C 3.B 4.C 5.B 6.B 7.B 8.C 9.A 10.C
11.50°【详解】
解:∵AB∥CD∥EF,
∴∠BCD=∠ABC=125°,∠CEF+∠ECD=180°,
∴∠ECD=180°-∠CEF=75°,
∴∠BCE=∠BCD-∠ECD=50°,
故答案为:50°.
12.140
13.11或5
14.15
15.(n+1)×180【详解】
解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
∵AB∥CD,
∴AB∥P1E∥P2F∥P3G.
由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°
∴(1)∠1+∠2=180°,
(2)∠1+∠P1+∠2=2×180,
(3)∠1+∠P1+∠P2+∠2=3×180°,
(4)∠1+∠P1+∠P2+∠P3+∠2=4×180°,
∴∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
故答案为:(n+1)×180.
16.【详解】
证明:∵AD∥BC(已知),
∴∠3=∠CAD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠4=∠CAD(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质).
即∠BAF=∠CAD.
∴∠4=∠BAF.(等量代换).
∴AB∥CD(同位角相等,两直线平行).
17.证明:∵,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴.
18.解:过点F作FM∥AB,设AB于EH的交点为N,如图所示:
设,
∵GB平分∠EGF,HF平分∠EHD,
∴,
∵AB//CD,
∴FM∥AB∥CD,
∴,
∴,,
即,,
∵与互补,
∴,
∴,
∴,
∴.
19.解:(1)∵,∠2+∠DFE=180°,
∴∠3=∠DFE,
∴EF//AB,
∴∠ADE=∠1,
又∵,
∴∠ADE=∠B,
∴DE//BC,
(2)∵平分,
∴∠ADE=∠EDC,
∵DE//BC,
∴∠ADE=∠B,
∵
∴∠5+∠ADE+∠EDC==180°,
解得:,
∴∠ADC=2∠B=72°,
∵EF//AB,
∴∠2=∠ADC=180°-108°=72°,
20.(1)∵AB∥DG,
∴∠BAD=∠1,
∵∠1+∠2=180°,
∴∠BAD+∠2=180°.
∵AD∥EF .
(2)∵∠1+∠2=180°且∠2=142°,
∴∠1=38°,
∵DG是∠ADC的平分线,
∴∠CDG=∠1=38°,
∵AB∥DG,
∴∠B=∠CDG=38°.
21.解:(1)作 ,
∵MN//PQ,
∴,
∴ ,
∴ ;
(2)①如图所示,
②过点F作 ,
∴ ,
∴ ,
∵ ,
∴ ,
∵
∴ ,
∴ ,
∵ ,
∴ ;
(3)延长AE交PQ于点G,
设∠MAE=x°,∠DCP=y°,则∠BAM=m∠MAE=mx°,∠BCP=m∠DCP=my°,
∴∠BCQ=180° my°,
由(1)知,∠ABC=mx°+180° my°,
∴y° x°=,
∵MNPQ,
∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP ∠DGC
=y° x°
=,
即m∠CDA+∠ABC=180°.
22.解:(1)如图①,作PH∥AB,
则∠AEM=∠HPM,
∵AB∥CD,PH∥AB,
∴PH∥CD,
∴∠PFD=∠HPN,
∵∠MPN=90°,
∴∠PFD+∠AEM=90°,
故答案为:∠PFD+∠AEM=90°;
(2)猜想:∠PFD ∠AEM=90°;
理由如下:∵AB∥CD,
∴∠PFD+∠BHN=180°,
∵∠BHN=∠PHE,
∴∠PFD+∠PHE=180°,
∵∠P=90°,
∴∠PHE+∠PEB=90°,
∵∠PEB=∠AEM,
∴∠PHE+∠AEM=90°,
∴∠PFD ∠AEM=90°;
(3)如图②,∵∠P=90°,∠PEB=15°,
∴∠PHE=∠P ∠PEB=90° 15°=75°,
∴∠BHF=∠PHE=75°,
∵AB∥CD,
∴∠DFH+∠BHF=180°,
∴∠DFH=180° ∠BHF=105°,
∴∠OFN=∠DFH=105°,
∵∠DON=20°,
∴∠N=180° ∠DON ∠OFN=55°.
23.
【解析】
整体分析:
(1)过作,结合平行公理和平行线的性质即可得到,,的数量关系;(2)直接利用(1)中的结论,结合角平分线的定义及平行线的性质即可;(3)利用平行线的性质和角平分线的定义及角的和差关系建立之间的数量关系.
解:()过作.
∵,
∴,
∴,,
∴
,
即:.
()∵平分,平分,
∴,,
∵,由()结论可知,
∴
,
∴
.
∵,
∴,
又∵
,
∴,
∴.
(),,之间的数量关系是.
∵,,
∴,,
∵,
∴,
∵
EMBED Equation.DSMT4 ,
∴,
∵,
∴,
∴,
∴.
试卷第1页,共3页
试卷第1页,共1页
一、单选题
1.下列说法:
①在同一平面内,不相交的两条线段叫做平行线;
②过一点,有且只有一条直线平行于已知直线;
③两条平行直线被第三条直线所截,同位角相等;
④同旁内角相等,两直线平行.
正确的个数有( )个.
A.1 B.2 C.3 D.4
2.如图,DC∥EF∥AB,EH∥DB,则图中与∠AHE相等的角有( )
A.3个 B.4个 C.5个 D.6个
3.如图,直线c与直线a、b都相交.若,,则( )
A. B. C. D.
4.如图:AB∥DE,∠B=30°,∠C=110°,∠D的度数为( )
A.115° B.120° C.100° D.80°
5.(2019·山东济南·中考真题)如图,,平分,若,则的度数为( )
A. B. C. D.
6.一副直角三角板如图放置,点C在FD的延长线上,AB//CF,∠F=∠ACB=90°,则∠DBC的度数为( )
A.10° B.15° C.18° D.30°
7.如图,直线a∥b,Rt△ABC的直角顶点C在直线b上.若∠1=50°,则∠2的度数为( )
A.30° B.40° C.50° D.60°
8.如图,AB∥EF,则∠A,∠C,∠D,∠E满足的数量关系是( )
A.∠A+∠C+∠D+∠E=360° B.∠A+∠D=∠C+∠E
C.∠A﹣∠C+∠D+∠E=180° D.∠E﹣∠C+∠D﹣∠A=90°
9.如图,已知,点在上,连接,作平分交于点,,则的度数为( ).
A. B.
C. D.
10.(2021·全国·七年级专题练习)①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A.、1个 B.2个 C.3个 D.4个
二、填空题
11.(2022·辽宁铁西·八年级期末)如图,AB∥CD∥EF,若∠ABC=125°,∠CEF=105°,则∠BCE的度数为 _____.
12.如图,安装某管道,需经过两次拐弯,若要求拐弯后的管道与拐弯前的管道平行,第一次拐弯处的,那么第二次拐弯处的________.
13.在同一平面内,设a、b、c是三条互相平行的直线,a与b之间的距离为8,b与c之间的距离为3,则a与c之间的距离为 _______.
14.一副直角三角板如图放在直线、之间,且,则图中________度.
15.(2021·全国·七年级专题练习)观察下列图形:已知在第一个图中,可得∠1+∠2=180°,则按照以上规律:_________度.
三、解答题
16.(2022·河南·驻马店市第二初级中学八年级期末)请把下列证明过程及理由补充完整(填在横线上):
已知:如图,BC,AF是直线,AD∥BC,∠1=∠2,∠3=∠4.求证:AB∥CD.
证明:∵AD∥BC(已知),
∴∠3= ( ).
∵∠3=∠4(已知),
∴∠4= ( ).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF( ).
即∠BAF= .
∴∠4=∠BAF.( ).
∴AB∥CD( ).
17.如图所示,点、分别在、上,、均与相交,,,求证:.
18.如图所示,AB//CD,点E为两条平行线外部一点,F为两条平行线内部一点,G、H分别为AB、CD上两点,GB平分∠EGF,HF平分∠EHD,且2∠F与∠E互补,求∠EGF的大小.
19.已知:如图,中,点、分别在、上,交于点, ,.
(1)求证:;
(2)若平分,,求的度数.
20.如图,AB∥DG,∠1+∠2=180°.
(1)试说明:AD∥EF;
(2)若DG是∠ADC的平分线,∠2=142°,求∠B的度数.
21.如图1所示,MN//PQ,∠ABC与MN,PQ分别交于A、C两点
(1)若∠MAB=∠QCB=20°,则B的度数为 度.
(2)在图1分别作∠NAB与∠PCB的平分线,且两条角平分线交于点F.
①依题意在图1中补全图形;
②若∠ABC=n°,求∠AFC的度数(用含有n的代数式表示);
(3)如图2所示,直线AE,CD相交于D点,且满足∠BAM=m∠MAE, ∠BCP=m∠DCP,试探究∠CDA与∠ABC的数量关系
22.综合与实践
如图,已知,现将一直角三角形放入图中,其中,交于点E,交于点F.
(1)当所放位置如图①所示时,与的数量关系是___________;
(2)当所放位置如图②所示时,求证:;
(3)在(2)的条件下,若与交于点O,且,,求的度数.
23.(2017·北京东城·七年级期中)已知:直线,点、分别在直线,上,点为平面内一点.
()如图,,,的数量关系是__________.
()利用()的结论解决问题:如图,已知,平分,平分,,求得度数.
()如图,点为上一点,,,交于点,直接写出,,之间的数量关系.(用含的式子表示)
参考答案
1.A 2.C 3.B 4.C 5.B 6.B 7.B 8.C 9.A 10.C
11.50°【详解】
解:∵AB∥CD∥EF,
∴∠BCD=∠ABC=125°,∠CEF+∠ECD=180°,
∴∠ECD=180°-∠CEF=75°,
∴∠BCE=∠BCD-∠ECD=50°,
故答案为:50°.
12.140
13.11或5
14.15
15.(n+1)×180【详解】
解:如图,分别过P1、P2、P3作直线AB的平行线P1E,P2F,P3G,
∵AB∥CD,
∴AB∥P1E∥P2F∥P3G.
由平行线的性质可得出:∠1+∠3=180°,∠5+∠6=180°,∠7+∠8=180°,∠4+∠2=180°
∴(1)∠1+∠2=180°,
(2)∠1+∠P1+∠2=2×180,
(3)∠1+∠P1+∠P2+∠2=3×180°,
(4)∠1+∠P1+∠P2+∠P3+∠2=4×180°,
∴∠1+∠2+∠P1+…+∠Pn=(n+1)×180°.
故答案为:(n+1)×180.
16.【详解】
证明:∵AD∥BC(已知),
∴∠3=∠CAD(两直线平行,内错角相等).
∵∠3=∠4(已知),
∴∠4=∠CAD(等量代换).
∵∠1=∠2(已知),
∴∠1+∠CAF=∠2+∠CAF(等式的性质).
即∠BAF=∠CAD.
∴∠4=∠BAF.(等量代换).
∴AB∥CD(同位角相等,两直线平行).
17.证明:∵,
∴,
∴,
又∵,
∴,
∴,
∴,
∵,
∴.
18.解:过点F作FM∥AB,设AB于EH的交点为N,如图所示:
设,
∵GB平分∠EGF,HF平分∠EHD,
∴,
∵AB//CD,
∴FM∥AB∥CD,
∴,
∴,,
即,,
∵与互补,
∴,
∴,
∴,
∴.
19.解:(1)∵,∠2+∠DFE=180°,
∴∠3=∠DFE,
∴EF//AB,
∴∠ADE=∠1,
又∵,
∴∠ADE=∠B,
∴DE//BC,
(2)∵平分,
∴∠ADE=∠EDC,
∵DE//BC,
∴∠ADE=∠B,
∵
∴∠5+∠ADE+∠EDC==180°,
解得:,
∴∠ADC=2∠B=72°,
∵EF//AB,
∴∠2=∠ADC=180°-108°=72°,
20.(1)∵AB∥DG,
∴∠BAD=∠1,
∵∠1+∠2=180°,
∴∠BAD+∠2=180°.
∵AD∥EF .
(2)∵∠1+∠2=180°且∠2=142°,
∴∠1=38°,
∵DG是∠ADC的平分线,
∴∠CDG=∠1=38°,
∵AB∥DG,
∴∠B=∠CDG=38°.
21.解:(1)作 ,
∵MN//PQ,
∴,
∴ ,
∴ ;
(2)①如图所示,
②过点F作 ,
∴ ,
∴ ,
∵ ,
∴ ,
∵
∴ ,
∴ ,
∵ ,
∴ ;
(3)延长AE交PQ于点G,
设∠MAE=x°,∠DCP=y°,则∠BAM=m∠MAE=mx°,∠BCP=m∠DCP=my°,
∴∠BCQ=180° my°,
由(1)知,∠ABC=mx°+180° my°,
∴y° x°=,
∵MNPQ,
∴∠MAE=∠DGP=x°,
则∠CDA=∠DCP ∠DGC
=y° x°
=,
即m∠CDA+∠ABC=180°.
22.解:(1)如图①,作PH∥AB,
则∠AEM=∠HPM,
∵AB∥CD,PH∥AB,
∴PH∥CD,
∴∠PFD=∠HPN,
∵∠MPN=90°,
∴∠PFD+∠AEM=90°,
故答案为:∠PFD+∠AEM=90°;
(2)猜想:∠PFD ∠AEM=90°;
理由如下:∵AB∥CD,
∴∠PFD+∠BHN=180°,
∵∠BHN=∠PHE,
∴∠PFD+∠PHE=180°,
∵∠P=90°,
∴∠PHE+∠PEB=90°,
∵∠PEB=∠AEM,
∴∠PHE+∠AEM=90°,
∴∠PFD ∠AEM=90°;
(3)如图②,∵∠P=90°,∠PEB=15°,
∴∠PHE=∠P ∠PEB=90° 15°=75°,
∴∠BHF=∠PHE=75°,
∵AB∥CD,
∴∠DFH+∠BHF=180°,
∴∠DFH=180° ∠BHF=105°,
∴∠OFN=∠DFH=105°,
∵∠DON=20°,
∴∠N=180° ∠DON ∠OFN=55°.
23.
【解析】
整体分析:
(1)过作,结合平行公理和平行线的性质即可得到,,的数量关系;(2)直接利用(1)中的结论,结合角平分线的定义及平行线的性质即可;(3)利用平行线的性质和角平分线的定义及角的和差关系建立之间的数量关系.
解:()过作.
∵,
∴,
∴,,
∴
,
即:.
()∵平分,平分,
∴,,
∵,由()结论可知,
∴
,
∴
.
∵,
∴,
又∵
,
∴,
∴.
(),,之间的数量关系是.
∵,,
∴,,
∵,
∴,
∵
EMBED Equation.DSMT4 ,
∴,
∵,
∴,
∴,
∴.
试卷第1页,共3页
试卷第1页,共1页
