2022年人教版七年级数学下册5.3.1平行线的性质提高练习(Word版含答案)
文档属性
| 名称 | 2022年人教版七年级数学下册5.3.1平行线的性质提高练习(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 348.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 00:00:00 | ||
图片预览



文档简介
5.3.1平行线的性质
一、单选题
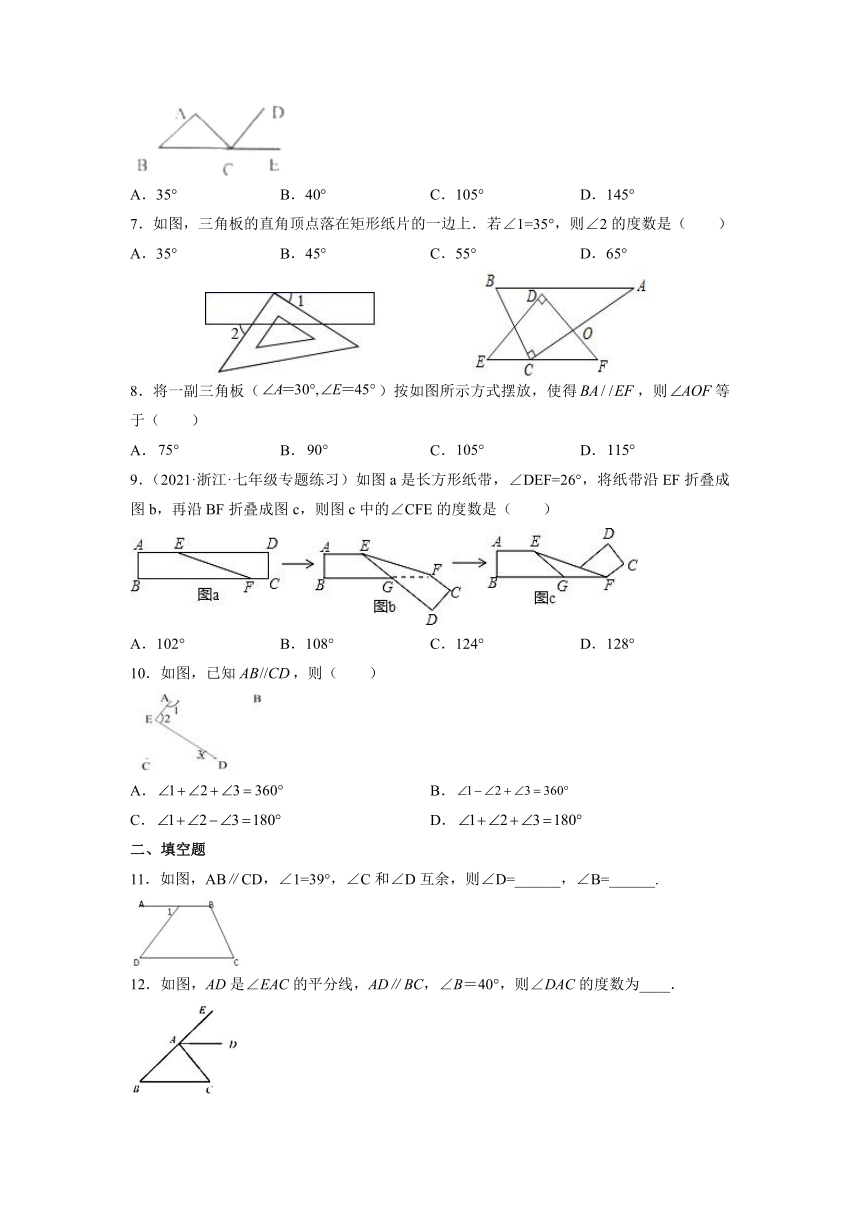
1.如图,a∥b,∠1=120°,则∠2等于( )
A.30° B.90° C.60° D.50°
2.如图,已知∠1=50°,要使a∥b,那么∠2等于( )
A.40° B.130° C.50° D.120°
3.为了加固房屋,要在屋架上加一根横梁DE,使得DEBC,如果,则的度数是( )
A.149° B.159° C.31° D.62°
4.如图,已知∠1 = 40°,∠2=40°,∠3 = 140°,则∠4的度数等于( )
A.40° B.36° C.44° D.100°
5.如图,下列四个选项中不能判断AD∥BC的是( )
A. B.
C. D.
6.如图,已知、、在同一直线上,且,若,,则为( )
A.35° B.40° C.105° D.145°
7.如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.65°
第7题图 第8题图
8.将一副三角板()按如图所示方式摆放,使得,则等于( )
A. B. C. D.
9.(2021·浙江·七年级专题练习)如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
10.如图,已知,则( )
A. B.
C. D.
二、填空题
11.如图,AB∥CD,∠1=39°,∠C和∠D互余,则∠D=______,∠B=______.
12.如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为____.
13.如图,在四边形ABCD中,AB∥CD,AD∥BC,点F在BC的延长线上,CE平分∠DCF交AD的延长线于点E,已知∠E=35°,则∠A=___.
14.如图,已知直线l1∥l2,∠A=125°,∠B=85°,且∠1比∠2大4°,那么∠1=______.
15.如图,已知直线AB,CD被直线AC所截,ABCD,E是平面内任意一点点E不在直线AB,CD,AC上,设,,下列各式:①,②,③,④,则的度数可能是_______(填写序号)
三、解答题
16.如图,已知直线AB∥CD,E是直线CD上一点,过点E作EF⊥AE,垂足为E,交AB于点G,若,求的度数.
17. 如图,AD∥EF,AB∥DG.说明∠1=∠2的理由.
18. 如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
19. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
20. 如图,E为AC上一点,EF∥AB交AF于点F,且∠EAF=∠EFA.试说明:∠BAC =2∠1.
21.如图,AB//CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数(用含n的代数式表示);
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
22.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°,
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.
参考答案
1.C 2.C 3.A 4.A 5.D 6.D 7.C 8.A 9.A 10.C
11.39° 129°
12.40°
13.110 度
14.
15.①②③④
16.
17. 解:∵AD∥EF(已知),
∴∠1=∠BAD(两直线平行,同位角相等).
∵AB∥DG(已知),
∴∠BAD=∠2(两直线平行,内错角相等),
∴∠1=∠2(等量代换).
18. 解:∵EF∥BC,∴∠BAF=180°-∠B=100°.∵AC平分∠BAF,∴∠CAF=∠BAF=50°,∵EF∥BC,∴∠C=∠CAF=50°.
19. 解:∵∠AEC=42°,∴∠AED=180°-∠AEC=138°,∵EF平分∠AED,∴∠DEF=∠AED=69°,又∵AB∥CD,∴∠AFE=∠DEF=69°.
20. 解:∵EF∥AB,∴∠1=∠FAB(两直线平行,同位角相等).由对顶角相等,得∠1=∠EFA,∵∠EAF=∠EFA,∴∠EAF=∠1.∴∠BAC=∠EAF+∠FAB=2∠1.
21.(1)如图1,过点作.
∵,
∴,
∴.
∵平分平分,,
∴.
∵,
∴,
∴.
(2)的度数改变.
画出的图形如图2,过点作.
∵平分,平分,,
∴ .
∵,
∴,
∴.
∵,
∴,
∴,
∴.
22.(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD
(2)∠BAE+∠MCD=90°;理由如下:
如图,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠AEC=∠AEF+∠FEC=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD=∠MCD,
∴∠BAE+∠MCD=90°.
(3)如图,过点C作CM//PQ,
∴∠PQC=∠MCN,∠QPC=∠PCM,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠PCQ+∠PCM+∠MCN=180°,
∴∠QPC+∠PQC+∠PCQ=180°,
∴∠BAC=∠PQC+∠QPC.
一、单选题
1.如图,a∥b,∠1=120°,则∠2等于( )
A.30° B.90° C.60° D.50°
2.如图,已知∠1=50°,要使a∥b,那么∠2等于( )
A.40° B.130° C.50° D.120°
3.为了加固房屋,要在屋架上加一根横梁DE,使得DEBC,如果,则的度数是( )
A.149° B.159° C.31° D.62°
4.如图,已知∠1 = 40°,∠2=40°,∠3 = 140°,则∠4的度数等于( )
A.40° B.36° C.44° D.100°
5.如图,下列四个选项中不能判断AD∥BC的是( )
A. B.
C. D.
6.如图,已知、、在同一直线上,且,若,,则为( )
A.35° B.40° C.105° D.145°
7.如图,三角板的直角顶点落在矩形纸片的一边上.若∠1=35°,则∠2的度数是( )
A.35° B.45° C.55° D.65°
第7题图 第8题图
8.将一副三角板()按如图所示方式摆放,使得,则等于( )
A. B. C. D.
9.(2021·浙江·七年级专题练习)如图a是长方形纸带,∠DEF=26°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是( )
A.102° B.108° C.124° D.128°
10.如图,已知,则( )
A. B.
C. D.
二、填空题
11.如图,AB∥CD,∠1=39°,∠C和∠D互余,则∠D=______,∠B=______.
12.如图,AD是∠EAC的平分线,AD∥BC,∠B=40°,则∠DAC的度数为____.
13.如图,在四边形ABCD中,AB∥CD,AD∥BC,点F在BC的延长线上,CE平分∠DCF交AD的延长线于点E,已知∠E=35°,则∠A=___.
14.如图,已知直线l1∥l2,∠A=125°,∠B=85°,且∠1比∠2大4°,那么∠1=______.
15.如图,已知直线AB,CD被直线AC所截,ABCD,E是平面内任意一点点E不在直线AB,CD,AC上,设,,下列各式:①,②,③,④,则的度数可能是_______(填写序号)
三、解答题
16.如图,已知直线AB∥CD,E是直线CD上一点,过点E作EF⊥AE,垂足为E,交AB于点G,若,求的度数.
17. 如图,AD∥EF,AB∥DG.说明∠1=∠2的理由.
18. 如图,EF∥BC,AC平分∠BAF,∠B=80°.求∠C的度数.
19. 如图,AB∥CD,点E是CD上一点,∠AEC=42°,EF平分∠AED交AB于点F,求∠AFE的度数.
20. 如图,E为AC上一点,EF∥AB交AF于点F,且∠EAF=∠EFA.试说明:∠BAC =2∠1.
21.如图,AB//CD,点C在点D的右侧,∠ABC,∠ADC的平分线交于点E(不与B,D点重合),∠ADC=70°.设∠BED=n°.
(1)若点B在点A的左侧,求∠ABC的度数(用含n的代数式表示);
(2)将(1)中的线段BC沿DC方向平移,当点B移动到点A右侧时,请画出图形并判断∠ABC的度数是否改变.若改变,请求出∠ABC的度数(用含n的代数式表示);若不变,请说明理由.
22.如图1,CE平分∠ACD,AE平分∠BAC,∠EAC+∠ACE=90°,
(1)请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠E=90°且AB与CD的位置关系保持不变,移动直角顶点E,使∠MCE=∠ECD,当直角顶点E点移动时,问∠BAE与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,P为线段AC上一定点,点Q为直线CD上一动点且AB与CD的位置关系保持不变,当点Q在射线CD上运动时(点C除外)∠CPQ+∠CQP与∠BAC有何数量关系?猜想结论并说明理由.
参考答案
1.C 2.C 3.A 4.A 5.D 6.D 7.C 8.A 9.A 10.C
11.39° 129°
12.40°
13.110 度
14.
15.①②③④
16.
17. 解:∵AD∥EF(已知),
∴∠1=∠BAD(两直线平行,同位角相等).
∵AB∥DG(已知),
∴∠BAD=∠2(两直线平行,内错角相等),
∴∠1=∠2(等量代换).
18. 解:∵EF∥BC,∴∠BAF=180°-∠B=100°.∵AC平分∠BAF,∴∠CAF=∠BAF=50°,∵EF∥BC,∴∠C=∠CAF=50°.
19. 解:∵∠AEC=42°,∴∠AED=180°-∠AEC=138°,∵EF平分∠AED,∴∠DEF=∠AED=69°,又∵AB∥CD,∴∠AFE=∠DEF=69°.
20. 解:∵EF∥AB,∴∠1=∠FAB(两直线平行,同位角相等).由对顶角相等,得∠1=∠EFA,∵∠EAF=∠EFA,∴∠EAF=∠1.∴∠BAC=∠EAF+∠FAB=2∠1.
21.(1)如图1,过点作.
∵,
∴,
∴.
∵平分平分,,
∴.
∵,
∴,
∴.
(2)的度数改变.
画出的图形如图2,过点作.
∵平分,平分,,
∴ .
∵,
∴,
∴.
∵,
∴,
∴,
∴.
22.(1)∵CE平分∠ACD,AE平分∠BAC,
∴∠BAC=2∠EAC,∠ACD=2∠ACE,
∵∠EAC+∠ACE=90°,
∴∠BAC+∠ACD=180°,
∴AB∥CD
(2)∠BAE+∠MCD=90°;理由如下:
如图,过E作EF∥AB,
∵AB∥CD,
∴EF∥AB∥CD,
∴∠BAE=∠AEF,∠FEC=∠DCE,
∵∠AEC=∠AEF+∠FEC=90°,
∴∠BAE+∠ECD=90°,
∵∠MCE=∠ECD=∠MCD,
∴∠BAE+∠MCD=90°.
(3)如图,过点C作CM//PQ,
∴∠PQC=∠MCN,∠QPC=∠PCM,
∵AB∥CD,
∴∠BAC+∠ACD=180°,
∵∠PCQ+∠PCM+∠MCN=180°,
∴∠QPC+∠PQC+∠PCQ=180°,
∴∠BAC=∠PQC+∠QPC.
