2022年人教版八年级数学下册17.1 勾股定理 课时练习(Word版含答案)
文档属性
| 名称 | 2022年人教版八年级数学下册17.1 勾股定理 课时练习(Word版含答案) | 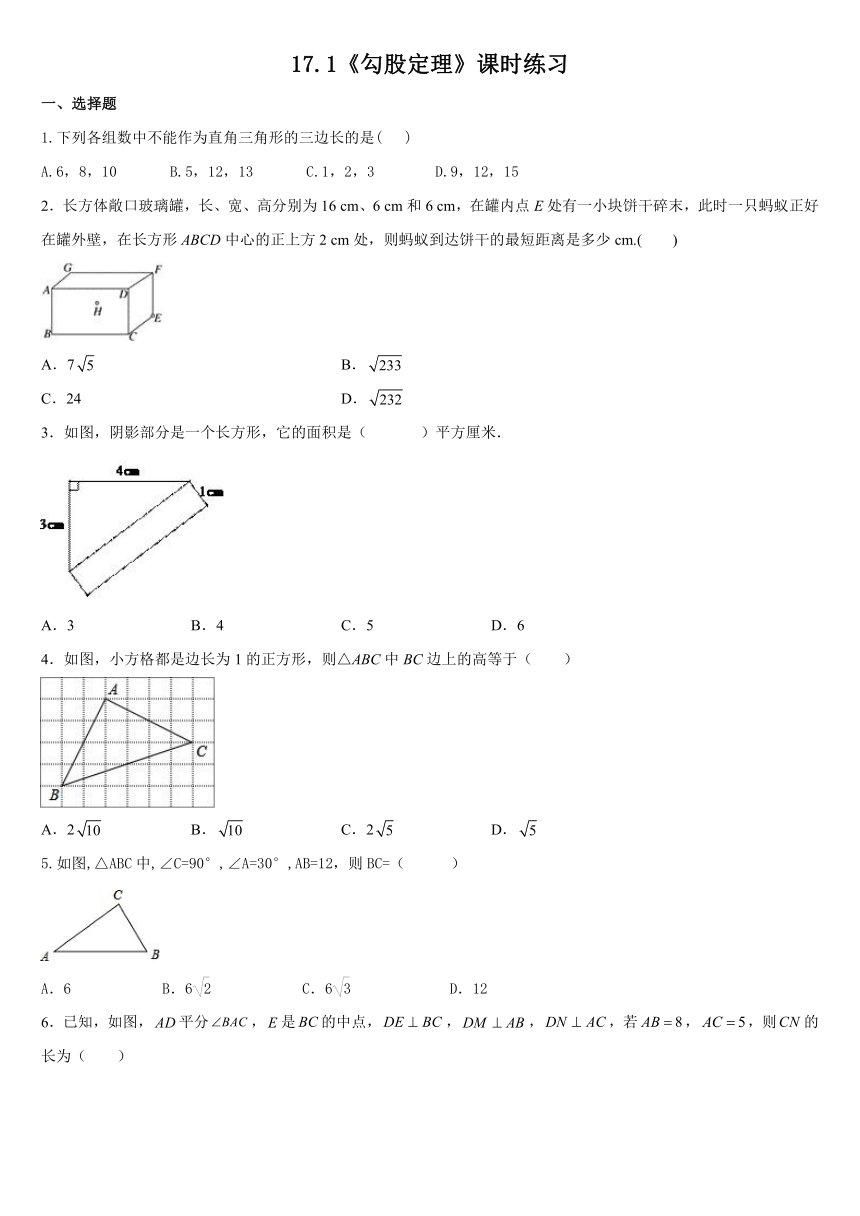 | |
| 格式 | doc | ||
| 文件大小 | 292.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-02-08 23:21:13 | ||
图片预览


文档简介
17.1《勾股定理》课时练习
一、选择题
1.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.5,12,13 C.1,2,3 D.9,12,15
2.长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
A.7 B.
C.24 D.
3.如图,阴影部分是一个长方形,它的面积是( )平方厘米.
A.3 B.4 C.5 D.6
4.如图,小方格都是边长为1的正方形,则△ABC中BC边上的高等于( )
A.2 B. C.2 D.
5.如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
A.6 B.6 C.6 D.12
6.已知,如图,平分,是的中点,,,,若,,则的长为( )
A.1 B. C.2 D.3
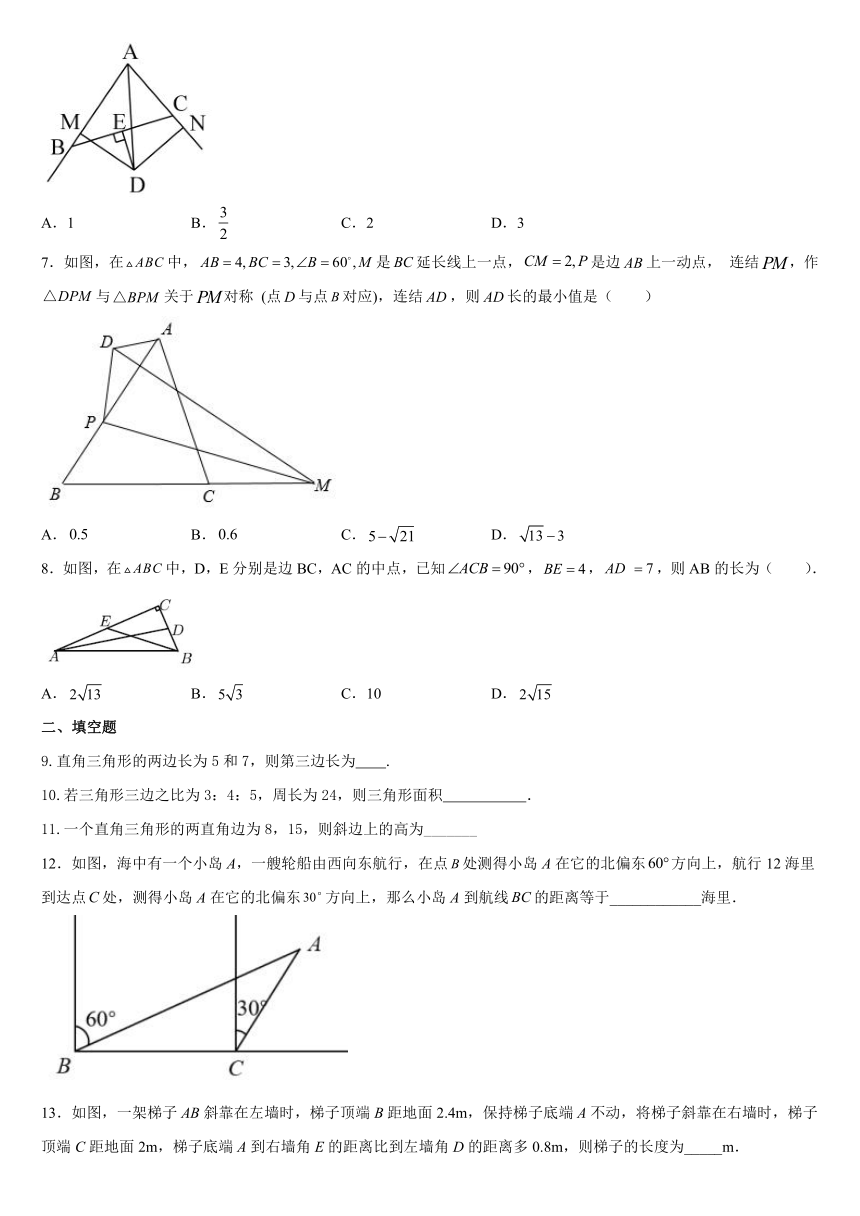
7.如图,在中,是延长线上一点,是边上一动点, 连结,作与关于对称 (点与点对应),连结,则长的最小值是( )
A. B. C. D.
8.如图,在中,D,E分别是边BC,AC的中点,已知,,,则AB的长为( ).
A. B. C.10 D.
二、填空题
9.直角三角形的两边长为5和7,则第三边长为 .
10.若三角形三边之比为3:4:5,周长为24,则三角形面积 .
11.一个直角三角形的两直角边为8,15,则斜边上的高为_______
12.如图,海中有一个小岛A,一艘轮船由西向东航行,在点处测得小岛A在它的北偏东方向上,航行12海里到达点处,测得小岛A在它的北偏东方向上,那么小岛A到航线的距离等于____________海里.
13.如图,一架梯子AB斜靠在左墙时,梯子顶端B距地面2.4m,保持梯子底端A不动,将梯子斜靠在右墙时,梯子顶端C距地面2m,梯子底端A到右墙角E的距离比到左墙角D的距离多0.8m,则梯子的长度为_____m.
14.在△ABC中,∠C=90°,AC=BC=1,将△ABC沿射线AB翻折,得到△ABD,再将AC沿射线AB平移,得到EF,连接DE、DF,则△DEF周长的最小值是__.
三、解答题
15.能够成为直角三角形边长的三个正整数,我们称之为一组勾股数,观察表格所给出的三个数a,b,c,a<b<c.
(1)试找出它们的共同点,并证明你的结论;
(2)写出当a=17时,b,c的值.
16如图,为修建高速铁路需凿通隧道 AC,测得 ,,,若每天可凿隧道 0.3m,需要多少天才能把隧道 AC 凿通?
17如图,在一次数学课外活动中,小明同学在点 P 处测得教学楼 A 位于北偏东 方向,办公楼 B 位于南偏东 方向.小明沿正东方向前进 60 米到达 C 处,此时测得教学楼 A 恰好位于正北方向,办公楼 B 正好位于正南方向.求教学楼 A 与办公楼 B 之间的距离.
18如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算出两圆孔的中心点 A 和点 M 之间的距离.
参考答案
1.C 2.B 3.C 4.B 5.A 6.B 7.C 8.A
9.答案为:2或
10.答案为:24;
11.答案为:
12.
13.##
14.
15.解:(1)以上各组数的共同点可以从以下方面分析:
①以上各组数均满足a2+b2=c2;
②最小的数(a)是奇数,其余的两个数是连续的正整数;
③最小奇数的平方等于另两个连续整数的和,
如32=9=4+5,52=25=12+13,72=49=24+25,92=81=40+41…
由以上特点我们可猜想并证明这样一个结论:
设m为大于1的奇数,将m2拆分为两个连续的整数之和,即m2=n+(n+1),
则m,n,n+1就构成一组简单的勾股数,
证明:∵m2=n+(n+1)(m为大于1的奇数),
∴m2+n2=2n+1+n2=(n+1)2,
∴m,n,(n+1)是一组勾股数;
(2)运用以上结论,当a=17时,
∵172=289=144+145,
∴b=144,c=145.
16. ,
为直角三角形,
,,
,
(天).
答:需要 天才能将隧道 凿通.
17由题意可知:
,,.
在 中,
,,
.
在 中,
,,
.
由勾股定理,,即 ,解得 .
米.
18
一、选择题
1.下列各组数中不能作为直角三角形的三边长的是( )
A.6,8,10 B.5,12,13 C.1,2,3 D.9,12,15
2.长方体敞口玻璃罐,长、宽、高分别为16 cm、6 cm和6 cm,在罐内点E处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形ABCD中心的正上方2 cm处,则蚂蚁到达饼干的最短距离是多少cm.( )
A.7 B.
C.24 D.
3.如图,阴影部分是一个长方形,它的面积是( )平方厘米.
A.3 B.4 C.5 D.6
4.如图,小方格都是边长为1的正方形,则△ABC中BC边上的高等于( )
A.2 B. C.2 D.
5.如图,△ABC中,∠C=90°,∠A=30°,AB=12,则BC=( )
A.6 B.6 C.6 D.12
6.已知,如图,平分,是的中点,,,,若,,则的长为( )
A.1 B. C.2 D.3
7.如图,在中,是延长线上一点,是边上一动点, 连结,作与关于对称 (点与点对应),连结,则长的最小值是( )
A. B. C. D.
8.如图,在中,D,E分别是边BC,AC的中点,已知,,,则AB的长为( ).
A. B. C.10 D.
二、填空题
9.直角三角形的两边长为5和7,则第三边长为 .
10.若三角形三边之比为3:4:5,周长为24,则三角形面积 .
11.一个直角三角形的两直角边为8,15,则斜边上的高为_______
12.如图,海中有一个小岛A,一艘轮船由西向东航行,在点处测得小岛A在它的北偏东方向上,航行12海里到达点处,测得小岛A在它的北偏东方向上,那么小岛A到航线的距离等于____________海里.
13.如图,一架梯子AB斜靠在左墙时,梯子顶端B距地面2.4m,保持梯子底端A不动,将梯子斜靠在右墙时,梯子顶端C距地面2m,梯子底端A到右墙角E的距离比到左墙角D的距离多0.8m,则梯子的长度为_____m.
14.在△ABC中,∠C=90°,AC=BC=1,将△ABC沿射线AB翻折,得到△ABD,再将AC沿射线AB平移,得到EF,连接DE、DF,则△DEF周长的最小值是__.
三、解答题
15.能够成为直角三角形边长的三个正整数,我们称之为一组勾股数,观察表格所给出的三个数a,b,c,a<b<c.
(1)试找出它们的共同点,并证明你的结论;
(2)写出当a=17时,b,c的值.
16如图,为修建高速铁路需凿通隧道 AC,测得 ,,,若每天可凿隧道 0.3m,需要多少天才能把隧道 AC 凿通?
17如图,在一次数学课外活动中,小明同学在点 P 处测得教学楼 A 位于北偏东 方向,办公楼 B 位于南偏东 方向.小明沿正东方向前进 60 米到达 C 处,此时测得教学楼 A 恰好位于正北方向,办公楼 B 正好位于正南方向.求教学楼 A 与办公楼 B 之间的距离.
18如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位:mm),计算出两圆孔的中心点 A 和点 M 之间的距离.
参考答案
1.C 2.B 3.C 4.B 5.A 6.B 7.C 8.A
9.答案为:2或
10.答案为:24;
11.答案为:
12.
13.##
14.
15.解:(1)以上各组数的共同点可以从以下方面分析:
①以上各组数均满足a2+b2=c2;
②最小的数(a)是奇数,其余的两个数是连续的正整数;
③最小奇数的平方等于另两个连续整数的和,
如32=9=4+5,52=25=12+13,72=49=24+25,92=81=40+41…
由以上特点我们可猜想并证明这样一个结论:
设m为大于1的奇数,将m2拆分为两个连续的整数之和,即m2=n+(n+1),
则m,n,n+1就构成一组简单的勾股数,
证明:∵m2=n+(n+1)(m为大于1的奇数),
∴m2+n2=2n+1+n2=(n+1)2,
∴m,n,(n+1)是一组勾股数;
(2)运用以上结论,当a=17时,
∵172=289=144+145,
∴b=144,c=145.
16. ,
为直角三角形,
,,
,
(天).
答:需要 天才能将隧道 凿通.
17由题意可知:
,,.
在 中,
,,
.
在 中,
,,
.
由勾股定理,,即 ,解得 .
米.
18
